ELEKTRIKA (od ἤλεϰτρον »jantar«), 1. nauka o pojavama elektriciteta i njegovoj primjeni; 2. kod jednog diela naših pisaca sinonim za elektricitet.
Članci iz elektrike obrađeni su i podieljeni u tri skupine: I. Elektrika u fizici i kemiji; II. Elektrika u medicini; III. Elektrika u tehnici (elektrotehnika).
I. ELEKTRIKA U FIZICI I KEMIJI: Elektricitet, 683. Elektricitet trenjem, 685. Električka glasba, 685. Električka struja, 685. Električke jedinice, 687. Električki elementi, 690. Električki titraji, 690. Električki valovi, 693. Elektroakustika, 693. Elektro-analiza, 695. Elektrode, 695. Elektrodinamika, 695. Elektrofor, 697. Elektroforeza, 698. Elektrokemija, 698. Elektrokinetički pojavi, 699. Elektrolitička disociacija, 700. Elektrolitička polarizacija, 700. Elektroliza, 700. Elektroluminiscencija, 702. Elektromagnetizam, 702. Elektromagnetska indukcija, 704. Elektromagnetski valovi, 704. Elektrometri, 708. Elektromotorna sila, 708. Elektron, 708. Elektron negativni i pozitivni, 712. Elektron težki, 712. Elektroni i kemijska svojstva elemenata, 712. Elektronska optika, 713. Elektronske cievi, 715. Elektronski mikroskop, 719. Elektronski udarac, 722. Elektronvolt, 723. Elektrooptika, 723. Elektroozmoza, 725. Elektroskopi, 725. Elektrostatika, 725. Elektrostatski strojevi, 727. Elektrostrikcija, 730.
Elektricitet (novolat. electricitas), fizikalni agens, koji prouzrokuje električke pojave. Znanstveno proučavanje fizikalnih pojava počinje s godinom 1600, kad je u Londonu izašlo djelo Gilberta »De magnete magneticisque corporibus«, u kojemu je 2. poglavlje II. knjige posvećeno pojavima na jantaru i nizu drugih tvari, za koje je Gilbert našao da trenjem dobivaju kao i jantar svojstvo, da privlače laka tjelešca. Istina, to svojstvo jantara bilo je poznato već Talesu iz Mileta (oko 600 pr. Kr.), a Teofrast je 300 godina kasnije amo pridodao i linkurion (vjerojatno turmalin). Međutim je to oskudno znanje do Gilbertova vremena prošireno samo tim, da je isto svojstvo nađeno i na ahatu; ali se nazadovalo u osnovi pojava, jer je uobće bilo sporno, treba li jantar trti, da bi dobio svojstvo privlačenja lakih tjelešaca, ili ga u tu svrhu treba ugrijati. Gilbert je svoja iztraživanja izveo s pomoću verzorija, lakoga kovnog štapića duljine 3 do 4 engl. palca, gibljivo poduprtog, po uzoru na magnetsku iglu, u njegovu težištu o jednom šiljku. Tjelesa, koja su trenjem dobila svojstvo, da privlače jedan kraj verzorija, kad ih je njemu primaknuo, nazvao je Gilbert (corpora) electrica prema grčkom nazivu za jantar (ἤλεϰτρον), a mehaničku silu privlačenja vis electrica.
Kroz prvih 150 godina poslije Gilberta vrlo sporo se napredovalo u upoznavanju najosnovnijih pojava elektriciteta. Neki su od njih opažani po više puta, ali su opet i opet pali u zaborav. Električnu influenciju, na kojoj se temeljio već verzorij, odkrili su djelomično najprije Guericke 1663 (1672) pa ponovno Hawksbee (1770), Gray (1729), spoznao ju je u cielom obsegu istom J. Canton (1753), a Wilke ju je 1757 izpravno protumačio. Jedna spoznaja uvjetovala je drugu, nova spoznaja pridoniela je usavršavanju eksperimentalnih sredstava, a ovo je omogućivalo nova odkrića i nove spoznaje. Dok Gilbert zna samo za električko privlačenje, pa čak izričito izključuje mogućnost odbijanja (I, II, c. 39), Guericke je prvi opazio, da njegova sumporna kugla, natrta, odbija laka tjelešca, pošto ih je izprva privukla. Nekako u isto doba našao je to i Boyle; ali na to se zaboravilo. Istom Du Fay je 1734 odkrio, da postoje dvie vrste elektriciteta, koje je on skraćeno nazvao elektricitetom stakla i elektricitetom smole; za njih su se kasnije uobičajili Franklinovi nazivi (1747): pozitivan i negativan elektricitet. Tim je Du Fay našao i prvi kvalitativni zakon, da se istoimeni elektriciteti odbijaju, a raznoimeni privlače. Međutim je Gray četiri godine prije toga podielio tjelesa u vodiče i nevodiče elektriciteta. Sve to omogućilo je konačno odkriće influencije po Cantonu i njezino objašnjenje po Wilkeu.
Posljednje godine prve polovine 18. st. doniele su prvi kvantitativni zakon elektriciteta postavljen od Watsona, a neposredno zatim od Franklina: da na tarilu i na natrtom tielu nastaju jednake množine suprotnih elektriciteta. Točan dokaz ovog zakona donio je tekar Faraday. U isto doba pada odkriće lajdenske boce po Kleistu (listopad 1745) i Musschenbroeku (siečanj 1746). Druga polovina istog stoljeća doniela je prvi brži uzpon u spoznaji električkih pojava. Mnoga odkrića omogućena su izumom prvih elektroskopa i njihovim usavršavanjem (Canton, Henley, Volta, Bennet). Odmah u godinama 1750—52 dolaze Franklinova iztraživanja o olujnom elektricitetu i njegov dokaz, da je munja električna iskra. Cassini je 1752 našao elektricitet u atmosferi i po liepom vremenu. Godine 1785 postavlja Coulomb drugi kvantitativni zakon elektriciteta za silu f, kojom uzajamno djeluju dvie točkaste množine elektriciteta e i e1 u međusobnoj daljini r : sila je f = ± C • e e1/r2. Tim je omogućen put matematičkoj analizi u područje nauke o elektricitetu; nju su amo uveli Laplace, Biot i Poisson. — U isto doba padaju zamašna električka iztraživanja Cavendisha, od kojih je veći dio izašao na vidjelo istom, kad je Maxwell izdao Cavendishova djela (1879). Cavendish je uveo pojmove električkog potenciala i kapaciteta, izveo je prva mjerenja kapaciteta, odkrio je utjecaj okolnog medija na kapacitet vodiča, mjerio je električke vodljivosti čvrstih tjelesa i tekućina. On je dokazao, da se elektricitet nalazi samo na površini vodiča.
Konac 18. st. znači ujedno početak drugog razdoblja u razvoju spoznaje električkih pojava odkrićem najprije t. zv. kontaktnog elektriciteta (Volta, 1796), pa galvanskog članka i električne struje. Odkriće galvanskog članka vezano je uz ime Volte (1800); u stvari već od 1796 Ash, Humboldt, Ritter izvode primitivne pokuse elektrolize, gdje im kao izvor struje služe dvie kovine s vodom ili vlažnim tielom između njih. Odkrićem magnetskog polja električke struje (Oersted, 1820), magnetiziranja čelika u uzvojnici, kroz koju teče struja (Arago i Gay-Lussac, 1820), međusobnog djelovanja paralelnih i antiparalelnih struja (Ampere, 1820) utvrđena je veza između magnetizma i elektriciteta. Magnetizam je po Ampèreovoj teoriji magnetizma (1821, 1822) postao popratnim pojavom struje elektriciteta. Ova je unutrašnja veza između njih produbljena g. 1831 odkrićem induciranih struja po Faradayu. Od ove godine počinje treće razdoblje u razvoju nauke o elektricitetu, a od g. 1867, kad su Werner Siemens i Wheatstone istodobno odkrili t. zv. dinamoelektričko načelo, nadošlo je doba veće tehničke primjene električke struje.
Gilbert je zamišljao, da elektrizirano tielo izpušta neki agens (effluvia), koji prouzrokuje privlačenje okolnih tjelešaca. Sredina 18. st. doniela je prve hipoteze o biti elektriciteta; to su hipoteze električkih fluida. Po starijoj, t. zv. unitarnoj teoriji, koju je postavio Watson, a do ugleda je došla pod Franklinovim imenom, svaka tvar sadržava u sebi neki imponderabilni agens, koji oni zovu električkim fluidom ili električkim eterom. Ako tvar sadržava toliko tog fluida, koliko može da ga primi, a da se on ne nagomila na površini, tvar je u neelektričkom stanju. Ako je sadržaj na fluidu veći od te propisane količine, tvar je pozitivno električna, a negativno je električna, ako je sadržaj na fluidu manji. Da bi se protumačilo međusobno odbijanje negativno električkih tjelesa, sliedilo bi iz ovoga, da tvar po sebi, t. j. tvar, kojoj bi posve bio oduzet električki fluid, odbija drugu tvar, kojoj je također oduzet električki fluid. Tu su vidjeli sukob unitarne teorije s osnovom Newtonove obće gravitacije i nisu nalazili način, kako bi se ova opreka izravnala.
Zbog ove potežkoće je R. Symmer postavio (1759) teoriju dvaju električkih fluida, kojoj začetak imamo već kod Du Faya. Po ovoj, t. zv. dualističkoj teoriji tvar u neutralnom stanju ne pokazuje električkih svojstava, jer sadržava jednake količine dvaju imponderabilnih električkih fluida, pozitivnog i negativnog. Jedno tielo je električki pozitivno ili negativno prema tome, da li je na njemu višak jednog ili drugog fluida. Unitarna teorija je jednostavnija. Ona razlikuje dva prabivstva: tvar i električki fluid; oboje zajedno sačinjavaju neutralnu tvar. Ipak je konačno prevladala dualistička teorija. Ona je dala svoj pečat elektrostatičkoj terminologiji. Premda su pisci gotovo do kraja prošlog stoljeća kod prikazivanja električke struje mislili dualističkom teorijom, ipak pravila i zakoni električke struje i elektrodinamike, koji su postavljeni u prošlom stoljeću, više odgovaraju terminologiji unitarne teorije, ali ne kao izraz takva shvaćanja, nego više kao skraćeni način izražavanja. Pobjedi dualističke teorije uvelike su pridoniele neke eksperimentalne razlike u pojavima s pozitivnim i s negativnim elektricitetom, koje su bile odkrivene upravo u drugoj polovici 18. stoljeća, poimence: razlika pozitivne i negativne slike kod Lichtenbergovih figura, t. zv. Lullinov pokus, te razlike u svjetlostnim pojavima na šiljku s pozitivnim i na šiljku s negativnim e-om.
Teorije fluida bile su usmjerene samo na tumačenje elektrostatičkih pojava, pa nije bilo potrebe zalaziti u hipoteze o biti tih fluida. Ipak nalazimo već kod Franklina misao, da se električki fluid sastoji od vrlo sitnih čestica. Aepinus (1759) čak govori u međusobnom privlačenju između čestica Franklinova električkog fluida i atoma tvari. Tu prvi put susrećemo misao o zrnatoj građi elektriciteta. Ova misao je još onda ostala neplodnom; ali je ponovno oživjela, kad je dobila snažan eksperimentalni oslon u Faradayevim iztraživanjima elektrolize (1833), koja su pokazala, da svaki jednovalentni ion nosi jednaku množinu elektriciteta, te da je obćenito množina elektriciteta, koju nosi jedan ion, točno proporcionalna s njegovom valencijom. Ipak je u idućim godinama nastao zastoj u atomističkom shvaćanju elektriciteta, a uzrok je došao upravo od Faradaya. Jer po Faradayu bit električkih pojava je električko polje; ono se sastoji u deformacijama ili mehaničkim napetostima etera ili okolnog dielektričkog sredstva. Slobodni električki naboji javljaju se na površini vodiča, gdje izviru ili svršavaju električke silnice. Prema teme su pojavi na vodičima nešto sporedno. Tako bi shvaćanje elektriciteta kao substancije, uzporedljive s tvarju, dolazilo u pitanje. Novu snagu dobilo je ovo Faradayevo shvaćanje u Maxwellovoj obradbi (1873), pogotovo kad je Maxwellova teorija ojačana Hertzovim pokusima (1888).
S druge strane je W. Weber upravo u to doba, najprije 1846, pa opet 1871, razvio posve atomističko shvaćanje elektriciteta. On govori o atomima elektriciteta, pozitivnog i negativnog, koji imaju masu, i ako vrlo malenu prema masi atoma tvari. Ti električki atomi mogu biti spojeni s atomima tvari i onda čine s njima cjelinu. Stoney je 1874 iznio shvaćanje, da se elektricitet sastoji od međusobno jednakih najmanjih množina e-a, pa je na osnovu elektrolize i kinetičke teorije plinova procienio tu najmanju električku množinu na 0,3 • 10-10 elst-cgs-jedinica. Edlund (1877) govori o električkim molekulima u kovinama, a Helmholtz (1881) poput Stoneya iznosi zaključak, da su i pozitivni i negativni elektricitet razdieljeni u elementarne množine, koje se vladaju kao atomi elektriciteta. Napokon po Lorentzu (1895) električka struja u kovinama sastoji se u progresivnom gibanju najmanjih jednakih čestica e-a.
Nazivi za ova zrnca elektriciteta, bez obzira na njihov predznak, bili su raznoliki: kod Lorentza to su ioni, kod W. Thomsona elektrioni, kod J. J. Thomsona električke korpuskule. Stoney je (1891) za njih, ne obazirući se na predznak, dao naziv elektron. J. J. Thomson i Kaufmann su dokazali (1897), da su katodne zrake struja najmanjih čestica negativnog elektriciteta s masom odprilike hiljadu puta manjom od mase vodikova iona, a Fitzgerald je iste godine zaključio, da su to slobodni elektroni. Po Lorentzu su ti elektroni identični s nosiocima struje u kovinama.
Po našem današnjem znanju elektricitet se sastoji od elektrona, međusobno jednakih najmanjih množina negativnog elektriciteta. Oni sudjeluju u sastavu atoma tvari. Millikan (1912) je izmjerio metodom lebdećih kapljica množinu elektriciteta, koju ima elektron; našao je vriednost: 4,774 • 10-10 elst-cgs-jedinica. Po novijim mjerenjima bolje odgovara: 4,80 • 10-10 elst-cgs-jedinica. Masa elektrona je okruglo 1850 puta manja od mase protona. Tolman i njegovi suradnici su u nizu pokusa od 1916 do 1926 pokazali, da su zaista elektroni nosioci struje u kovinama.
Čestice, koje bi bile najmanja zrnca pozitivnog elektriciteta, a inače bi u svemu odgovarale elektronu, dosada nisu poznate. U protonu, koji je jezgra vodikova atoma, množina je 4,80 • 10-10 elst-cgs-jedinica pozitivnog elektriciteta vezana uz tvar. Pozitron, koji je masom jednak elektronu, a odgovara množini 4,80/10-10 elst-cgs-jedinica pozitivnog elektriciteta, vrlo je nestalna i kratkovječna čestica, a nema ni podataka, koji bi upućivali na to, da bi on izravno sudjelovao u građi atoma tvari (→ čestice elementarne).M. K.
Elektricitet trenjem. Najstariji način dobivanja slobodnog e-a je elektriziranje trenjem (→ elektricitet). U stvari radi se o odjeljivanju suprotnih e-a, jer se e. jednog predznaka javlja na natrtom tielu, a suprotni e. u jednakoj množini javlja se na tarivu. Du Fay je odkrio (1734), da se i kovine dadu elektrizirati trenjem pomoću zgodnog tariva, ako ih izoliramo. U školskim pokusima obično taremo stakleni štap Kienmayerovim amalgamom, razasutim na koži, ili ebonit taremo krznom. Kod toga staklo pokazuje pozitivan, a ebonit negativan elektricitet. Uostalom, predznak e-a na istom natrtom tielu zavisi u prvom redu o vrsti tariva; osim toga on zavisi o stanju površine tiela i o temperaturi. Gladko staklo pri običnoj temperaturi, natrto kožom, Kienmayerovim amalgamom ili svilom, pokazuje pozitivan, a natrto vunom ili krznom, pokazuje većinom negativan elektricitet.
Ako dva tiela iz različitog materiala dovedemo jakim pritiskom u najuži dodir pa ih opet razmaknemo, oni pokazuju poslije razmicanja suprotne elektricitete. Ovo vriedi i za dodir kovine s izolatorom; na pr. spustimo li sumpornu kuglu u čistu živu pa je izvučemo, sumpor pokazuje negativan, a živa pozitivan elektricitet. To je e. dodirom. Po Helmholtzu dobivanje e-a trenjem svodi se na e. dodirom; uloga trljanja je samo ta, da se na što više mjesta uzpostavi potreban najuži dodir između oba tiela. Za dodir dvaju različitih čvrstih dielektrika ili za dodir čvrstog dielektrika s tekućim vrlo obćenito vriedi Coehnovo pravilo: nakon dodira dvaju dielektrika pokazuje pozitivan e. dielektrik s većom konstantom dielektričnosti (A. Coehn, 1898). Ako staklenu kuglu prevučemo šelakom ili parafinom pa je zaronimo u vodu i izvučemo, šelak ili parafin pokazuju negativan, a voda pozitivan e., jer je konstanta dielektričnosti vode daleko veća od konstante dielektričnosti šelaka ili parafina.
E. trenjem i e. dodirom posljedica su električkog dvosloja na površinama tjelesa. Po Lenardu takav dvosloj posljedica je molekularnih sila i njima izazvane orientacije dipolnih molekula na površini, tako da je negativni kraj dipola na vanjskoj strani. Dovedu li se površine dvaju tiela pritiskanjem mjestimice na daljine molekularnih dimenzija, negativni električki naboji iz površinskog dvosloj a na tielu s većom konstantom dielektričnosti lako prieđu na površinu tiela s manjom konstantom dielektričnosti, pa kad površine razmaknemo, prva pokazuje pozitivan, a druga negativan elektricitet.M. K.
Električka glasba → Elektroakustika 4.
Električka struja je elektricitet u gibanju. Ovom definicijom nije obuhvaćena Maxwellova t. zv. pomačna struja u praznom prostoru, koja se sastoji u vremenskim promjenama električkog polja, premda je i s njom spojena glavna značajka e-e s-e, magnetsko polje (→ Maxwellova teorija). U dielektriku pomačna je struja skopčana s polarizacijom dielektrika. Put, kojim teče energija e-e s-e, zovemo krugom struje. Pomačna struja zatvara sve krugove e-e s-e u zatvorene krugove.
Pod e-om s-om u običnom govoru razumievamo struju elektriciteta kroz kovne vodove. Dana definicija je šira, jer ona osim ove, t. zv. vodne, struje obuhvaća i konvektivnu struju. To je gibanje elektriciteta spojeno s gibanjem tvari kao nosioca električkih naboja. Ovamo idu: ionske struje u plinovima (→ ionizacija), u disociranim tekućinama (→ elektroliza), u čvrstim elektrolitima i struje u dielektričkim tekućinama; ove posljednje sastoje se dielom u strujama iona, dielom u strujanju električki nabijene prašine. Među konvektivne struje idu struja u Rowlandovu pokusu (H. A. Rowland, 1876) i struja u Röntgenovu pokusu (W. C. Röntgen, 1885). Električka iskra je kombinacija konvektivne i pomačne struje.
Uzrok gibanju elektriciteta kod vodnih struja i kod ionskih struja — uključujući amo i struje električki nabijene prašine — razlika je potenciala ili napetost. To je elektromotorna sila u najširem smislu, dok pod elektromotornom silom u užem smislu razumievamo svaki uzrok, koji stvara ili teži da stvori nejednakost gustoće elektrona u vodičima. Taj uzrok mogu biti: razlika temperature na dodirnim mjestima dvaju različitih vodiča ili strma temperaturna nesimetrija na istom vodiču; zatim kemijsko djelovanje na dodirnim plohama dvaju različitih vodiča s elektrolitom, razlika koncentracije iste elektrolitičke raztopine, relativno gibanje vodiča prema magnetskom polju ili promjena magnetskog toka obuhvaćenog krugom vodiča.
Ionske struje sastoje se u gibanju suprotno elektriziranih čestica u suprotnim smjerovima. Gotovo do podkraj prošlog stoljeća slična je slika vladala i o struji u kovnim žicama: smatrali su je strujom suprotnih elektriciteta u suprotnim smjerovima. Uobičajeno označivanje smjera struje u žici od pozitivnog pola izvora napetosti k negativnom polu konvencionalni je način izražavanja. Po Lorentzovoj teoriji (1895, 1904) struja u kovnim žicama je progresivno gibanje elektrona, t. j. negativnog elektriciteta. To su vodni elektroni iz atomskih ljusaka atoma kovine; oni se gibaju nasuprot smjeru napetosti, kako je on konvencionalno definiran, t. j. elektroni se gibaju nasuprot smjeru struje. Zato kovne vodiče zovemo i elektronskim vodičima. Iztraživanja, što su ih izvršili R. C. Tolman i njegovi suradnici od 1916 do 1926, dokazala su, da nosioci struje u kovinama zaista imaju negativni elektricitet, a njihova su mjerenja pokazala s dovoljnom približnošću, da je specifički naboj tih nosilaca jednak specifičkom naboju elektrona. I normalni Hallov efekt upućuje na to, da nosioci struje u kovinama imaju samo negativan predznak. Katodne zrake i struje u visoko evakuiranim elektronskim cievima također su struje slobodnih elektrona.
Jakost struje je množina elektriciteta, koja proteče kroz jedan presjek diela kruga struje u 1 sekundi. Mjerimo je amperima. Struja trajno istog smjera je istosmjerna struja; ako joj je uzto i jakost kroz veće vremenske razmake stalna, zovemo je stalnom strujom. Struja, kojoj se jakost i smjer periodički mienjaju s vremenom, zove se izmjeničnom strujom. Promjenljiva struja, koja se dade razstaviti u stalnu i u izmjeničnu komponentu, zove se složenom strujom. Predmet ovog članka je poglavito stalna struja u kovnim vodičima.
Odkrivanje zakona e-e s-e bilo je omogućeno, kad su se znali uzpostaviti izvori električke napetosti, koji su kroz dulje vremenske razmake stalni. To su najprije bili termočlanci (v.), kojima su oba spojišta bila na stalnim temperaturama; tako je Ohm kod dokazivanja zakona e-e s-e, nazvanog njegovim imenom, upotrebljavao kao izvor napetosti termočlanke od bizmuta i bakra, kojima je jedno spojište bilo na temperaturi 0°C, a drugo spojište na temperaturi 100°C. Od 1836 (Daniellov članak) upotrebljavali su se u tu svrhu i stalni galvanski članci.
Osnovni zakon e-e s-e je Ohmov zakon (1827). Po tom je zakonu jakost struje (i) proporcionalna s elektromotornom silom u krugu ili napetošću na kraju žice (V), a obrnuto je proporcionalna s električkim odporom (r) u krugu, t. j. i = V/r. Taj zakon vriedi i za dielove žice između točaka A i B; ako sa VA-VB označimo napetost između A i B, a sa rAB odpor diela žice između njih, onda
je i = VA-VB/rAB. Veličina r u nazivniku Ohmova zakona, koju zovemo električkim odporom žice, ima u zadanom krugu struje pri stalnoj temperaturi žice stalnu vriednost r = V/i. Za razliku od drugih veličina, koje u najobćenitijem slučaju ograničuju jakost izmjenične struje, zovemo ga i omskim odporom. Ohmov zakon vriedi i za efektivna jakost izmjenične struje tehničke frekvencije u krugu, koji sadržava samo omski odpor, ako se u brojniku stavi efektivna napetost.
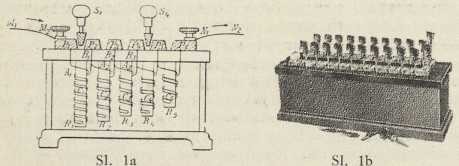 Odpornik s čepovima
Odpornik s čepovimaOmski odpor jedne žice stalnog presjeka q zadan je zakonom odpora: r = γl/q, gdje je l dužina žice. Jedinica odpora je 1 om, Faktor γ je materialna konstanta tvari žice, t. zv. specifički električki odpor. To je odpor komada te tvari dužine 1 cm, presjeka 1 cm2. Mjeri se jedinicom om.cm. Da bi se izbjegli maleni brojevi, u praksi se uzima kao specifički odpor 104 puta veća vriednost, t. j. odpor žice dužine 1 m, presjeka 1 mm2. Najmanji specifički odpor imaju srebro (104γ = 0,016 om.cm) i bakra (104γ = 0,017 om.cm). Odpor se najpouzdanije mjeri metodom Wheatstoneova mosta (v.). Obrnuta vriednost 1/γ = k zove se električkom vodljivošću; mjeri se jedinicom om -1 • cm-1. Između električke vodljivosti i toplinske vodljivosti čistih kovina postoji jednostavan snošaj: one su međusobno proporcionalne (Wiedemannov i Franzov zakon, 1853). Specifička vodljivost najboljih izolatora je prosječno 1023 puta manja od specifičke vodljivosti kovina.
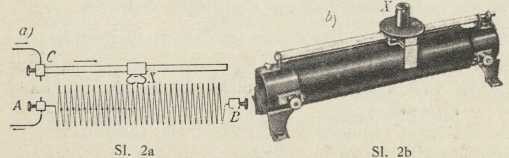 Odpornik s pomicaljkom
Odpornik s pomicaljkomSpecifički električki odpor mienja se s temperaturom žice: kod kovina raste s temperaturom, a kod ugljena (osim najčišćeg grafita), silicija i još nekih tvari opada s porastom temperature. Zato redovito dajemo njegovu vriednost za 18°C. U manjim temperaturnim razmacima dade se prikazati sa: γ = γ0 • [1 + β (t — t0)], gdje γ0 i t0 znače početni specifički odpor i početnu temperaturu; β je termički koeficient odpora. Električka vodljivost elektrolita dana je stupnjem disociacije; a kako disociacija raste s temperaturom, β je kod elektrolita negativan. Kod kovina se električki odpor ponešto mienja i s tlakom, te se, osim kod litija, bizmuta i antimona, obćenito umanjuje, kad tlak raste. Tlačni koeficient odpora, t. j. promjena odpora kod povećanja tlaka za 1 at, jest 3000 do 4000 puta manji od termičkog koeficienta. Odpor kovina se povećava u magnetskom polju; najviše se povećava odpor bizmuta. Odpor sive ili kovne modifikacije selena i odpor talijeva lako oksidiranog sulfida umanjuju se, ako na njih pada svjetlost. To je posljedica unutrašnjeg fotoelektričkog efekta (v.). Odpor nekih kovina, kovinskih slitina i spojeva kod najnižih temperatura naglo pada na nemjerljivo malenu vriednost (→ supravodljivost).
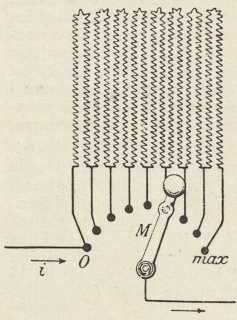 Sl. 3. Shema odpornika s ručkom
Sl. 3. Shema odpornika s ručkomZa reguliranje jakosti struje služe odpornici. Oni su ili odpornici s čepovima (sl. 1a i b) ili odpornici s pomicaljkom (sl. 2a i b) ili odpornici s ručkom (sl. 3). Svaki odpornik ima određenu maksimalnu jakost struje, do koje se smije upotrebiti. Odpornik s čepovima sastoji se od 1 ili 2 izprekidane debele mjedene pruge, koje su na mjestima prekida premoštene po jednom bifilarno namotanom uzvojnicom poznatog odpora u omima. Utisnemo li u rupicu na jednom prekidu pripadni točno izrađeni konički kovni čepić, odpor uzvojnice je izključen. Uzvojnice su od posebnih slitina s malenim termičkim koeficientom odpora (manganin, konstantan, argentan). Ovi se odpornici upotrebljavaju u strogo znanstvenim iztraživanjima. Odporna žica je kod drugih odpornika, koji služe za obične potrebe, od jeftiniiih slitina. Za stalne velike odpore uz malena obterećenja upotrebljava se silit, jedna smjesa silicija i silicijeva karbida s vrlo velikim specifičnim odporom (oko 18000 om.cm).
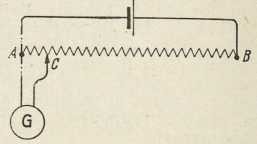 sl. 4. Potenciometarski spoj
sl. 4. Potenciometarski spojMeđu dvjema točkama kovnog vodiča, koji ne sadržava nikakva izvora elektromotorne sile, a kroz koji teče struja, napetost opada (Ohm, 1827). Pad napetosti je proporcionalan s odporom, i to je prema Ohmovu zakonu: V = ir. Dakle napetost jednoliko opada uzduž homogenog vodiča stalnog presjeka. Na tome se osniva potenciometarski spoj, pomoću kojega iz dane napetosti možemo uzeti po volji malenu napetost. U sl. 4 struja iz izvora napetosti teče kroz odpornik AB s pomicaljkom. Onda kroz mjerači instrument G, koji je spojen između kraja A i pomicaljke C, teče struja, kojoj jakost odgovara malenoj napetosti VA-VC.
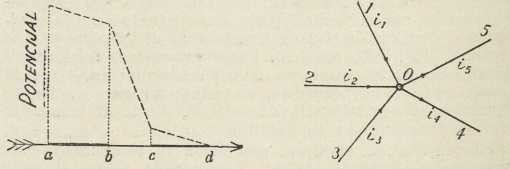 Sl. 5. i Sl. 6.
Sl. 5. i Sl. 6.Sl. 5 prikazuje način opadanja napetosti u nehomogenom vodiču, gdje je između dviju žica ab i cd s malenim odporom uklopljen komad žice bc s velikim odporom. Tako se u vodu s uklopljenom žaruljom praktički cieli pad napetosti nalazi na niti žarulje.
Struja zagrijava žicu, kroz koju teče. Zakon o množini topline, razvijene strujom, našao je Joule eksperimentalnim putem (1841). Množina topline Q (»Jouleova toplina«), razvijena u t sekunda u žici odpora r od struje jakosti i, iznosi: Q = i2rt džaula = 0,24 i2rt gcal. Pomoću Ohmova zakona možemo prvu jednačbu pisati i ovako: Q = iVt džaula. Produkt W = iVt džaula je ujedno energija struje, koja se dade pretvoriti i u druge oblike, na pr. u kemijsku energiju ili u mehaničku radnju. Produkt N =W/t = iV vata je snaga struje.
Kirchhoff je 1847 postavio zakone o struji u razgranjenim vodičima. Prvi Kirchhoffov zakon odnosi se na točku, u kojoj se struja razgranjuje (sl. 6). Dade li se strujama, koje teku prema čvorištu O, pozitivan, a suprotnim strujama negativan predznak, onda je: i1 + i2 + i3 + .... + in = in = 0. Prema tome ni u jednom dielu kruga struje ne može doći ni do nagomilavanja ni do manjka elektriciteta.
Drugi Kirchhoffov zakon odnosi se na zatvorenu petlju vodiča s odporima r1, r2, r3, ...., koja može sadržavati i neke elektromotorne sile Em; u čvorištima A, B, C, .... neka struje bilo kako pritječu ili odtječu (sl. 7). Računajući struje in u petlji, koje teku smjerom kazala na uri pozitivno, a one protivnog smjera negativno, vriedi onda.
inrn = Em. Ako u petlji nema elektromotornih sila, onda je: inrn = 0. Odatle izlazi za n odpora spojenih paralelno između dviju istih točaka: i1r1 = i2r2 = i3r3 = = ...... Za ukupni odpor r sustava tako spojenih odpora izlazi odatle: 1/r = 1/rn. Spojimo li paralelno sa spojkama mjeraćeg instrumenta jedan odpor, koji je k puta manji od odpora instrumenta, onda ovim možemo mjeriti struje (k + 1) puta jače od područja jakosti, za koje je on određen; kroz instrument teče tada jakost i, a kroz paralelni ogranak jakost ki.
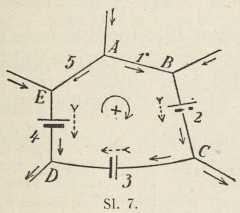 Sl. 7.
Sl. 7.S e-om s-om nerazdvojno je spojeno magnetsko polje struje (→ elektromagnetizam). Brzina, kojom struja izgrađuje svoje magnetsko polje, zavisi o geometrijskom obliku i veličini kruga struje te o magnetskim svojstvima sredstva, u kome leži krug struje. Zato struja ne postigne svoju konačnu jakost, koja joj pripada po Ohmovu zakonu, trenutačno u času uklapanja, već proteče neko, redovito maleno vrieme. U to potrošena energija je magnetskog oblika i zove se unutrašnjom energijom kruga struje. Isto tako magnetsko polje kruga struje ne izčezava trenutačno u času razklopa. Ako je L koeficient samoindukcije (v.) kruga struje, mjeren u henrima, a jakost i struje je mjerena u amperima, onda je unutrašnja energija W=½Li2 džaula.
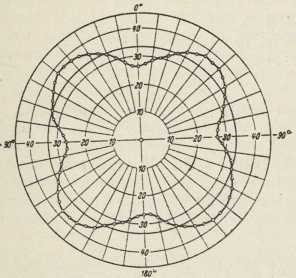 Sl. 8. Polarni diagram promjene električkog odpora
Sl. 8. Polarni diagram promjene električkog odpora
volframova jednokristala u zavisnosti
o položaju magnetskog polja (H=18100 ersteda)
prema glavnoj ravnini kristalne mreže kod 4,220K
(E. Justi, 1941)Za mnoga pitanja dovoljno je kovnu žicu krupno predočiti kao posudu neprodušnih stiena izpunjenu slobodnim elektronima, koji su u živom gibanju podjednako usmjerenom u svim smjerovima. Stavimo li neku električku napetost između krajeva žice, u nesređenom gibanju elektrona pretegne komponenta gibanja protiv smjera napetosti. Brzine ovoga gibanja elektrona protiv smjera napetosti u žici vrlo su malene; na pr. ako je na krajevima bakrene žice presjeka 1 mm2, a dužine 10 m, napetost 1 volt, izlazi za prosječnu brzinu elektrona 0,04 cm/sec. Međutim se djelovanje struje širi brzinom svjetlosti. Djelovanje Coulombovih sila kovinskih iona na elektrone i srazovi ovih s njima očituju se kao električki odpor, a energija, izgubljena u tome, kao Jouleova toplina.
Kod ionskih struja u plinovima i u slabo vodljivim tekućinama Ohmov zakon vriedi samo u jednom uzkom području nižih napetosti. Kod daljeg podizanja napetosti porast jakosti struje zaostaje za porastom napetosti, a kod nešto viših napetosti nastaje pojav zasićenosti, gdje jakost struje ostaje stalna i nezavisna o napetosti; to je onda, kad u svakom djeliću vremena svi razpoloživi ionski parovi stignu na elektrode. Zbog golemog množtva vodnih elektrona u 1 cm3 kovine pojavi zasićenosti ne dadu se opaziti kod običnih gustoća vodne struje u žicama. Bridgman (1922) je na izvanredno tankim slojevima nekih kovina kod vrlo velikih gustoća struje i/q =5.106 ampera/cm2 našao jakosti struje za prosječno 1% manje, nego bi trebale biti po Ohmovu zakonu.
Kroz posljednjih 15 godina iztraživane su promjene električkog odpora različitih kovina, osobito kovinskih jednokristala, u vrlo jakim magnetskim poljima kod vrlo nizkih (tekući dušik) i kod najnižih temperatura (tekući helij). Uzpoređivanje dobivenih rezultata s onima kod obične temperature pokazalo je, da kod obične temperature uvelike utječe na gibanje vodnih elektrona u kovinama toplinsko titranje iona u kristalnoj mreži. Kod temperature tekućeg helija prestaje titranje kristalne mreže, pa promjene odpora u zavisnosti o pravcu magnetskog polja pokazuju, da se elektroni lakše gibaju u nekim ravninama kristalne mreže nego u drugima. To se očituje time, što je električki odpor jednokristala u jakome magnetskom polju manji u pravcu tih prvih ravnina nego u pravcu drugih ravnina (sl. 8; → električke jedinice).M. K.
Električke jedinice u širem su smislu jedinice, kojima se mjere električke i magnetske veličine, kao jakost električke struje, električki napon, električki odpor, tok magnetske indukcije, permeabilnost i t. d. Za svaku od ovih veličina mogla bi se definirati samostalna jedinica. Uzmimo na pr., da jedinice za prve tri veličine odaberemo ovako: električka struja l raztvori u jednoj sekundi jedan miligram vode, električki napon l vlada među polovima olovnog akumulatora, električki odpor stupca žive dugog 10 cm i presjeka 1 mm2 iznosi 1. — Ohmov zakon, koji veže te tri veličine, uz taj izbor jedinica glasi: Ri :U = k = 2,0, gdje su R, i, U mjerni brojevi odpora, struje i napona. Budući da napisana veza vriedi bez obzira, od čega je žica, kakav ima oblik i koju temperaturu, te kako je jaka struja, iznos broja k na desnoj strani ovisi samo o veličini odabranih jedinica za odpor, jakost struje i napon. Ovako napisan Ohmov zakon ima posebni, odabranim jedinicama prilagođeni oblik. — Takvo se razmatranje može nadovezati na bilo koju jednačbu, koja povezuje elektromagnetske (elmg) veličine. Ako je napišemo tako, da je prilagođena nekome naročitom izboru e-ih j-a, tad je to posebna elmg jednačba.
Teorija elektromagnetizma može se razviti bez obzira na jedinice, kojima se imaju mjeriti elmg veličine. U tom slučaju pišu se osnovne elmg jednačbe tako, da se u njima stavi brojčani faktor k = 1. Te elmg jednačbe i iz njih izvedene zovu se obćima za razliku od posebnih. U nekim izvedenim obćim elmg jednačbama dolaze brojčani faktori, na pr. ½, 4π, ..., kao posljedica pri njihovu izvodu provedenih računskih operacija. Tako na pr. u obćem obliku pisan električki Coulombov zakon, koji daje silu F, kojom točkasti električki naboji e1 i e2, djeluju jedan na drugi,
\(\qquad\qquad\displaystyle F=\cfrac{e_1\;e_2}{4\pi\;\varepsilon\;r^2}\)
sadržava brojčani faktor 4π (r je razmak među nabojima, a ε dielektrička konstanta sredstva, kroz koje djeluju naboji). Za obće elmg jednačbe još se kaže da su racionalnog ili Lorentz-Heavisideova oblika.
E. j. čine sustav, ako su brojčani faktori, koje treba staviti u obće elmg jednačbe, da se prilagode tim jedinicama, malobrojni i jednostavni. Sustavi e-ih j-a mogu se prema poviestnom razvoju označiti kao absolutni, empirički i moderni.
1. ABSOLUTNI SUSTAVI ELEKTRIČKIH JEDINICA.
a) Elektrostatski (elst) cgs sustav uzima kao osnovne jedinice: za dužinu centimetar, za masu gram, za vrieme sekundu i za dielektričku konstantu — dielektričku konstantu praznoga prostora, dakle: cm, g, sek, Ke, gdje smo s Ke obilježili odabranu jedinicu za dielektričku konstantu, jer nema posebnog imena. Sve ostale elst cgs jedinice izvode se iz ove četiri osnovne. Pritom se služimo elmg jednačbama t. zv. običnog oblika, koje se od obćih (racionalnih) elmg jednačbi razlikuju u položaju brojčanog faktora 4π. (Ovo premještanje brojčanog faktora 4π iz jednih jednačbi u druge jest prilagođivanje obćih jednačbi odabranim jedinicama.)
Elst cgs jedinica električkog naboja definira se pomoću električkog Coulombova zakona napisanog u običnom obliku:
\(\qquad\qquad\displaystyle F=\cfrac{e_1\;e_2}{\varepsilon\;r^2}.\qquad\qquad\)(1)
Naime silu F mjerimo cgs jedinicom za silu, din, razmak r centimetrom, dielektričku konstantu ε elst cgs jedinicom Ke. Elst cgs jedinica za električki naboj Qe odabira se tako, da mjerni brojevi naboja e1 i e2 u toj jedinici i mjerni brojevi veličina F, r, ε, u spomenutim jedinicama, uvršteni u jednačbu (1) na mjesto odnosnih veličina, zadovolje tu jednačbu. Prema tome električki naboj 1 Qe odbija isto takav u daljini 1 cm kroz prazni prostor (ε = ε0 = 1Ke) silom 1 din. Definiciju jedinice Qe možemo simbolički pisati
\(\qquad\qquad\displaystyle \text{din}=\cfrac{{\rm Q}_e\cdot{\rm Q}_e}{{\rm K}_e\cdot{\rm cm}^2}.\)
Iz gornje definicije izlazi ova oznaka
Qe = cm3/2 • g½ • sek-1 • Ke½
(→ dimenzije u fizici, → din).
Električka struja u žici ima jakost 1 elst cgs jedinicu (1 Ie), ako presjekom žice prođe u 1 sek električki naboj 1 Qe. Dakle Ie = Qe • sek-1.
Elst cgs jedinica za magnetski naboj (jakost magnetskog pola) definira se jednačbom za silu F, kojom kružna električka struja jakosti i djeluje na magnetski naboj m u središtu kruga:
\(\qquad\qquad\displaystyle F=2\pi\;\cfrac{i\;m}{r},\qquad\qquad\)(2)
gdje je r polumjer kružnice, kojom teče električka struja. Točkasti magnetski naboj iznosi 1 elst cgs jedinicu, ako u središtu kružnice polumjera 1 cm djeluje na njega sila 2π din, kad kružnicom (koja je od žice) teče struja jaka 1 Ie.
Točkasti magnetski naboji m1 i m2 djeluju jedan na drugi silom F, koja je dana magnetskim Coulombovim zakonom:
\(\qquad\qquad\displaystyle F=\cfrac{m_1\;m_2}{\mu\;r^2},\qquad\qquad\)(3)
gdje je r razmak magnetskih naboja, a u permeabilnost sredstva, koje te naboje okružuje. Tim je zakonom definirana elst cgs jedinica Me, kojom se mjeri permeabilnost. Ono bi sredstvo imalo permeabilnost 1 Me, u kojem bi dva jedinična magnetska naboja (u elst cgs mjeri), u razmaku 1 cm, djelovala jedan na drugi silom 1 din.
Sredstva s golemom permeabilnosti μ = 1 Me nema. Po Maxwellovoj teoriji jest brzina elmg valova u izolatoru
\(\qquad\qquad\displaystyle v=\cfrac1{\sqrt{\varepsilon\;\mu}},\qquad\qquad\)(4)
gdje je ε dielektrička konstanta, a μ permeabilnost izolatora. Za prazni prostor tim je izrazom dana i brzina svjetlosti
\(\qquad\qquad\displaystyle c=\cfrac1{\sqrt{\varepsilon_0\;\mu_0}}=\cfrac1{\sqrt{1\,{\rm K}_e\cdot\mu_0}}=2{\rm ,}998\cdot10^{10}{{\rm cm}\over{\rm sek}}=a{{\rm cm}\over{\rm sek}}.\)
Ovdje je μ0 permeabilnost praznog prostora izražena jedinicom Me, a mjerni broj brzine svjetlosti u cm/sek označen je s a, t. j. a = 2,998.1010. Iz posljednjeg izraza sliedi
μ0 = 1/a2cm-2 • sek2 • Ke-1 = 1/a2 Me.
Prema tome je mjerni broj permeabilnosti praznog prostora, izražen u Me, vrlo sitan, jer je a golemo. Iz magnetskog Coulombova zakona (3) sliedi, da bi u praznom prostoru magnetski naboj 1 elst cgs jedinica odbijao isto takav u daljini 1 cm silom a2din≈9.1020 din, a ta je sila nešto veća od težine tereta od 900 bilijuna kilograma.
Definicije ostalih elst cgs jedinica mogu se nadovezati na cgs jedinicu radnje erg. Napon 1 elst cgs jedinica (1 Ve) vlada između dva mjesta električkog polja, ako pri prienosu električkog naboja 1 Qe s jednog mjesta na drugo dobijemo odnosno potrošimo radnju 1 erg. Dakle Ve = cm½ • g½ • sek-1 • Ke-½. Najpoznatija je elst cgs jedinica kapaciteta: Ce. Kondenzator ima kapacitet 1 Ce, ako se električki napon među njegovim pločama promieni za 1 Ve, kad prenesemo električki naboj 1 Qe s jednog obloga na drugi. Odatle oznaka Ce = cm • Ke.
b) Elektromagnetski cgs sustav uzima kao osnovne jedinice: za dužinu centimetar, za masu gram, za vrieme sekundu i za permeabilnost — permeabilnost praznog prostora (Mm).
Slied definicija izvedenih jedinica obrnut je prema onome u elst cgs sustavu i počinje definicijom elmg cgs jedinice za magnetski naboj pomoću magnetskog Coulombova zakona (3). Iz (2) zatim sliedi definicija elmg cgs jedinice Im za jakost električke struje. Elmg cgs jedinica Qm za električki naboj definira se kao naboj, što ga prenese električka struja jaka 1 Im u 1 sek. Iz električkog Coulombova zakona (1) sliedi definicija elmg cgs jedinice Km za dielektričku konstantu.
Definicije ostalih elmg cgs jedinica mogu se nadovezati na cgs jedinicu radnje erg. Najpoznatije elmg cgs jedinice jesu: ersted za jakost magnetskog polja, gaus za magnetsku indukciju i maksvel za tok magnetske indukcije. — U središtu kruga, kojim teče električka struja jakosti 1 Im, jakost je magnetskog polja 2π ersted, ako je polumjer kruga 1 cm, bez obzira, kakvim je jednoličnim sredstvom struja okružena. — U daljini 1 cm od točkastog magnetskog naboja 1 elmg cgs jedinica jest magnetska indukcija 1 gaus, bez obzira, kakvim je jednoličnim sredstvom taj naboj okružen. — Kroz površinu 1 cm2, okomitu na smjer magnetske indukcije veličine 1 gaus, tok je 1 maksvel.
Budući da opet vriedi jednačba (4), koja daje brzinu elmg valova u izolatoru, to za brzinu svjetlosti c ovdje imamo
\(\qquad\qquad\displaystyle c=\cfrac1{\sqrt{\varepsilon_0\cdot1\,{\rm M}_m}}=a{{\rm cm}\over{\rm sek}}.\)
Ovdje je ε0 dielektrička konstanta praznog prostora izražena jedinicom Km. Odatle sliedi ε0 =1/a2 cm-2 • sek2 • Mm-1 = 1/a2Km. Prema tome je mjerni broj dielektričke konstante praznog prostora, izražene u Km, vrlo sitan. Iz električkog Coulombova zakona (1) sliedi, da bi u praznom prostoru električki naboj 1 Qm odbijao isto takav u daljini 1 cm golemom silom a2 din.
Dielektrička konstanta praznog prostora ε0 jest u elst cgs sustavu 1 Ke, a u elmg cgs sustavu 1/a2Km. Dakle
1 Ke = 1/a2Km, ili Km = a2Ke.
Prema tome možemo zamisliti, da elmg cgs sustav nastaje iz elst cgs sustava, ako jedinicu dielektričke konstante povećamo a2 puta, a ostale osnovne jedinice (cm, g, sek) ostavimo nepromienjene. Iz oznaka elst cgs jedinica, koje su jednako građene kao i dimenzijski izrazi, sliedi neposredno
Qm = aQe Im = a Ie Mm = 1/a2Me Cm = 1/aVe Cm = a2 Ce, i t. d.
Prema tome izmjeriti bilo koju električku ili magnetsku veličinu i elst cgs jedinicom i elmg cgs jedinicom jest isto, što i odrediti mjerni broj a brzine svjetlosti u praznome prostoru izražene jedinicom cm/sek (mjerenja Webera i Kohlrauscha, 1856).
c) Miešani sustav električkih cgs jedinica jest onaj, u kojemu se sve električke veličine (dielektrička konstanta, električki naboj, jakost električke struje, odpor, kapacitet, ...) mjere elst cgs jedinicama, a magnetske veličine (permeabilnost, magnetski naboj, indukcioni koeficient....) elmg cgs jedinicama. Mjerni broj brzine svjetlosti a jest brojčani faktor, kojim su elmg jednačbe među veličinama obiju vrsta prilagođene ovom izboru jedinica. Tako na pr. zakon inducirane elektromotorne sile ima ovdje ovaj oblik
U = 1/a∙∆Φ/∆t,
jer za U valja staviti mjerni broj inducirane elektromotorne sile mjerene elst cgs jedinicom za električki napon, dok se promjena toka magnetske indukcije ∆Φ u vremenu ∆t mjeri elmg cgs jedinicom maksvel/sek.
Miešani cgs sustav upotrebili su u svojim razpravama Helmholtz i Hertz. U teoretskoj fizici održao se do danas. Naziva se i Gaussovim sustavom.
Služimo li se pri definiciji elst odnosno elmg cgs jedinica obćim elmg jednačbama, t. j. jednačbama racionalnog oblika, tad se tako dobivene e. j. razlikuju od običnih, o kojima je bilo dosada govora. Miešani sustav racionalnih cgs jedinica upotrebio je Lorentz.
Redovito se još upotrebljavaju oznake izvedenih elst odnosno elmg cgs jedinica bez Ke odnosno bez Mm. Na pr. Qe = cm3/2 • g½ • sek-1, Ce = cm i t. d.
d) Absolutni praktični sustav ima ove osnovne jedinice: za dužinu kvadrant = 109 cm, za masu jedinicu = 10-11 gram, za vrieme sekundu i za permeabilnost — permeabilnost praznog prostora. Jedinica dužine kvadrant dobila je svoje ime odatle, što je malone točno jednaka četvrtini zemaljskog meridiana. Mnoge e. j. ovoga sustava imaju prikladnu veličinu za elektrotehničku praksu i dobile su naročita imena. Pomoću dimenzijskih izraza sliedi ovaj odnošaj između absolutnih praktičnih i elmg cgs jedinica:
| za električki naboj |
1 abs kulon |
= 10-1 elmg cgs jedinica |
| „ električku struju |
1 abs amper |
= 10-1 „„ |
| „ električki napon |
1 abs volt |
= 108„ |
| „ električki odpor |
1 abs om |
= 109„„ |
| „ kapacitet |
1 abs farad |
= 10-9 „„ |
| „ indukc. koeficient |
1 abs henri |
= 109„„ |
| |
1 abs džaul |
= 107 erg |
Ostale se praktične jedinice, izvedene pomoću elmg jednačbi, pisanih na običan način, ne upotrebljavaju.
2. EMPIRIČKI SUSTAVI ELEKTRIČKIH JEDINICA.
Definicije abs praktičnih jedinica smatrale su se odviše abstraktnima za praksu, za koju su bile zamišljene. Zato su međunarodnim dogovorom utvrđeni praksi pristupačniji propisi, kojima se imaju ostvariti praktične jedinice. Ovako definirane praktične jedinice zovu se, za razliku od absolutnih, međunarodnima (int).
Prvi su propisi dogovoreni na međunarodnom sastanku elektrotehničara u Chicagu (1893). — Jedinicu električkog odpora int om ima stupac žice dug 106,3 cm i jednoličnog presjeka 1 mm2, pri temperaturi leda, koji se tali. — Jedinicu jakosti električke struje int amper ima stalna električka struja, koja iz vodene raztopine srebrnog nitrata izluči 1,118 mg srebra u sekundi. — Ti su brojevi odabrani tako, da se, prema ondašnjem stanju električkih mjerenja, postigne što bolje poklapanje int i abs praktičnih jedinica. Pošto je definirana jedinica električkog odpora i jedinica jakosti električke struje, to onda pomoću Ohmova zakona sliedi definicija jedinice električkog napona, u ovom slučaju int volt. Za praksu je međutim važno, da se i int volt ostvari neposredno naponom nekog normalnog galvanskog članka. Na sastanku u Chicagu uzet je Clarkov članak kao normalan, i dogovoreno je, kolikim će se smatrati njegov napon mjeren u int voltima. Domala se pokazalo, da je Clarkovim člankom određen volt osjetljivo veći od int volta određenog int omom i int amperom.
Na međunarodnom kongresu u Londonu (1908) zaključeno je, da se imaju smatrati int om i int amper kao osnovne međunarodne jedinice. Zatim su propisi za ostvarenje tih jedinica promienjeni utoliko, što je u definiciji int oma broj 106,3 nadomješten brojem 106-300, a zahtjev, da površina presjeka stupca žive bude 1 mm2, zahtjevom, da živa, sadržana u stupcu dužine 106∙300 cm i jednoličnog presjeka, ima masu 14,4521 gram; u definiciji int ampera broj 1,118 nadomješten je brojem 1,11800. Ove su se promjene provele zato, jer su se preciznim mjeraćim metodama mogle mjeriti električke veličine na više znamenaka, nego što su ih imali brojevi dogovoreni u Chicagu. Zatim je zaključeno, da će se Westonov članak (→ članak električki) upotrebljavati kao normalan, i, na osnovu ondašnjih mjerenja, njegov je napon pri 20°C ustanovljen sa 1,0184 int volt. Međutim god. 1910 ta je vriednost popravljena na 1,0183 int volt.
Kasnijim se mjerenjima ustanovilo, da je int om nešto veći od abs oma, a int amper malo manji od abs ampera. Prema današnjem (1944) stanju mjerenja
1 int om = 1.0005 abs om
1 int amp = (1 — 0.0001) abs amp.
Iz osnovnih međunarodnih jedinica int om i int amper izvode se int volt, int kulon, int farad, int henri, int vat, int džaul. Električki napon 1 int volt vlada među krajevima odpora 1 int om, kad njime teče stalna električka struja, jaka 1 int amper. — Električki naboj 1 int kulon prođe u 1 sekundi presjekom žice, kad njome teče stalna električka struja, jaka 1 int amper. — Kondenzator ima kapacitet 1 int farad, ako se električki napon među njegovim oblozima promieni za 1 int volt, kad naboj 1 int kulon prieđe s jednog obloga na drugi. — Samoindukciju 1 int henri ima vodič, u kojem sc inducira elektromotorna sila 1 int volt, kad se struja u vodiču mienja brzinom 1 int amp/sek. — U vodiču se troši električka snaga 1 int vat, kad vodičem teče stalna električka struja, jaka 1 int amper, a među njegovim krajevima. vlada napon 1 int volt; tad se izvrši u 1 sekundi radnja 1 int džaul.
Stariji elektrotehnički sustav e-ih j-a služi se netom navedenim praktičnim jedinicama, a uz ove upotrebljava i ove abs elmg cgs jedinice: Mm za permeabilnost, ersted za jakost magnetskog polja, gaus za magnetsku indukciju i maksvel za tok magnetske indukcije; dielektrička konstanta se mjeri abs. elst cgs jedinicom. Prema tome je ovaj sustav miešan. Elmg jednačbe, prilagođene ovom izboru jedinica, pišu se s takvim brojčanim faktorima, kao da se int praktične jedinice podudaraju s abs praktičnima, jer je prije navedena razlika za praksu bezznačajna. Tako na pr. zakon inducirane elektromotorne sile ima ovdje ovaj oblik
U = 10-8∆Φ/∆t,
jer za U valja staviti mjerni broj inducirane elektromotorne sile mjerene u voltima, dok za kvocient nadesno mjerni broj brzine, kojom se mienja tok magnetske indukcije mjerene elmg cgs jedinicom maksvel/sek.
Noviji elektrotehnički sustav uzima kao osnovne jedinice int om, int amper, sekundu i za dužinu centimetar ili metar. Pri definiciji izvedenih jedinica služi se obćim (racionalnim) elmg jednačbama, a zahtieva se, da u ove ne pridođe nikakav novi brojčani faktor. Tako se na pr. jedinica jakosti magnetskog polja definira izrazom, koji daje jakost magnetskog polja H u dugoj, jednolično namotanoj uzvojnici
H = in/l,
gdje je i jakost struje u uzvojnici, n broj zavoja, a l dužina uzvojnice. Budući da ovdje i mjerimo amperom, l centimetrom odnosno metrom, to onda sliedi, da H valja mjeriti jedinicom amp/cm odnosno amp/met (ili amp. zavoj/cm odnosno ampzavoj/met). U ovom je sustavu jedinica mase izvedena jedinica. Može se izvesti na pr. iz izraza, koji daje snagu stalne električke struje. Ako je cm jedinica dužine, tad je elektrotehnička jedinica mase
\(\qquad\qquad\displaystyle 1\;{{\rm int\;om\cdot int\;amp^2\cdot sek^3}\over{\rm cm^2}}=10003\;{\rm kg}.\)
dakle malo veća od 10 tona.
U praksi se upotrebljavaju i jedinice izvan sustava. Tako se snaga motora mjeri u kilovatima (1 kilovat = 1000 vat), a električka energija prodaje se na kilovat-sate (kilovat-sat jest radnja, što je izvrši motor, kad radi snagom 1 kilovat u 1 satu). Slabe se struje mjere u miliamperima i mikroamperima, a visoki naponi u kilovoltima, kapaciteti u mikrofaradima i pikofaradima; naboj, koji prođe elek. člankom, u ampersatima (naboj 1 ampersat prođe presjekom vodiča u 1 sat, ako njima teče stalna elek. struja 1 amper).
Napomena. Izvršni organ međunarodne metarske konvencije Glavni savjet za mjere i uteze zaključio je g. 1933 na priedlog njemu podređenog Odbora za mjere i uteze, da se imaju uvesti namjesto međunarodnih praktičnih jedinica absolutne praktične. Istodobno je ovlastio spomenuti odbor, da odredi dan, kad ima ta promjena nastupiti. Taj je zaključak obvezan za sve države, koje su pristupile metarskoj konvenciji. Odbor za mjere i uteze zaključio je g. 1935, da se 1. siečnja 1940 ima prieći na absolutne jedinice. U tom je smislu trebalo promieniti zakone o e-im j-ama izdane u državama metarske konvencije. Nastali rat spriečio je, da se provede ta promjena, pak su još i danas (1945) u kreposti međunarodne praktične jedinice. Međutim, s obzirom na dobro poklapanje međunarodnih praktičnih jedinica s absolutnima ta bi promjena bila za obična električka mjerenja bez ikakvih posljedica. Razlike bi se opazile tek kod mjeraćih metoda s pogrješkom manjom od 1‰.
Za praksu međutim treba ostvariti te jedinice zgodnim normalama. Prema današnjem stanju mjerenja ima stupac žive, dug 106∙250 cm, mase 14,4453 gram, i jednoličnog presjeka, pri 0°C odpor 1 abs om. Abs amper izluči u sekundi 1,11815 mg srebra. Westonov članak ima napon 1.01865 abs volt. — Nije toliko znatna razlika u veličini tih brojeva prema onima, kojima su definirane int praktične jedinice, koliko u njihovu značaju. Stari su brojevi dio definicije, pa zato nepromjenljivi, a ovi rezultati mjerenja, i popravljat će se, kako bude napredovala tehnika mjerenja.
3. MODERNI SUSTAVI JEDINICA.
Ovi su sustavi zamišljeni tako, da im pripadaju praktične električke jedinice, a mehaničke (za silu, masu,...) imaju zgodnu veličinu. Pri definiciji izvedenih e-ih j-a služe se obćim (racionalnim) elmg jednačbama.
a) Giorgijev sustav ima osnovne jedinice: metar, kilogram, sekunda, om. Načelno bi se veličina osnovne e-e j-e mogla uzeti po volji. Odaberemo li abs om, tad u ovaj sustav ulaze abs praktične jedinice: amper, volt, kulon, farad, henri. Uzmemo li naprotiv kao jedinicu odpora int om, tad se farad i henri u Giorgijevu sustavu podudaraju s int faradom odnosno int henrijem; no amper, volt i kulon nisu ni int ni abs, nego t. zv. semiabsolutni, jer se za njihovu definiciju služimo abs vatom (jedinica snage u Giorgijevu sustavu) i int omom. Vat je naime produkt volta i ampera, a om omjer.
Uzmemo li, da se jedinica električkog odpora Giorgijeva sustava podudara s abs omom, tad su sve jedinice novijeg elektrotehničkog sustava, nakon prielaza na abs praktične jedinice (a metar je jedinica dužine), jednake e-im j-ama Giorgijeva sustava.
b) Sustav Kalantaroffa obuhvaća poput Giorgijeva i mehaniku i elektricitetu, a po veličini se jedinice ovog sustava podudaraju s jedinicama Giorgijeva, ali se u mehanici uzimaju kao osnovne jedinice: metar, sekunda i jedinica djelovanja (predlaže se ime plank); a u elektriciteti osnovne jedinice: metar, sekunda, kulon i jedinica za magnetski naboj (predlaže se ime veber).
Jedinicu djelovanja plank treba odabrati tako, da se u tom sustavu izvedena jedinica za masu podudara s kilogramom. Tad u taj sustav idu džaul = plank/sek, zatim vat = plank/sek2. Budući da se pri definiciji e-ih j-a služimo elmg jednačbama racionalnog oblika, to se magnetski naboj i tok magnetske indukcije mjere istom jedinicom: umnožkom jedinice električkog napona i sekunde. S druge strane električki se naboj mjeri umnožkom jedinice za jakost električke struje i sekunde. Prema tome je produkt jedinica za električki odnosno magnetski naboj jednak jedinici djelovanja, jer je jedinica snage jednaka umnožku jedinica za električku struju i električki napon. U sustavu Kalantaroffa plank je umnožak dviju e-ih j-a: za električki odnosno magnetski naboj. Odaberemo li jednu od njih, tad je druga ovom određena. Ako je jedinica električkog naboja abs kulon, tad se sve e. j. podudaraju s jedinicama Giorgijeva sustava.
U sustavu Kalantaroffa vrlo je zgodna oznaka izvedenih e-ih j-a, jer je građena od met, sek, kulon, veber, budući da se svagdje u elektriciteti osnovna mehanička jedinica plank nadomješta umnožkom veber.kulon. Prema tome se u sustavu Kalantaroffa ciepa pri prielazu na područje elektriciteta osnovna mehanička jedinica plank u dvie električke.
Napomena. Vrlo je pregledna oznaka izvedenih e-ih j-a, koja se služi jedinicama amper, volt, sek, met. Tako je na pr. jedinica jakosti električkog polja volt/met. Takvo polje vlada među pločama širokog ravnog kondenzatora, kad je napon među pločama 1 volt, a razmak ploča 1 metar. Ova se oznaka može upotrebljavati jednako i u sustavu Giorgija i u sustavu Kalantaroffa.
LIT.: J. Wallot, Dimensionen, Einheiten, Maßsysteme, Handbuch der Physik II., 1926; W. Jäger, Absolute Maße und Einheiten, Handbuch der Elektrizität und Magnetismus (Graetz) II., 1921; W. Wilson, Theoretical Physics II., 1933; J. Fischer, Einführung in die klassische Elektrodynamik, 1936; G. Oberdörfer, Lehrbuch der Elektrotechnik I., 1944.V. L-ć.
Električki elementi → Članak.
Električki titraji (električke oscilacije) fizikalni su pojavi, kod kojih se periodski mienja električko stanje u vodiču i u dielektrikumu. Izraz titraj potječe iz područja mehanike. U prenesenom smislu upotrebljava se i ondje, gdje se ne radi o gibanju, već o periodskom mienjanju fizikalnih veličina, kao što su električka struja, napetost, električko i magnetsko polje.
 Sl. 1. Fotografska snimka električke iskre
Sl. 1. Fotografska snimka električke iskre
(po Feddersenu)1. Prvi pojavi električkog titranja pronađeni su kod proučavanja električke iskre. G. 1824 opazio je Savary, da se izbijanjem lajdenske boce kroz uzvojnicu može čelična igla magnetizirati »anomalno«, t. j. tako, da smjer magnetiziranja nije u skladu sa smjerom struje, koju bi dalo jednosmjerno izjednačenje električkih naboja na oblozima boce. Na temelju toga Savary je zaključio, da ne mora uviek vriediti Ampereov zakon. Ponovno je iztraživao i držeći se Franklinove teorije nastojao protumačiti ovaj pojav američki fizičar J. Henry (Washington 1842). On je uzeo, da iza prvog glavnog izbijanja lajdenske boce sliedi niz sve slabijih »refleksnih« izbijanja u izmjeničnim smjerovima. Drugom eksperimentalnom metodom odkrio je električke titraje W. Feddersen (1857). Promatrajući u zrcalu, koje se okreće, sliku iskre lajdenske boce našao je, da se ta slika sastoji od više dielova (sl. 1). Iz fotografija ove slike mogao je odrediti trajanje ili vrieme titraja. Najviše frekvencije, s kojima je Feddersen radio, iznose oko milijun u sek. Helmholtz je na temelju fizioložkih učinaka zaključio, da nastaju električki titraji, ako se polovi indukcijskog aparata nadovežu na obloge lajdenske boce (1866).
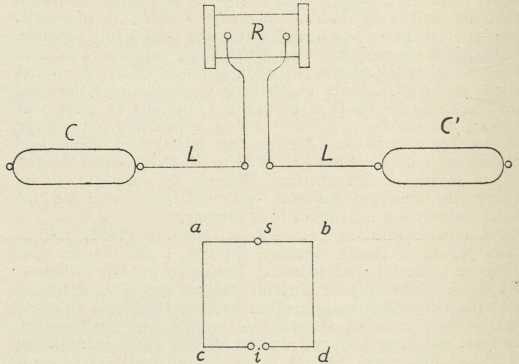 Sl. 2. Hertzov oscilator i resonator
Sl. 2. Hertzov oscilator i resonator2. U području električkih titraja osobito su važna Hertzova eksperimentalna iztraživanja (1887—89). Hertz je pokazao, da se pomoću iskre mogu proizvesti električki titraji u ravnom vodiču (dipolu), a u drugom odieljenom vodiču pobuđuju se titraji, koji su najjači u slučaju resonancije. Eksperimentalni uređaj, oscilator i resonator, nacrtan je u sl. 2. Hertzov otvoreni oscilator (»radiator«) čine 2 štapa L, L vezana na konduktore C, C', koji mogu biti kovne ploče, valjci, kugle. Kapacitet oscilatora je usredotočen u konduktorima, a samoindukcija u štapovima. Titraji se uzbuđuju Ruhmkorffovim induktorom R. Svaku iskru induktora prati nekoliko visokofrekventnih titraja. Resonator (sekundarni krug) je pravokutnik od žice određene veličine (a b c d) s iskrištem i. U slučaju resonancije, na koju utječe i veličina iskre induktora, inducira se u sekundarnom krugu tolika napetost, da se na mjestu i pojave iskre. Maksimalna dužina ovih iskara je mjera za jačinu titraja u sekundarnom krugu. Razmicanjem konduktora C, C po štapovima dobivao je Hertz različne dužine iskara i. Iz takvih pokusa izveo je krivulju resonancije s izrazitim maksimumom.
Hertz je pokazao, da su na krajevima žice a b c d trbusi, a na srednjem mjestu s čvor električne napetosti. Kod spajanja nekog mjesta žice sa zemljom umanjivala se ili je posve izčezla iskra i, dok takav spoj točke s nije nimalo na iskru utjecao. U žici Hertzova resomatora nastaju stojni električki valovi, koji se mogu razviti refleksijom titraja (periodskih električkih poremetnja) na krajevima. Klasičnim Hertzovim pokusima, kojima je Helmholtz dao poticaj, bila je svrha, da se iztraži, vriedi li za širenje električkih poremetnja starija elektrodinamska teorija, koju su razvili W. Thomson i Kirchhoff, ili novija Maxwellova. Na temelju obiju teorija moglo se očekivati, da se električki titraji šire po ravnom vodiču konačnom brzinom, koja je jednaka brzini svjetlosti. Obje su teorije uzimale, da u polju oscilatora nastaju inducirane elektromotorne sile, koje mogu izazvati električke titraje u krugu odieljenog resonatora. No dok bi prema elektrodinamskoj teoriji pojavi indukcije morali sliediti momentano, prema Maxwellovoj teoriji širila bi se indukcija kroz prostor jednakom konačnom brzinom kao električki titraj i ravnom žicom. Važno ovo pitanje rješavao je Hertz pokusom, koji je H. Poincaré nazvao pokus razkršća (experimentum crucis). Uzporedno s pločom Hertzova oscilatora (sl. 2) stoji druga ploča, na kojoj je učvršćena 60 m duga žica s izoliranim slobodnim krajem. Pomicanjem udešenog resonatora duž ove žice određivao je Hertz mjesta najkraće i najduže iskre, t. j. čvorove i trbuhe stojnih električkih valova, koji su se na žici razvili. Našao je, da na valnu dužinu ne utječe tvar vodiča. Bakrena i željezna žica davale su jednako duge valove kao ciev napunjena razrieđenom sumpornom kiselinom. Pomoću formula za kapacitet i samoindukciju izračunano je za Hertzov oscilator vrieme titraja T = 2∙10-8 sek, dok je mjerenje davalo λ/2 = 2,8 m. Za brzinu širenja električkih valova u žici izlazi c= λ/T 280 000 km/sek. Radi jedne pogrješke u izračunavanju kapaciteta izašla je Hertzu vriednost c = 200 000 km/sek, i on je neslaganje s teoretskom vriednosti (c = 300 000 km/sek) pripisivao nepoznatom uzroku. Na pogrješku Hertzova računa upozorio je H. Poincaré (1891). Kasnija mjerenja Lechera (1890), Blondlota (1891), Drudea (1902) i dr., izvedena s kraćim električkim valovima, pokazala su sklad s teorijom.
U drugom nizu pokusa iztraživao je Hertz, kako na resonatorski krug utječu progresivni prostorni električki valovi zajedno s progresivnim valovima na žici, koji se mogu razviti, ako je slobodan kraj žice odveden u zemlju. Ako bi se oba valna niza širila različnim brzinama, mienjala bi se fazna razlika, s kojom oni interferiraju, periodski, a to bi se opažalo kod udaljivanja resonatora. U slučaju, da su brzine širenja jednake, valni bi nizovi, radi stalne fazne razlike, u svim daljinama na isti način interferirali. Radi mnogih smetnja i potežkoća, koje su nastajale zbog dugih valova (λ = 5 do 6 m) i nedovoljno velike prostorije eksperimentiranja, nisu Hertzovi eksperimenti ove vrste davali jasne rezultate. Naknadni Hertzovi pokusi sa stojnim električkim valovima (1893) slagali su se sa zahtjevima Maxwellove teorije.
Služeći se kraćim električkim valovima (λ ~ 60 cm) izveo je Hertz niz pokusa, kakvi se izvode s valovima svjetlosti i zvuka. Kao oscilator za kratke valove upotrebljavao je Hertz 26 cm dugi, 3 cm široki mjedeni štap s iskrištem u sredini, namješten u žarištnoj crti paraboličnog zrcala. Pomoću linearnog resonatora mogao je sliediti tečaj valova kroz daljinu 16 m. S tim valovima, koje je Hertz zvao zrakama električke sile, izvodio je on eksperimente o refleksiji na kovnom zrcalu, o lomu u prizmi od izolatora, o ogibu, interferenciji i polarizaciji. Znamenit Hertzov rad na području električkih titraja nastavili su brojni iztraživači, eksperimentatori i teoretičari, među kojima se iztiču imena Lodge, Righi, Poincaré, M. Abraham, J. J. Thomson, M. Wien, Marconi.
 Sl. 3. Uređaj za visoku frekvenciju
Sl. 3. Uređaj za visoku frekvenciju
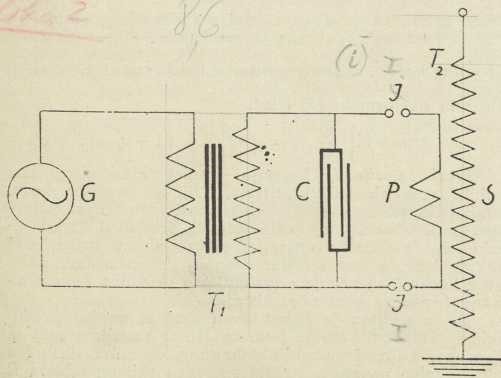
(po Tesli)3. Teslini titraji. Poslije Hertzovih pokusa izvodio je Tesla poznate eksperimente s visokofrekventnim titrajima (»Tesline struje« visoke napetosti i visoke frekvencije, 1890—93). Jedan Teslin uređaj pokazuje sl. 3, u kojoj je sa G označen generator jednofazne struje, T1 transformator za nizku frekvenciju, C kondenzator (Teslin oblik), I—I iskrišta, T2 Teslin transformator. Transformacijom uvećana napetost generatora dolazi na obloge kondenzatora, koji se izbija kroz iskrišta i primarni svitak P Teslina transformatora. U sekundarnoj uzvojnici S s vrlo mnogo zavoja, koje vlastiti titraji moraju biti u resonanciji s titrajima primarnog kruga, nastaju indukcijom visokofrekventni titraji velike napetosti. Primarni krug s iskrištem vrši ulogu transformatora za visoku frekvenciju. Pomoću Teslina transformatora bez željezne jezgre, s uljem u svrhu izolacije, postizava se metodom resonancije mnogo puta veća napetost, nego što bi je dao obični transformator. Tesla je izgradio vrlo snažne aparature s turbinama prekidačima, koje su kod frekvencije od više stotina hiljada u sek. davale napetost od nekoliko milijuna volta i više metara duge iskre (sl. 4). Teslin su transformator upotrebljavali u početnim sustavima radiotelegrafije (Braun, Marconi od 1898 dalje). Marconi se služio Teslinom aparaturom, kad mu je uspjela prva prekooceanska brzojavna veza između Evrope i Amerike (1901). Tesla se služio i složenim iskrištem te postigao »gašene titraje« s malenim prigušenjem. Radi neznatnih elektrolitičkih učinaka visoka napetost Teslinih titraja nije opasna za ljudsko tielo. Malene Tesline aparature služe u svrhe diatermije i električke masaže. Teoriju Teslina transformatora obradio je Drude (1903). Školske Tesline aparature konstruirali su Himstedt, Grimsehl, Elster i Geitel. U svrhe atomske fizike upotrebili su Teslin transformator američki iztraživači Lawrence, Sloane, Tuve i dr. (1930).
 Sl. 4. Izbijanje Teslina transformatora
Sl. 4. Izbijanje Teslina transformatora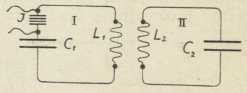 Sl. 5. Induktivno vezani krugovi titranja
Sl. 5. Induktivno vezani krugovi titranja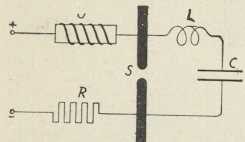 Sl. 6. Lučni plamen kao generator
Sl. 6. Lučni plamen kao generator
elektr. titraja (po Duddellu)4. Metoda gašenih iskara (uzbuđenje udarima). Jaki električki titraji mogu se uzbuditi u zatvorenom krugu II (sl. 5) tako, da se on induktivno veže s krugom oscilatora I, koji je uzbuđen iskrama. Ako krugovi I i II imaju približno jednake frekvencije, nastaje »pojava udara«. U jednoj vremenskoj periodi prelazi električka energija iz kruga I u II, a u sliedećoj se vraća u krug I. Takav se proces mnogo puta ponavlja. Ovdje postoje slične prilike kao kod dva njihala, koja su vezana elastičnom spiralom (Oberbeckov pokus). U krugu II uzbuđena energija može se vratiti u primarni krug, ako se u zgodnom času iskra naglo uguši, t. j. ako je krug I prekinut. Uvjete za brzo gašenje iskre izpunjava Wienovo složeno iskrište sastavljeno od većeg broja uzporednih, posrebrenih bakrenih ploča u malenim razmacima. Iskre se brzo gase radi naglog prestanka ionizacije. Gusti niz kratkih iskara daje visoki ton (tönende Löschfunken, spark quenched, étincelles étoufées). Prije uvođenja elektronske cievi sustav je gašenih iskara vrlo dobro služio u svrhe radiotelegrafije na velike daljine (M. Wien, 1906/7).
5. Neprigušeni titraji lučnog plamena. W. Duddell je pokazao, da se neprigušeni električki titraji mogu načiniti pomoću lučnog električkog plamena (1900). Na sl. 6 je nacrtan Duddellov spoj. Preko odpornika R i ugušivača U spojeni su polovi lučne lampe s izvorom stalne napetosti (200 volta). S druge su strane na lučni plamen S priključeni samoinduktivni svitak L i kondenzator C. Uz povoljne uvjete uzbude se u krugu (LCS) neprigušeni titraji s periodom T=2π√LC. Zvučne se frekvencije ovdje lakše postizavaju nego visoke. Radi promjenljive struje lučnog plamena ugrijava se čas jače, čas slabije okolni uzduh. Time nastaju zvučni titraji, koje uho zamjećuje kao ton (zviždeći lučni plamen).
 Sl. 7. Generator s lučnim plamenom
Sl. 7. Generator s lučnim plamenom
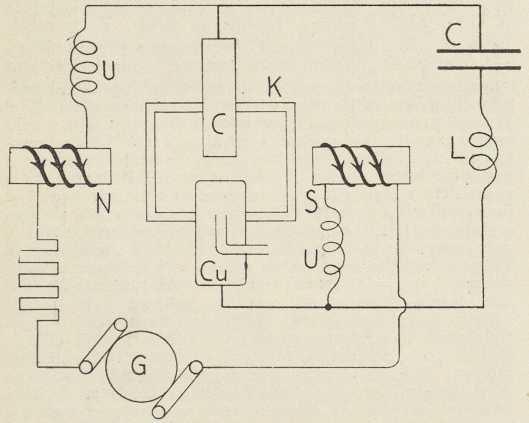
(po Poulsenu)Duddellovu metodu usavršio je W. Poulsen (1903). Sl. 7 pokazuje shemu Poulsenove lučne lampe s krugom titranja (LC). Anoda je bakren valjak, hlađen vodom, a katoda homogeni ugljen. Obje se elektrode okreću. Jednoliko gorenje plamena postizava se kapanjem žeste u komoricu K. Time se stvara atmosfera vodika. Magnetsko polje među polovima N, S ima svrhu, da iz plamena iztjera ione. Ugušivači U U prieče prielaz titraja u generator G. Poulsenove generatore za duge električke valove (do 24.000 m) upotrebljavale su velike svjetske radio-postaje do novijeg vremena.
6. Elektronska ciev kao generator električkih titraja → elektronska ciev.
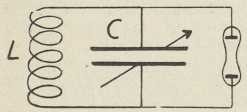 Sl. 8. Shema mjerača frekvencije
Sl. 8. Shema mjerača frekvencije
s Geisslerovom cievi7. Za mjerenje frekvencije krugova titranja služi na resonanciji osnovan mjerač frekvencije (Dönitz, 1903). Glavni dielovi aparata jesu kondenzator »na vrtnju« i nekoliko uzvojnica za različna područja frekvencije. Kondenzator i uzvojnica čine zatvoren krug titranja (sl. 8), koji se induktivno veže s krugom, kojega frekvenciju određujemo. Kapacitet kondenzatora se mienja, dok ne nastupi resonancija, koju pokazuje na kondenzator priključena Geisslerova cjevčica ili telefonska slušalica s kristalnim detektorom (ili s tickerom) ili osjetljivi vatmetar s tankom žicom. Ako je skala kondenzatora baždarena u valnim dužinama, aparat se zove valomjer (Wellenmesser, ondomètre, wavemeter).
Postoji nekoliko metoda za baždarenje mjerača frekvencije. Kod jedne metode izračunavaju se pojedine frekvencije iz poznatih vriednosti samoindukcije (L) i kapaciteta (C). Ove vriednosti se dobivaju iz formula za L i C, u kojima dolaze dimenzije kondenzatora i samoinduktivnog svitka. Za vrlo točno baždarenje služi piezoelektrički kvare.
8. Teorija električkih titraja. Prije spomenutih Feddersenovih pokusa došao je W. Thomson teoretskim iztraživanjima do spoznaje, da je izbijanje kondenzatora oscilatoran pojav. U Thomsonovu krugu titranja, koji je sastavljen od kondenzatora s kapacitetom C i stalne samoindukcije L, označit ćemo s q momentani naboj, s V momentanu napetost kondenzatora, s i momentanu struju, s r odpor samoinduktivnog svitka. Da je krug bez odpora, ostao bi zbroj elektrostatske energije (1/2q2/C) i magnetske energije (1/2 Li2) stalan (zakon energije). Radi odpora r prelazi u vremenu dt dio ciele energije u Jouleovu toplinu i2 r dt. Iz
-d(1/2q2/C + 1/2Li2) = i2rdt
izvodi Thomson diferencialnu jednačbu električkog titraja
\(\qquad\qquad\displaystyle \cfrac{\rm d\;q}{\rm dt^2}+\cfrac{\rm r}{\rm L}\cfrac{\rm d\,q}{\rm d\,t}+\cfrac1{\rm LC}=0\qquad\qquad\)(1)
i dolazi do rješenja
q = K1.e + K2 e , gdje je α1, α2 = r/2L ± √r/4L2-1/LC.
U sličnim jednačbama mjesto q dolazi V odnosno i.
Ako je izraz pod znakom koriena 0, izlaze za α1, α2 realne vriednosti. U tom je slučaju izbijanje kondenzatora aperiodsko (bez titraja). Ako je r’/4L2 < 1/LC, rješenje se svodi na oblik q = Q e-kt sin (ωt + φ), u kojem je (2)
\(\qquad\qquad\displaystyle {\rm k}=\cfrac{\rm r}{\rm 2\;L},\quad\omega=\sqrt{\cfrac1{\rm L\;C}-\cfrac{\rm r^2}{\rm 4\;L^2}},\quad\varphi=\text{faza titraja.}\)
Slične formule vriede za napetost i struju. Između struje i napetosti postoji razlika faze π/2.
Označimo li sa τ vrieme titraja, radi relacije ωτ=2π, sliedi
\(\qquad\displaystyle \boxed{\tau=\cfrac{2\;\pi^2}{\sqrt{\cfrac1{\rm L\;C}-\cfrac{\rm r^2}{\rm 4\;L^2}}}}\quad{\text{(Thomsonova formula za }\atop\text{prigušene sinus-titraje, 1853).}}\qquad\qquad\)(3)
Smije li se r2 zanemariti prema 4L/C, izlazi
\(\;\displaystyle\boxed{\tau=2\;\pi\;\sqrt{\rm L\;C}}\)
. U Thomsonovoj teoriji nije uzet u račun gubitak energije emisijom električkih valova u prostor.
Iz formule (2) sliedi, da je omjer amplituda istog smjera za dvie susjedne periode jednak
\(\qquad\qquad\displaystyle\cfrac{\rm Q}{\rm Q'}={\rm e}^{\tiny\cfrac{\rm 2\pi k}{\omega}}={\rm e}^{\small\rm k\tau}.\)
Kao mjera za prigušenje titraja (Dämpfung, ammortissement, damping) odabrana je veličina
ϑ = log nat Q/Q′ kτ (logaritamski dekrement titraja).
Obzirom na formulu (3) izlazi
\(\qquad\qquad\displaystyle\vartheta=\pi\;{\rm r}\;\sqrt{\cfrac{\rm C}{\rm L}},\quad\tau=2\;\pi\;\sqrt{{\rm L\;C}\;\left(1+\cfrac{\vartheta^4}{4\;\pi}\right)}\;.\)
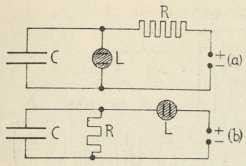 Sl. 9. Spojevi za dobivanje slobodnih
Sl. 9. Spojevi za dobivanje slobodnih
preskočnih titraja (po Schröteru)9. Preskočni titraji. U novijoj tehnici važnu ulogu ima osobita vrst električkih titraja, koji se zovu preskočni titraji (Kippschwingungen, Relaxationsschwingungen, kippvibration). Obćenito se može reći, da preskočni titraji nastaju, ako električka energija, preko labilne točke, preskakuje između dva stabilna stanja. Prema načinu dobivanja i tehničkoj primjeni razlikujemo slobodne i sinhronizirane (prisilne) preskočne titraje.
U sl. 9a nacrtan je jednostavan spoj za dobivanje slobodnih preskočnih titraja pomoću lampe tinjalice (spoj sa bljescima, Glimmlampenblinkschaltung, Schröter, 1919). Na polove stalne napetosti stavlja se preko velikog odpora R kondenzator C (na pr. 1μf) i s njim uzporedno lampa-tinjalica L. Ova lampa ima svojstvo, da kod točno određene napetosti paljenja Vp počne svietliti, a utrnjuje kod nešto niže napetosti gašenja Vg. Razlika Vp—Vg iznosi nekoliko volta. Kad lampa-tinjalica svietli, ima malen odpor, a kad je utrnuta, odpor je neizmjerno velik. U času, kada radi uvrštenog odpora R na oblozima kondenzatora naraste napetost do vriednosti Vp, kondenzator počne izbijati kroz maleni nutarnji odpor tinjalice. Ovo izbijanje traje, dok se napetost snizi do vriednosti Vg. U tom času lampa-tinjalica utrne, a kondenzator se ponovno nabija do napetosti Vp.
Na osnovi sheme u sl. 9a dobivao je preskočne titraje već Hittorf (1859). Služio se kod toga Geisslerovom cievi.
Sl. 9b pokazuje nešto izmienjeni spoj. Vremena nabijanja i izbijanja kondenzatora za spoj 9a jednaka su vremenima izbijanja i nabijanja za spoj 9b. Perioda preskočnog titraja ista je za oba slučaja.
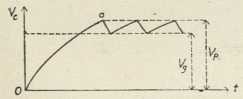 Sl. 10. Zavisnost napetosti preskočenih
Sl. 10. Zavisnost napetosti preskočenih
titraja o vremenuU sl. 10 promjene napetosti grafički su prikazane. U točki a počinje pravilan pojav preskočnih titraja. Radi zubčastog oblika krivulje V = f(t) dobili su ovakvi titraji ime zubčasti titraji (Sägezahnschwingungen). Početnom dielu Oa krivulje napetosti pripada jednačba
Vc = V(1-e-1/RC),
u kojoj je V zadana stalna napetost, Vc napetost kondenzatora, 1/RC vremenska konstanta. Za frekvenciju preskočnih titraja (Kippfrequenz, preskočna frekvencija) vriedi približno formula
\(\qquad\qquad\displaystyle {\rm f}=\cfrac1{{\rm RC\;log\;nat}\cfrac{\rm V-V_g}{\rm V-V_p}}.\)
Recipročna vriednost 1/f = t nazvana je preskočnom periodom.
Od tehničkih primjena slobodnih preskočnih titraja spominjemo napravu za bljeskanje (Blinkgerät), zujalo s lampom tinjalicom i glasbeni instrument trautonij (→ elektroakustika 4).
Pomoću izmjenične napetosti mogu se procesom interferencije preskočni titraji sinhronizirati. To se postizava time, da se za R i C odaberu vriednosti, za koje je preskočna frekvencija bliza frekvenciji napetosti, koja se izpituje.
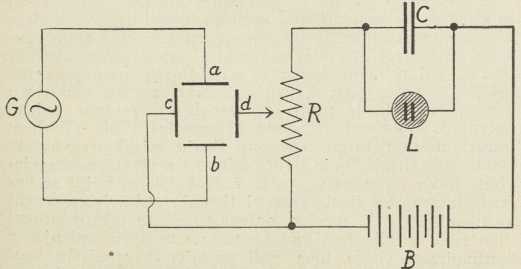 Sl. 11. Shema za preskočni uređaj
Sl. 11. Shema za preskočni uređaj
katodnog oscilografaPojav sinhroniziranih preskočnih titraja primjenjuje se kod katodnog oscilografa. Na sl. 11 nacrtan je jednostavan uređaj (preskočna sprava, Kippgerät) za tu svrhu, (a, b) i (c, d) parovi su uzporednih ploča, koji odklanjaju katodnu zraku. Polovi izmjenične napetosti G, koja se oscilografski izpituje, vezani su na pločice a, b. Pločice c, d drugog para u vezi su preko potenciometra R s baterijom B i s krugom preskočnih titraja, koji je sastavljen od lampe tinjalice L i kondenzatora C. Ovdje se izkorišćuje pojav, da se za vrieme nabijanja kondenzatora napetost VR = V—VC na krajevima odpornika R jednoliko umanjuje, a kad lampa tinjalica zasvietli, VR naraste. Radi toga su pomaci oscilografske mrlje u horizontalnom smjeru (vremenska abscisa) proporcionalni s vremenom. U obzir dolazi samo početni pravčasti dio eksponencialne krivulje za napetost VR. Preskočna perioda t udešava se prema periodi napetosti G tako, da oscilografska slika miruje.
Postoje mehanički pojavi, koji se mogu uzeti kao analogija za preskočne električke titraje. Takvi su pojavi periodski udarci vode u cievi hidrauličkog ovna, zujanje žica brzojavnog voda djelovanjem vjetra, sviranje vodovoda. Prema van der Polu i van der Marku svode se na mehaničke preskočne titraje neki bioložki procesi, koji vode do srdčane kapi.
LIT.: Hertz, Gesammelte Werke II., 1892; W. Thomson, Mathematical a. phys. papers I., 1882; Richter, Elektr. Kippschwingungen, 1940.D. P-ć.
Električki valovi → Elektromagnetski valovi.
Elektroakustika je novija grana primienjene (tehničke) akustike. Razvila se u posljednje vrieme u vezi s tehnikom visoke frekvencije. U širem smislu rieči obuhvaća e. sva iztraživanja o zvučnim titrajima izvedena električkim pomagalima.
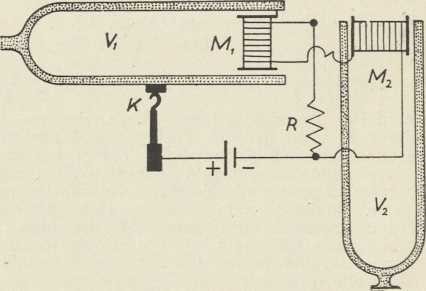 Sl. 1. Viljuške za jake tonove
Sl. 1. Viljuške za jake tonove
(po Dvořáku)1. Najstarije elektroakustičke sprave jesu viljuške, žice, membrane s električkim pogonom. Na sl. 1 nacrtan je aparat za jake tonove s 2 elektromagnetske viljuške (Dvořák, 1884). Titraji obiju viljušaka (V1, V2), koje su udešene na isti ton, uzbuđuju se i uzdržavaju pomoću dva elektromagneta M1, M2, kroz koja teče ista struja magnetiziranja izprekidana kontaktom K. Pomoću velikog odpora R, koji trajno spaja uzvojnice obaju elektromagneta, ugušuje se iskra, kad je struja prekinuta. Radi resonancije između impulsa struje magnetiziranja i titraja viljuške V2, daje ova viljuška, koja počiva na kutiji-resonatoru, glasan ton. U novije vrieme upotrebili su za pogon elektromagnetske viljuške generator s elektronskom cievi. Takva viljuška od čelika invara, smještena u termostat, daje ton s konstantnošću 10-7 do 10-8 pa može služiti kao normala zvučne frekvencije (D. W. Dye, 1923).
Najrazširenije elektroakustičke sprave jesu elektromagnetski telefon (Bell, 1874) i mikrofon s promjenljivim odporom (Hughes, 1878). Na njihovu usavršenju radili su stručnjaci kroz decenije. Edison u USA i Siemens u Njemačkoj načinili su prve telefone za glasni govor, koji odgovaraju današnjim elektromagnetskim zvučnicima. U Parizu su 1881 priredili prienos glasbe žicom za 20 slušača. Služeći se telefonima za glasni govor Edison je 1891 u New-Yorku priredio pokus, kod kojeg je oko 1000 ljudi slušalo prienos iz gradske opere. Pomoću većeg broja telefona postizavala se plastična reprodukcija. Ovakvi se pokusi mogu smatrati predtečama današnje radiofonije. Elektroakustička iztraživanja toga vremena ubrajali su u tehniku slabe struje.
2. S izumom elektronske cievi počeo je novi razvoj e-e. Ova je ciev služila najprije kao zvučno pojačalo kod običnog telefonskog saobraćaja. Najveća je njezina vriednost, što u oscilatorskim spojevima proizvodi visokofrekventne električke titraje i valove, koji služe kao nosioci zvučnih titraja i omogućuju prienos govora i glasbe radiofonijom. Starije konstrukcije telefona i mikrofona nisu zadovoljavale zahtjevima radiofonije. Da se postigne vjerna reprodukcija zvuka, trebalo je starije sprave preudešavati i nove konstruirati.
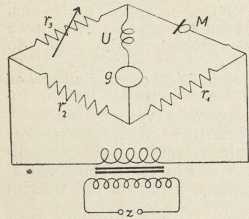 Sl. 2. Shema za automatsku
Sl. 2. Shema za automatsku
analizu zvuka (po E. Meyeru)3. Analiza zvuka. Između mnogih zadaća, koje novija e. obrađuje iztiče se analiza zvuka. Ovdje se određuje amplituda i frekvencija komponenata (parcialnih tonova), od kojih se sastoji neki složeni ton (zvek) ili zamršeniji zvučni titraj. Za subjektivnu analizu zvuka upotrebljavali su najprije Helmholtzove resonatore. Sliedila je Fourierova analiza, koja iz oscilograma (krivulje titraja) nakon dugog računanja daje frekvencije i amplitude parcialnih tonova. Velik napredak u ovom području postignut je automatskim električkim metodama. U sl. 2 skicirana je najjednostavnija takva metoda po E. Meyeru (1928). U jednoj grani spoja za Wheatstoneov most nalazi se mikrofon sa zrncima od ugljena (M), a u ostalim granama odpori r1, r2, r3. Kroz grane mosta prolazi transformirana izmjenična struja I sin 2πft iz zujala z (→ batić-prekidač). Zujalo daje ton, kojemu se frekvencija f može mienjati. Odpori r1, r2, r3 tako su odabrani, da u mostu nema struje. Radi jednostavnosti uzet ćemo sada, da na mikrofon dolaze zvučni valovi jedne frekvencije p, koju pomoću skupine frekvencija f treba odrediti. U mikrofonu interferiraju obje frekvencije p, f. Označit ćemo sa I amplitudu struje, koja teče mikrofonom, sa R stalni dio njegova odpora, sa ∆R sin 2πpt promjenljivi dio. Za napetost, pod kojom se nalazi mikrofon, vriedi formula
V = (R + ∆R sin 2πpt) I sin 2πft.
Ovaj se izraz može svesti na oblik
V = IRsin2πft + I∆R/2cos(p — f)t — I∆R/2cos(p + f)t,
u kojem dolazi frekvencija tona diferencije (p—f) i frekvencija tona sume (p+f). Postupak kod analize je ovaj. Puštamo, da mikrofonom teku redom izmjenične struje ciele skupine frekvencija f. U most uvršten instrument g, udešen za uzko područje nizkih frekvencija, može mjeriti samo amplitudu vrlo dubokog tona diferencije f—p. Ova je amplituda razmjerna sa ∆R, a približno i s amplitudom tona p, tako da g mjeri amplitudu toga tona. Dolaze li na mikrofon valovi složenog tona, određuju se na jednaki način, prelazeći cielu skupinu frekvencija zujala, amplitude i frekvencije pojedinih parcialnih tonova. Kao mjerači instrument g služi na torziji osnovan galvanometar s niti, u seriji s ugušivačem U. Ova se metoda ne može upotrebiti za analizu glasova i šumova, gdje dolazi množtvo blizih parcialnih tonova.
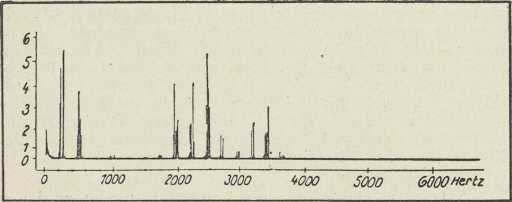 Sl. 3. Zvučni spektar vokala «I»
Sl. 3. Zvučni spektar vokala «I»Za analizu vokala upotrebljava se automatska metoda po M. Grützmacheru. I ovdje dolazi do interferencije sastavnih komponenata složenog tona, koji analiziramo, i kontinuiranog skupa frekvencija f (od 16 do 10 000 u sek). U aparaturu ugrađen električki filtar (Tiefpassfilter) propušta u napravu za registriranje samo vrlo duboke tonove diferencije (na pr. f = 20/sek). Sl. 3 pokazuje zvučni spektar pjevanog vokala »i«. Na horizontalnu os nanesene su frekvencije, a vertikalni potezi znače jakosti parcialnih tonova. Dvie odieljene skupine parcialnih tonova, u okolini f = 300 i f = 2500 pripadaju sporednom i glavnom formantu vokala »i«.
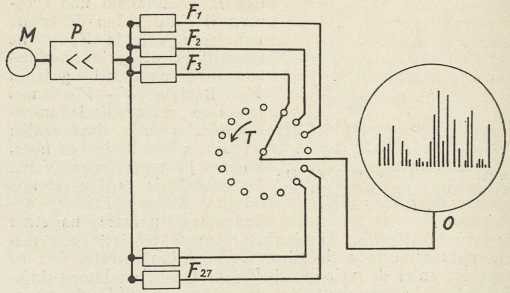 Sl. 4. Shema zvučnog spektrometra
Sl. 4. Shema zvučnog spektrometraNajnoviji aparat za analizu zvuka, nazvan »zvučni spektrometar« (Freystedt, 1935; tt Siemens), prikazan je shematski u sl. 4. Dielovi aparata jesu: mikrofon M, pojačalo P, 27 električkih filtara F, kontakti sa zajedničkom tipkom T, katodni oscilograf O. Svaki pojedini filtar propušta trećinu oktave. Propustljivost sviju filtara zajedno obuhvaća frekvencije od 36 do 18 000 u sek. Tipka T, koja 20 puta u sekundi prelazi preko kontakata, spaja redom pojedine filtre s oscilografskom cievi. U svakom je času vertikalni odklon svietle mrljice oscilografa razmjeran s jakosti one komponente, koju filtar propušta. Mirne slike se dobivaju sinhronizacijom okretanja tipke i horizontalnog odklanjanja mrljice. Na sl. 5 vidimo ovakvu aparaturu, koja služi i za analizu štropota i šumova. Sl. 6a pokazuje Siemensovim aparatom snimljen spektar štropota stroja za pisanje, a sl. 6b spektar aeroplanske buke (→ buka). Na toj se slici vidi, kako je grupa nizkih frekvencija, koje pripadaju motoru, odieljena od viših frekvencija, koje potječu od zračnog vijka.
 Sl. 5. Zvučni spektrometar
Sl. 5. Zvučni spektrometar
TT. Siemens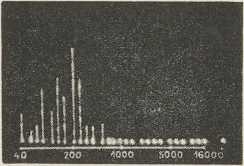 Sl. 6a. Spekar štropota
Sl. 6a. Spekar štropota
stroja za pisanje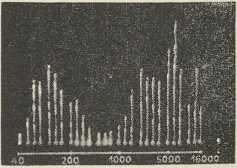 Sl. 6b. Spektar buke
Sl. 6b. Spektar buke
što je izvidu aeroplan4. Električka glasba. U posljednja 2 decenija sagrađeni su glasbeni instrumenti, kod kojih se tonovi proizvode električkom aparaturom. U takvim električkim glasbalima možemo razlikovati 4 sastavna diela: 1. generator električkih titraja, kojim ravna igrač; 2. pojačalo; 3. uređaj za namještenje boje tona; 4. zvučnik. Najpoznatije električko glasbalo načinio je ruski tehničar L. S. Teremin (njem. patent S. Goldberg u. Söhne [Theremin] 1924). Glasbeni tonovi nastaju interferencijom dvaju visokofrekventnih električkih titraja, koje daju oscilatori s elektronskim cievima. Kako je naznačeno u sl. 7, iz kutije, u kojoj se nalaze elektronske cievi, krugovi titranja i dr., izlazi kovni vertikani štap A, nazvan antena. Kad se takvoj anteni dlan ruke približuje i kad se od nje udaljuje, mienja se kontinuirano visina tona radi promjene kapaciteta krugova titranja. Micanjem ruke kroz daljinu 1 m dobivaju se 3 oktave tonova, što je dovoljno za izvedbu jednostavnijega glasbenog komada. Jakost tona se udešava pomoću odpornika, koji se nalazi u krugu zvučnika na ulazu u pojačalo. Takav odpornik sastoji se od 2 kovne ploče, među kojima se nalazi prah od ugljena. Preko pedala pritište igrač jednom nogom na takav odpornik (v. sl. 8). Nagle prielaze tonova izvodi igrač tako, da lievom rukom pritisne na tipku i tim na kratak čas prekida vezu sa zvučnikom. Radi toga, što igrač traži tonove rukom u prostoru (»eteru«), nazvana je ovakva sprava glasbalo s valovima etera. Ovakav aparat načinjen je i kao dodatak radioaparatu. Tehnika igre s Tereminovim aparatom bez tipaka dosta je težka.
 Sl. 7. Shema za električko glasbalo
Sl. 7. Shema za električko glasbalo
od teremina Sl. 8. Igrač s tereminovim glasbalom
Sl. 8. Igrač s tereminovim glasbalomDrugi, dosta popularan glasbeni instrument, trautonij, konstruirao je F. Trautwein (1930). Glasbene tonove daju električki preskočni titraji (→ električki titraji 9), koji se izvode pomoću lampe tinjalice ili pomoću ionske cievi s užarenom katodom (vrsta tiratron – cievi). Aparat radi s nizom tipaka. Više ovakvih sprava načinili su Amerikanci, no praktički uspjeh se postigao samo s nekoliko električkih glasbala.
Iza klasičnih radova Rayleigha i Helmhotza nastao je zastoj u obrađivanju problema obće akustike. Naglim razvojem elektroakustike prošireno je naše znanje u svim područjima nauke o zvuku.
LIT.: A. H. Davis, Modern Acoustics, London 1934; F. Trendelenburg, Fortschritte d. physikalischen u. technischen Akustik, 2. izd., 1934; P. Lertes, Elektrische Musik, 1933; Revue d’Acoustique (osn. 1931); Akustische Zeitschrift (osn. 1936).D. P-ć.
Elektroanaliza je postupak kvantitativnog određivanja kovina s pomoću elektrolize (v.) tokom kemijske analize. Kovina se izluči iz svoje otopine s pomoću električke struje na izvagnutoj negativnoj elektrodi te nakon pranja i sušenja odredi ponovnim vaganjem elektrode. Kao negativna elektroda (katoda) obično služi platinska elektroda u obliku mreže, ili platinska zdjelica, ili elektroda od žive. Pozitivna je elektroda (anoda) u obliku spiralne platinske žice. Elektroliza se vrši u aparatu za elektrolizu. Elektrolizom kod povišene temperature i miešanjem kao i uz upotrebu veće jakosti struje pospješuje se izlučivanje kovina: brza elektroliza. Kako se svaka kovina izlučuje kod izvjestne, za nju karakteristične napetosti (napetost raztvaranja → elektrokemija), to je moguće s pomoću elektroanalize jedne otopine od više kovina odrediti svaku posebno. E-om određuje se obično bakar, nikal, kobalt, cink, srebro, živa, bizmut, antimon, kositar te kalij i natrij (na živinoj elektrodi). Na anodi se izlučuju i određuju u obliku peroksida olovo i mangan.
LIT.: Classen-Daneel, Quantitative Analise durch Elektrolyse, 7. izd., Berlin 1927; Berl-Lunge, Chemisch-technische Untersuchungsmethoden, sv. II/2., 8. izd., Berlin 1932.I. F-ć.
Elektrode. Ploče ili štapići od kovine ili ugljena, koji služe za dovod električke struje u tekući elektrolit ili u stupac plina, zovu se elektrode (= putovi elektriciteta). Elektroda, kroz koju (pozitivna) struja ulazi, zove se anoda. Druga elektroda, koja se priključuje na negativni pol napetosti, zove se katoda (Faradayeva terminologija). I ploče galvanskog članka nazvane su elektrodama.
Elektrode vakuum-cievi načinjene su velikim dielom od aluminija, jer se ova kovina električkim izbijanjem najmanje razpršuje. U nutrašnjosti cievi na svaku od ovih elektroda nadovezan je komadić žice od platine ili molibdena, koji je u staklo utaljen i vodi do vanjske kovne kapice, na koju se priključuje napetost. Uzimaju se ove kovine, jer imaju jednak koeficient raztezanja kao staklo. Načinjene su i vakuum-cievi (Geisslerove cievi) s elektrodnim oblozima na vanjskim stranama staklene stiene.
Material elektroda utječe na pad katodne napetosti. Radi toga izrađuju se elektrode neonske lampe-tinjalice od željeza. Neke aparature imaju različne uređaje za hlađenje elektroda (Röntgenove cievi, lampe sa živinim parama i dr.). Prema broju i vrsti elektroda dobile su elektronske cievi s užarenom katodom imena: dioda, duodioda, trioda, tetroda, binoda, pentoda, heksoda, oktoda.D. P-ć.
Elektrodinamika je dio nauke o elektricitetu. Obrađuje ponderomotoričke pojave izazvane djelovanjem magnetskog toka na električku struju ili djelovanjem električke struje na feromagnetičko sredstvo ili djelovanjem dviju struja jedne na drugu. Područje joj nije oštro omeđeno; kod nekih pisaca ona obuhvaća i elektromagnetizam i inducirane struje sa svim pojavima, koji se na to nadovezuju. Ampère (1822) je elektrodinamskim pojavima nazvao djelovanje struje na struju. Ovo prvobitno ograničenje sačuvalo se danas djelomično u nomenklaturi sprava za mjerenje, jer se u elektrodinamske sprave u užem smislu ubrajaju one, koje se temelje na uzajamnom djelovanju struja.
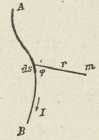 Sl. 1.
Sl. 1.1. Djelovanje struje na t. zv. magnetski pol. Biot i Savart su 1820 odmah poslije Oerstedova odkrića magnetnog polja električne struje eksperimentalno našli izraz za silu F, kojom struja jakosti i u bezkonačno dugoj ravnoj žici djeluje na magnetski pol jakosti m u daljini r. Ta je sila: F = C 2im/r, gdje je C konstanta proporcionalnosti, kojoj vriednost zavisi o sustavu jedinica. Laplace je na temelju toga izračunao silu f, kojom na magnetski pol djeluje elemenat struje, okomit na spojnicu r magnetskog pola sa sredinom elementa, a Biot je Laplaceov izraz posveobćio za bilo koji elemenat struje. Ta Biot-Laplaceova formula glasi: f = C∙im∙ds/r’∙sinφ, r gdje je φ kut, koji spojnica iz sredine elementa ds do magnetskog pola m zatvara s elementom ds (sl. 1). U literaturi nazivaju običnije ovu formulu Biot-Savartovim (elementarnim) zakonom. Sila f je okomita na ravnini položenoj kroz ds i r, a njezin smjer izlazi iz Ampèreova pravila plivača (v.). Analogno vriedi i za silu F; ona izlazi integracijom iz elementarne formule. Za m = 1 dobivamo jakost magnetskog polja H u daljini r. Za stalno r je H stalno; prema tome su magnetske silnice pravčaste struje koncentrični krugovi (→ elektromagnetizam).
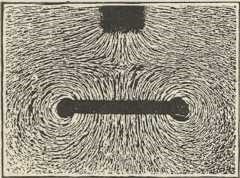 Sl. 2. Međusobno odbijanje magnetskog
Sl. 2. Međusobno odbijanje magnetskog
pola i istoimene strane magnetskog lista
prikazano silnicamaIsto tako se integracijom dobiva iz elementarnog zakona jakost polja u jednoj točki na osi kruga kružne struje. Ako je r polumjer kruga, a sve se veličine izraze u jedinicama elektromagnetskog cgs sustava, onda je jakost magnetskog polja u točki, koja leži na osi u daljini a od središta:
\(\;\displaystyle H=2\pi i\cdot\cfrac{r^2}{(r+a^2)^3}\;\)
ersteda, a jakost polja u samom središtu kruga je
\(\;\displaystyle H=\cfrac{2\pi i}r\;\)
ersteda. Odatle se, pomoću kruga s polumjerom 1 cm, definira elektromagnetska cgs-jedinica jakosti struje (= 10 ampera) kao jakost struje, koja u središtu tog kruga proizvodi magnetsko polje jakosti 2π ersteda. Pravac polja je os kruga, a njegov smjer dan je ovim pravilom: ako za gledaoca struja teče u krugu smjerom kazala na uri, na strani, okrenutoj gledaocu, magnetske silnice ulaze u krug. Prema tome krug struje vlada se kao bezkonačno kratak magnet; to je t. zv. magnetski list. To se dokazuje Ampèreovim pokusom (1820) o vladanju magnetskog lista u zemaljskom magnetskom polju (→ Ampèreov stalak). Odbijanje između magnetskog lista i istoimenog magnetskog pola prikazano je u slici 2 pomoću magnetskih silnica.
 Sl. 3.
Sl. 3.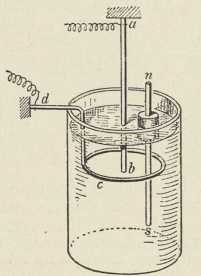 Sl. 4.
Sl. 4.Da bi se magnetom dokazala kontinuirana vrtnja magnetskog pola oko pravčaste struje, potrebno je što većma umanjiti suprotni okretni momenat struje na drugi pol magneta. Takvu vrtnju je najprije dokazao Faraday (1821). Danas se taj Faradayev pokus pokazuje variantama aparata, kakav su nekako istodobno opisali (1825) Sturgeon i G. F. Pohl (sl. 3). Dva jednaka magneta s istoimenim polovima na istoj strani obješena su unutar kružnog žlieba sa živom pomoću držaka, koje nosi bakreni štapić db; ovaj je svojim donjim zašiljenim krajem u dodiru sa živom u čašici e. Od štapića db radialno izlazi savijena žica, koja je svojim krajem malo uronjena u živi u žliebu. Struja kroz stupčić ae djeluje na južne polove ss1, pa za smjer struje cae magneti dolaze u vrtnju smjerom kazala na uri, ako gledamo odozgo. — Možda uvjerljivije djeluje varianta ovog pokusa prikazana u sl. 4. U posudi je raztopina za pobakrivanje. Magnetski štap (pletača igla) ns pliva okomito pomoću čepa od pluta. Pustimo li struju, magnet dolazi u kružnu vrtnju oko žice ab.
2. Djelovanje magnetskog polja na struju. Magnetski pol djeluje na elemenat struje jednakom i obrnutom silom Biot-Laplaceova zakona (Laplace, 1821). Međutim ove dvie sile, zbog različitih hvatišta, ne odgovaraju zakonu akcije i reakcije, već, ako su magnetski pol i elemenat struje u čvrstoj vezi, one daju par sila.
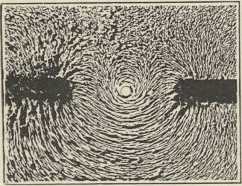 Sl. 5. Magnetske silnice pravčaste stalne struje
Sl. 5. Magnetske silnice pravčaste stalne struje
među suprotnim magnetskim polovimaSl. 5 prikazuje promjenu u obliku polja magnetskih silnica među suprotnim polovima magneta, između kojih, okomito na ravninu slike, prolazi žica sa stalnom strujom. Homogeni magnetski tok gustoće B djeluje na ravan vodič dužine l, kroz koji teče jakost struje i, silom F = Bl'i dina, gdje je l' = l • sin φ projekcija vodiča na okomicu na pravac magnetskog toka, a φ je kut između pravca vodiča i pravca magnetskog toka. Sila je uperena okomito na projekciju l′ i na pravac magnetskog toka. Za φ = 90°, t. j. kad je pravac vodiča okomit na magnetski tok, smjer se sile određuje Flemingovim pravilom lieve ruke: razkreče li se palac, kažiprst i srednjak lieve ruke pod pravim kutovima, pa se kažiprst stavi u smjer magnetskog toka, a srednjak u smjer struje, palac pokazuje smjer gibanja vodiča. To pravilo vriedi i za l' u obćenitijem slučaju φ 90°.
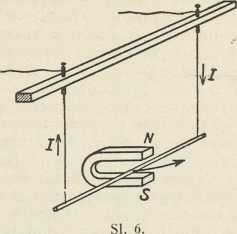 Sl. 6.
Sl. 6.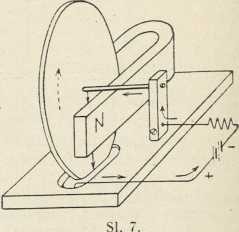 Sl. 7.
Sl. 7.Ovakvo vladanje vodiča pod stalnom strujom u magnetskom polju pokazuje se ravnom žicom bifilarno obješenom o gibkim žičnim pletenicama među polovima podkovičastog magneta (sl. 6). Kad uklopimo struju, žica se, već prema smjeru struje i smjeru magnetskog polja, trgne iz podkove ili uleti dublje u nju. Na tome se temelji Barlowljevo kolo (Barlow, 1823), okrugla kovna ploča, koja se može vrtjeti oko osi kroz središte, i kojoj je donji rub malo uronjen u živu, među polovima magneta (sl. 7). Kolo dolazi u vrtnju, ako uklopimo struju; za smjer struje elektrona, označen na slici, izprekidana strjelica pokazuje smjer vrtnje kola. — Na ovom djelovanju magnetskog polja na struju osniva se galvanometar s niti (Einthoven, 1903), koji je stariji oblik elektrokardiografa.
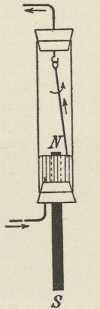 Sl. 8. Faradeyev
Sl. 8. Faradeyev
pokus Sl. 9. Davyjev
Sl. 9. Davyjev
pokusGibanje vodiča pod strujom u magnetskom polju prvi je dokazao Faraday (1821) uređajem, koji se kadkada naziva Faradayevim njihalom; u sl. 8 taj je uređaj prikazan u novijem obliku. Pošira staklena ciev dolje je začepljena čepom, kroz koji prolazi sjeverni kraj jednog magneta. Iznad čepa je nešto žive, koja je spojena pomoću žice kroz čep s jednim polom izvora struje. Živu dodiruje platinska žica, gibko obješena o gornjem čepu i spojena kroza nj s drugim polom izvora struje. Pusti li se struja kroz aparat, platinska žica dolazi u brzu vrtnju. Prema Flemingovu pravilu označenom smjeru struje u žici odgovara smjer vrtnje žice, koji pokazuje svinuta strelica. Ovom Faradayevu pokusu analogan je pokus A. De La Rivea (1848) s Geisslerovom cievlju, gdje ionska struja (pozitivni stup u cievi) rotira oko glave magneta, koji djelomice ulazi u ciev. Ovamo ide i odklon električkog luka među ugljenovima u magnetskom polju (Davy, 1921).
 Sl. 10. Ampèreov pokus
Sl. 10. Ampèreov pokusSlično i živa u posuditi na glavi jednog magneta dolazi u vrtnju oko žica, kojima se u nju uvodi i iz nje izvodi struja (sl. 9; Davyjev pokus, 1823). Takva vrtnja nastaje u analognom uređaju i u elektrolitičkim tekućinama, gdje se dakle radi o ionskim strujama.
U Ampèreovu pokusu (1822) dolazi cilindrički magnet u trajnu vrtnju oko svoje osi pod djelovanjem struje, koja teče kroza nj između njegove osi i područja oko njegova ekvatora (sl. 10). Magnet je okomito namješten među ležajevima pomoću dva šiljka, koji izlaze iz oba kraja njegove osi, a spojen je u krug struje pomoću žive u čašici k izpod njegove donje osovine i pomoću savijene žice iz c, koja malo uronjuje u živu u kružnom žliebu ff. Ovdje je kovina magneta Barlowljevo kolo za unutrašnji magnetni tok magneta. Okretni momenat kod jakosti struje i iznosi: M = i/2π∙Φ, umanjen za suprotni okretni momenat od vanjskog magnetskog toka obuhvaćenog vanjskom dovodnom žicom, koja ide iz c do žive u žliebu; ovaj subtrahend dakako odpada u uređaju, gdje struja izravno ulazi u jedan uzak pojas na plaštu magneta kroz vodljivu tekućinu. Φ je unutrašnji magnetski tok, obuhvaćen bilo kakvom čunjastom plohom između jedne točke na osi kao vrha plohe i horizontalnog obsega magneta kroz ulaz struje kod c. Smjer okretnog momenta isti je za smjerove struje nc ili sc, a odgovara Flemingovu pravilu, primienjenu na unutrašnji magnetski tok i na struju u horizontalnom presjeku magneta položenom kroz c. Isto toliko (bez subtrahenda) iznosi okretni momenat u Faradayevu pokusu iz sl. 8, ako tu Φ znači vanjski magnetski tok magneta obuhvaćen pomičnom žicom između njezina objesišta i dodirne točke sa živom u jednom okretu, a oba su okretna momenta istosmjerna za jednaki smjer struje u žici i u magnetu prema osi magneta.
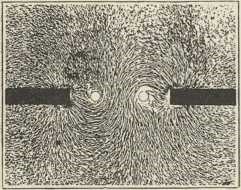 Sl. 11. Magnetske silnice stalne
Sl. 11. Magnetske silnice stalne
kružne struje među suprotnim
magnetskim polovimaZbog zavisnosti smjera sile, kojom magnetsko polje djeluje na struju, o smjeru struje kružni vodič pod stalsilnica takva kruga u magnetskom polju okretni momenat. Na to upućuje i oblik silnina takva kruga u magnetskom polju među polovima magneta (sl. 11). Na tome se temelje galvanometar s pokretnim okvirom i oscilograf s petljom.
3. Uzajamno djelovanje dviju struja. Zakon o međusobnom djelovanju paralelnih i antiparalelnih struja našao je Ampère (1820): paralelne se struje privlače, a antiparalelne se odbijaju. Dvie godine kasnije on je obradio ovo djelovanje teoretski, pa je postavio svoj elementarni zakon za silu f, kojom uzajamno djeluju dva elementa ds i ds' struje; taj zakon je kadkada nazivan Ampèreovim temeljnim zakonom elektrodinamike. Ampèreova formula glasi:
\(\qquad\qquad\displaystyle f=-C\cdot\cfrac{ii'\cdot d{\rm s}\cdot ds'}{r^2}\cdot(cos\,\varepsilon-\frac32cos\,\theta\cdot cos\,\theta').\)
Ovdje su: i, i' jakosti struje u elementima ds i ds', r je spojnica sredine elemenata, θ i θ' su kutovi, koje ds i ds' zatvaraju sa spojnicom r, a ε je kut, koji ds i ds' zatvaraju međusobno, ako jedan paralelno projiciramo na drugi. Konstanta C = 1, ako se i i i' izraze u Ampèreovoj elektrodinamskoj jedinici jakosti struje, koja je √2 puta manja od elektromagnetske cgs-jedinice jakosti. Ovaj Ampèreov zakon kao i drugi elementarni zakoni, koji su kasnije postavljeni (Grassmann, Clausius, W. Weber), imaju danas samo poviestnu vriednost. Stefan je pokazao (1869), da se dade postaviti bezbroj elementarnih zakona, koji za zatvorene struje daju iste rezultate.
 Sl. 12.
Sl. 12.Uzajamno privlačenje i odbijanje paralelnih i antiparalelnih struja pokazuje se na Ampèreovu stalku, ako jednoj stranici okvira (→ Ampèreov stalak, sl. 1) primaknemo žicu, ili stranicu jedne okvirne uzvojnice, u paralelnom, dotično u antiparalelnom smjeru struja. Privlačenje paralelnih struja dade se pokazati i pomoću dviju dugih gibkih žičnih pletenica u međusobnom razmaku oko 1 cm, kroz koje na kratko vrieme pustimo struju od 10 do 20 ampera. Isto tako, duga i uzka petlja od takve gibke pletenice, koja visi poput uzkog slova U, razširi se pod djelovanjem suprotnih struja u krakovima. U tome se očituje jedno obće svojstvo zatvorenih ravnih krivulja struje, da one nastoje obuhvatiti najveći mogući magnetski tok u što homogenijoj gustoći, tako da bi konačni oblik deformirane krivulje bio krug. Kod kruga su ove odbojne sile upravljene radialno.
 Sl. 13.
Sl. 13.I slika magnetskih silnica dvostrukog paralelnog voda upućuje na međusobno privlačenje paralelnih struja (sl. 12); isto tako slika magnetskih silnica antiparalelnih struja upućuje na njihovo međusobno odbijanje (sl. 13). Na međusobnom privlačenju paralelnih struja osniva se stezanje Rogetove uzvojnice (Roget, 1835; sl. 14). U čašici izpod uzvojnice je živa. Kad proteče struja, uzvojnica se stegne, pa njezin donji kraj izađe iz žive. Tim se struja prekine, uzvojnica se produži i uzpostavi spoj sa živom; tako ona dolazi u titranje i može se upotrebiti kao prekidač za slabije struje.
Privlačenje paralelnih struja postoji i kod trakova iste struje u elektronskom vodiču: plitak sloj žive u žliebu od izolatora suzi se, ili se čak prekine, kod gustoća struje od nekoliko stotina ampera/cm2 (Northrupov pokus, 1907). Na sličan način međusobno elektrodinamsko privlačenje elektrona u brzom paralelnom gibanju jedan je od uzroka, da se elektroni u mlazu katodnih zraka iz ravne katode ne razilaze uzprkos međusobnom elektrostatičkom odbijanju.
 Sl. 14. Rogetova
Sl. 14. Rogetova
uzvojnica Sl. 15.
Sl. 15.Dva pomična vodiča pod strujom, koji zatvaraju međusobno neki kut, teže da se namjeste tako, da struje u njima imaju isti smjer. Zato se krivudava gibka žična pletenica pod jakom strujom izpravlja. Ta se težnja napose očituje kod dviju kružnih struja, od kojih je jedna pomična, a koje su u malenom razmaku jedna od druge ili su jedna u drugoj. One nastoje namjestiti se paralelno tako, da njihova magnetska polja imaju isti smjer. Primjenom načela multiplikacije to se najbolje pokazuje ukrštenim uzvojnicama od Ritchiea (1834) prikazanim u sl. 15 u varianti od Garthea. Unutrašnja uzvojnica lako je okretljiva oko vertikalne osi; njezin spoj sa strujom ide kroz dvie plitke polukružne čašice sa živom odieljene nizkom drvenom pregradom. Pod strujom unutrašnja se uzvojnica okrene tako, da struje u njoj teku istim smjerom kao u vanjskoj uzvojnici. To je prauzor elektrodinamskih mjeraćih sprava. Nizka drvena pregrada među čašicama sa živom leži paralelno s ravninom vanjske uzvojnice; ako se unutrašnja uzvojnica zakrene s dovoljno zamaha, da svojom uztrajnošću svlada trenje kontakta u prielazu iznad gornjih rubova pregrade i zaleti se preko paralelnog položaja, kontakti uzpostave kroz živu obrnuti smjer struje u njoj, pa ona dođe u trajnu vrtnju. Tako je Ritchieov aparat najstariji model elektromotora.
Ovakvo paralelno namještanje kružnih struja bilo je podlogom Ampèreovoj teoriji magnetizma (→ elektromagnetizam). — Valja pripomenuti, da se svi ovi pokusi o međusobnom djelovanju struja mogu izvesti i pomoću izmjenične struje.M. K.
 Sl. 1. Voltin elektrofor
Sl. 1. Voltin elektrofor
(izvorna slika)Elektrofor je sprava za dobivanje veće množine električkog naboja. Sastavni dielovi: 1. kolač (Kuchen, gâteau, cake), t. j. ploča od izolatora na kovnoj podlozi ili armaturi; 2. poklopac ili štit s držkom od izolatora. Kolač je okrugla izglađena ploča od ebonita ili od šelaka, kojem je, da ne izpuca, dodano voska, terpentina i kolofonija. Poklopac je šuplje kovno tielo sa zaobljenim rubom. Kao armatura služi ravni limeni tanjur ili drvena ploča obložena staniolom ili limom. Udaramo li lisičjim repom po kolaču, postaje on negativno električan. Ako se sad na nj stavi poklopac, nastaje radi influencije na donjoj strani pozitivan, a na gornjoj negativan naboj. Taj se naboj prstom odvodi u zemlju. Dignemo li zatim poklopac, možemo njegov pozitivni naboj predati nekom tielu, na pr. lajdenskoj boci. Postupak se može mnogo puta ponoviti bez ponovnog elektriziranja kolača.
Energija naboja, koji daje elektrofor, ekvivalentna je mehaničkoj radnji, koja se vrši svladavanjem privlačne električne sile, kada dižemo poklopac. Povoljno utječe i kovna podloga, jer svojim pozitivnim nabojem prieči izbijanje kolača u zrak, kad je poklopac dignut. Promjer ploča elektrofora iznosi obično 30 do 50 cm. Gradili su velike elektrofore s promjerom od 2 m. Za dizanje poklopca upotrebili su kolotur. U suhom uzduhu zadržava elektrofor svoj naboj mjesecima. Izumilac elektrofora A. Volta (1775) nazvao je ovu spravu elettroforo perpetuo. Sl. 1 pokazuje izvorni oblik Voltina elektrofora.
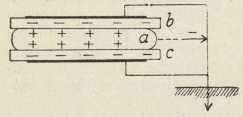 Sl. 2. Shema za složeni eektrofor
Sl. 2. Shema za složeni eektrofor Sl. 3. Složeni elektrofor
Sl. 3. Složeni elektroforNovi oblik elektrofora načinio je H. Wommelsdorf (1923). Njegova sprava (sl. 2) sastoji se od kovne ploče a i dviju ebonitnih ploča b, c. Njihove armature spojene su žicom i vezane sa zemljom. Kod eksperimentiranja treba najprije ebonitne ploče trenjem elektrizirati, među njih dovesti ploču a i njezin slobodni naboj odvesti. Ako se sad razstave dielovi elektrofora, naboj kovne ploče je tolik, da stavlja u pogon malen elektrostatski motor. Aparat s pločama, širokim 15 cm, daje napetost 50 000 volta (iskre od 6 cm). Tehničku izvedbu Wommelsdorfova aparata pokazuje sl. 3. Ebonitna ploča b učvršćena je na cievi, koja se može sklizati po držku od izolatora. Na donjem kraju držka učvršćena je metalna ploča a.
LIT.: Le Opere di A. Volta, Milan 1926.D. P-ć.
Elektroforeza → Elektrokinetički pojavi.
Elektrokemija je nauka, koja se bavi proučavanjem onih kemijskih procesa, koji se vrše utjecajem električke struje, odnosno, kod kojih se kemijska energija pretvara u električku. Elektrokemijski procesi diele se dakle u dvie grupe: kod jednih se električka energija pretvara u kemijsku, to je t. zv. elektroliza (v.), a kod drugih se kemijskom reakcijom stvara galvanski elektricitet (v.). Od vremena L. Galvanija, koji je slučajno odkrio galvanski elektricitet (g. 1790), pa do danas razvila se e. kao znanost i primienjena je u veleobrtu do takvih razmjera, da je postala jedna od osnovnih nauka o poznavanju materije (→ atom) i jedna od važnih veleobrtnih grana kao t. zv. tehnička elektrokemija.
Temelje e-e kao znanosti udario je talijanski fizičar A. Volta (g. 1794) pronalazkom, da doticajem dviju različitih kovina nastaje električka struja. Na temelju toga napravio je svoj prvi galvanski elemenat (v.). Tek time je omogućeno iztraživanje kemijskog djelovanja električne struje tako, da su u početku 19. st. proveli Ritter i Davy prvu elektrolizu vode, a nešto kasnije (g. 1807) dobio je Davy elektrolizom raztaljenih alkalijskih klorida kovine natrij i kalij. U isto doba proučava Berzelius utjecaj električke struje na otopine anorganskih tvari te na temelju tih iztraživanja postavlja prvu elektrokemijsku teoriju valencije atoma: atomi i atomske skupine imaju dva pola, kao i magnet, od kojih je jedan nabijen pozitivnim, a drugi negativnim elektricitetom; jedan je od polova uviek jači, te je atom sam nabijen pozitivno ili negativno; od veličine tog naboja zavisi reaktivnost i valencija elementa. Novija iztraživanja potvrdila su, da valenciju atoma daje broj prisutnih elektrona u atomu, odnosno onih, koji nisu prisutni.
To prvo doba e-e izpunjeno je kvalitativnim iztraživanjima. Nagli razvitak e-e počinje s Faradayem, koji g. 1833 postavlja svoj kvantitativni zakon elektrolize i elektrokemijsku nomenklaturu, koja je i danas u upotrebi (→ elektrolitička disociacija): ioni (kationi i anioni), elektrolit, elektroda (katoda i anoda). O samoj biti iona bila su podieljena mišljenja (Grotthuss, Clausius), dok to pitanje nije riešio g. 1887 S. Arrhenius. Na temelju radova J. H. van’t Hoffa o primjeni plinskih zakona na otopine postavlja Arrhenius teoriju elektrolitičke disociacije, prema kojoj se jedan dio molekula u otopini razpada sam, bez utjecaja električne struje, na ione, t. j. pozitivnim i negativnim elektricitetom nabijene atome, odnosno atomske skupine. Tu su teoriju za jake elektrolite upodpunili Debye i Hückel.
Kvantitativni odnos pretvorbe kemijske energije u električku i obratno dali su Gibbs (g. 1878) i v. Helmholtz (g. 1882) poznatom formulom: E = Q/n.23063 + T dE/dT, t. j. iz reakcione topline (Q) i temperaturnog koeficienta (dE/dT) može se izračunati elektromotorna sila nekoga galvanskog članka poznavajući kemijsku reakciju, koja se u dotičnom članku vrši. U Daniellovu galvanskom članku na pr. stvara se električna energija kemijskom reakcijom otapanja cinka, odnosno izlučivanja bakra: CuSO4 + Zn = ZnSO4 + Cu. Dobivena električka energija mora biti jednaka kemijskoj energiji. Kako je elektroliza reverzibilni proces stvaranja galvanskog elektriciteta, može se iz ove formule izračunati i ona najmanja napetost na elektrodama, koja je potrebna, da uobće dođe do izlučivanja tvari.
Sam mehanizam uzajamnog odnosa kemijskih i električkih pojava raztumačen je tek fundamentalnom teorijom elektrolitičkog tlaka otapanja od W. Nernsta (g. 1889). Prema toj teoriji nastoji svaki metal slati svoje atome kao ione u otopinu. Silu, kojom kovina šalje ione u otopinu, nazvao je Nernst »elektrolitičkim tlakom otapanja«. Taj je »tlak« za svaki metal značajan. Uroni li se na pr. komad cinka u otopinu cinkova sulfata, slat će cink svoje atome kao pozitivno nabijene ione cinka u otopinu (v. sl.). Na taj se način nabije kovina cink negativno. Radi elektrostatskog privlačenja negativno nabijenog cinka ne mogu pozitivno nabijeni cinkovi ioni difundirati u otopinu, već se stvori oko kovine na graničnoj površini metala i otopine dvostruki električki sloj. Količina iona, koje šalje metal u granični sloj, bit će to veća, što je primarno manje iona u otopini, t. j. što je manji ozmotski tlak otopine. Ozmotski tlak djeluje dakle nasuprot elektrolitičkom tlaku otapanja. Električki naboj metala (E) ovisit će dakle o veličini elektrolitičkog tlaka otapanja (P) i ozmotskog tlaka iona kovine u otopini (p) prema Nernstovoj formuli: E = RT/nF • lnP/p. Ako je elektrolitički tlak otapanja kovine veći od ozmotskog tlaka iona u otopini (P > p), a to je kod t. zv. neplemenitih kovina (na pr. aluminij, cink, olovo), onda se kovina nabije negativno. Ako je obrnuti slučaj (P < p), kao kod plemenitih kovina (na pr. bakar, srebro, zlato), onda se pozitivno nabijeni ioni iz otopine talože na kovini i nabiju je pozitivno. Kako je ozmotski tlak iona u otopini (p) proporcionalan njihovoj koncentraciji (c), t. j. E = RT/nF • lnP/k • c, to je potencial metala i prema otopini svojih iona koncentracije »l« jedna konstantna vriednost, t. zv. normalni potencial (E0) i E0=±RT/nF • lnP, gdje predznak — dolazi, ako se stvaraju pozitivni ioni, a predznak +, ako se stvaraju negativni ioni. Potencial elektrode prema otopini iona koncentracije »c«, t. zv. pojedinačni potencial, dakle je: EP=E0±RT/nF • lnc, gdje predznak + dolazi, ako elektroda šalje u otopinu pozitivne ione, a — negativne. Elektroda, uronjena u otopinu svojih iona molarne koncentracije, zove se normalna elektroda (»vodikova elektroda«, »živina ili kalomel-elektroda« i t. d.). Poredaju li se normalni potenciali metala s obzirom na vodikovu elektrodu kao jedinicu, dobiva se poznati elektrokemijski red napetosti: K, Ca, Al, Mn, Zn, Fe, Cd, Co, Ni, Sn, Pb, H2, Cu, Hg, Ag, Au. Što je kovina više nalievo, to je elektropozitivnija, t. j. to će se na katodi (negativnom polu) teže izlučiti, odnosno, trebat će to viša napetost. Minimalna napetost, potrebna da dođe do raztvaranja tvari elektrolizom, naziva se u e-i napetošću raztvaranja (Le Blanc, 1891) i može se izračunati iz gornje Nernstove formule, što je od velike važnosti za elektrolizu. Napetost raztvaranja jednaka je naime razlici pojedinačnih potenciala tvari, koje stvaraju katione i anione. Pretvaranje dakle električke energije u kemijsku (elektroliza) i obratno (galvanski elektricitet) vezano je na postojanje iona. To su dva reverzibilna procesa: jedinica količine struje (1 farad = 96500 kulona) izlučuje iz otopine jedan gram-ekvivalent iona, a isto tako prielazom jednog gram-ekvivalenta tvari u ionsko stanje nastaje ista količina elektriciteta. Prema tome je osnova ciele elektrokemije promjena stanja električkog naboja atoma, iona, odnosno atomskih skupina.
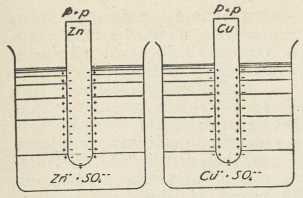 Elektrolitički tlak otapanja
Elektrolitički tlak otapanjaPrimjena elektrokemijskih procesa u tehnici vrlo je velika, a omogućena je pronalazkom dinamo-stroja od Grammea (g. 1872) kao jeftinog izvora velike količine električne energije. Od tog doba počeo je nagli razvoj tehničke elektrokemije (→ elektroliza).
LIT.: M. Le Blanc, Lehrbuch der Elektrochemie, 12. izd., Leipzig 1925; F. Foerster, Elektrochemie, 4. izd., Leipzig 1923; G. Grube, Grundzüge der Elektrochemie, 2. izd., Dresden-Leipzig 1930.I. F-ć.
Elektrokinetički pojavi očituju se u tom, da električka struja izvodi mehanička gibanja na granici tekućine i čvrstog tiela (odnosno tekućine i plina) kao i u tom, da ovakvo gibanje daje električku struju. Možemo razlikovati 3 skupine ovakvih pojava: 1. električka struja pokreće tekućinu među čvrstim stienama; 2. električka struja pokreće u mirnoj tekućini suspendirane krute, tekuće i plinovite čestice od dielektrikuma ili od vodiča; 3. gibanjem tekućine među čvrstim stienama ili gibanjem stranih čestica u tekućini nastaje elektromotorna sila. Ne postoji jedinstvena terminologija ovih pojava. Pojav (1), koji podsjeća na ozmozu, zove se obično elektroozmoza ili elektroendozmoza, a pojav (2) kataforeza. U novije vrieme uvodi se za pojave (1) i (2) zajedničko ime elektroforeza. Prema tome, da li tekućina ili suspendirane čestice putuju prema katodi ili prema anodi, zove se onda pojav kataforeza odnosno anaforeza. Za pojav (3) postoje nazivi struja strujanja, kataforetska struja. Izraz elektrokinetika dolazi i u posve drugčijem značenju, gdje se radi o elektrodinamskim i nekim elektromagnetskim učincima električke struje.
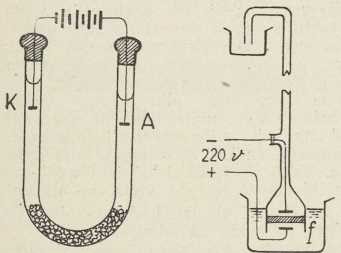 Sl. 1. Elektroosmoza vode kroz šupljikavi čep
Sl. 1. Elektroosmoza vode kroz šupljikavi čep
Sl. 2. Dizanje vode kataforezom1. Sl. 1 pokazuje jednostavan pokus o elektroozmozi. U sredini U-cievi, koja je napunjena vodom, nalazi se šupljikavi čep, na pr. od vate. Ako se na elektrode A,K stavi električka napetost, opaža se dizanje vode na strani katode. Pojav je u skladu s Coehnovim zakonom: ako se dotiču dva dielektrička sredstva (dvie »faze«), onda sredstvo s većom dielektričkom konstantom na mjestu doticaja dobiva pozitivan, a drugo sredstvo negativan naboj. Čestice vode, koja ima veću dielektričku konstantu nego čep, putuju prema katodi. Djelovanjem kataforeze može se voda kroz jenski stakleni filtar (f) dići više metara visoko (sl. 2), ako se na elektrode stavi napetost, na pr. 220 volta.
U svinutoj staklenoj cievi, koja je napunjena vodom, neka se nalazi nešto prašine od stakla ili gline. Ako se na elektrode stavi električka napetost, prašina će putovati prema anodi (anaforeza).
Jedan pokus za struju strujanja pokazuje sl. 3. Ako se na jenski filtar (f) odozgo tlači voda, a odozdo siše zrak, na elektrode priključen galvanometar (g) pokazuje struju, koja ima isti smjer kao struja tekućine.
Elektrokinetički pojavi zavise o sredstvima, koja se dotiču. Ako se mjesto vode upotrebi terpentinsko ulje, benzol, CS2, u sl. 2, 3 naznačeni pojavi, koji nastaju doticajem stakla i tekućine, teku protivnim smjerom. Bilo je više priedloga, da se elektrokinetički pojavi praktički izkoriste. Pokusi sa sušenjem treseta nisu dali očekivana uspjeha, jer primiešana voda previše vodi električku struju. Bolje služi ova metoda kod sušenja gline i kaolina u svrhe keramike te kod dobivanja kaučuka iz mliečnog soka kaučukovca.
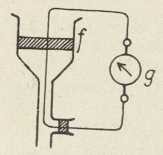 Sl. 3. Pokus za struje strujanja
Sl. 3. Pokus za struje strujanja2. Neke elektrokinetičke pojave opazio je već F. Reuss (Moskva, 1807). Točnije su ih iztražili G. Wiedemann (1852) i Quincke (1861). Za elektroozmozu izveo je Wiedemann empirijski zakon: množina tekućine, koja prolazi kroz šupljikavu diafragmu, razmjerna je s jakosti električke struje, a nezavisna o presjeku i dužini diafragme. Za struje strujanja, koje nastaju prodiranjem tekućine kroz diafragmu, našao je Quincke zakon: elektromotorna sila je razmjerna izvršenom tlaku, a nezavisna o površini i debljini diafragme.
3. Tumačenje elektrokinetičkih pojava potječe od Quinckea. On je prvi predpostavio, da se na granici čvrstog tiela i tekućine nalazi električki dvostruki sloj, koji ima na jednoj strani pozitivan, na drugoj negativan oblog. Na pr. staklenu stienu cievi dotiče čvrst negativan, a vodu gibljiv pozitivan oblog sloja. Djeluje li na sloj vanjska električka sila, pomiče se gibljiv dio sloja i povlači trenjem tekućinu. To daje pojav elektroozmoze. Ako se pak kroz staklenu ciev tjera tekućina, dovodi se jednoj elektrodi pozitivan, a drugoj preostaje negativan naboj.
Teoriju ovih pojava formulirao je matematički najprije Helmholtz (1879). Polazeći od hidrodinamskih jednačbi, uz predpostavku, da su crte strujanja uzporedne s osi kapilarne cievi, izveo je H. za brzinu tekućine formulu
\(\qquad\qquad\displaystyle v=v_0+\cfrac{^vi\;\sigma\;\varepsilon}{4\;\pi\;\eta}(\varphi-\varphi')\)
U toj formuli znači v0 brzinu, koju bi dao sam prirast hidrostatskog tlaka (bez električkog polja), i jakost električke struje, σ specifički električki odpor tekućine, ε dielektričku konstantu tekućine, η nutrašnje trenje tekućine, φ—φ’ potencialnu razliku među oblozima dvostrukog sloja (elektrokinetički potencial).
Pomoću mnogih teorija nastojali su protumačiti prirodu dvostrukog sloja. Coehn i Raydt su našli, da spomenuti Coehnov zakon vriedi i kvantitativno. Visina dizanja tekućine je uviek razmjerna razlici dielektričkih konstanata sredstava, koja su u doticaju.
Ako se dielektrička tekućina načini slabim elektrolitom, elektrokinetički pojavi postaju zamršeniji. Električka vodljivost se superponira na dielektrička svojstva tekućine. Dodatkom neznatne količine elektrolita može dvostruki sloj izmieniti polaritet. Prema ozmotičkoj teoriji bio bi elektrokinetički potencial identičan s elektromotornom silom, koja nastaje radi Nernstove napetosti otapanja (Lösungstension). Eksperimentalni rezultati ne slažu se s ovom teorijom. Nernstov skok potenciala iznosi ciele volte ili nekoliko desetinski volta, dok se kod elektrokinetičkih pojava radi o napetostima od nekoliko stotinaka volta. Freundlich tumači ove pojave teorijom adsorbcije (1909), a Gony i Chapman difuzijom. Ove teorije rade s dva sloja. Jedan sloj je vrlo tanka kožica tekućine, koja se čvrsto drži stiene, a drugi susjedni sloj seže dublje u tekućinu. Dolazi do superpozicije dvaju elektrokinetičkih potenciala. Sa sličnim predpostavkama rade i novije teorije, koje su razvili O. Stern (1924), Debye i Hückel (1924).
LIT.: Graetz, Hdb. d. Elektrizität u. d. Magnetismus II., 1921; Geiger u. Scheel, Hdb. d. Physik XIII., 1928; Müller-Pouillet, Lehrbuch d. Physik, 11. izd., IV., 1934.D. P-ć.
Elektrolitička disociacija je razpadanje molekula u vodi otopljene tvari na ione, t. j. na pozitivnim ili negativnim elektricitetom nabijene atome odn. na atomske skupine. Od količine električkog naboja ovisi valencija iona. Tako se na pr. razpada (disociira) natrijev klorid (NaCl) otapanjem u vodi na pozitivne natrijeve ione (Na+) i negativne klorove ione (Cl-); sumporna kiselina (H2SO4) daje u vodenoj otopini dva jednovalentna vodikova iona (H+) i jedan dvovalentni sulfat-ion (SO4—); aluminijev klorid daje trovalentni aluminijev ion i tri klorova iona, što se grafički prikazuje ovako: AlCl3 Al+ + + 3Cl-. Tvari, koje daju ione, zovu se elektroliti (soli, kiseline i baze), jer njihove vodene otopine vode električku struju (→ elektroliza). Transport struje vrše ioni (ἐῶν »putujući«), i to pozitivno nabijeni ioni, kationi, kreću se prema negativnoj elektrodi (katodi), a negativni ioni, anioni, prema pozitivnoj elektrodi (anodi).
Prema S. Arrheniusu, koji je postavio teoriju e-e d-e (g. 1887), disociira se samo jedan dio molekula u ione, te prema jakosti disociacije razlikujemo jake (NaCl, KNO3, H2SO4, KOH i t. d.) i slabe elektrolite (H3BO3, H2CO3, NH4OH, HgCl, i t. d.). Razređenjem otopine raste disociacija. Omjer disociiranih i nedisociiranih molekula je stupanj disociacije (a), koji je dakle proporcionalan ozmotskom tlaku i električkoj vodljivosti (λ) otopine elektrolita. Za jednu stanovitu koncentraciju elektrolita (c) je disociacija konstantna i izražava se konstantom disociacije, Kc = c • α2/(l — α), ili Kc = c • λ2/λ∞ (λ∞ — λ) (Ostwaldov zakon razređenja, gdje je λ∞ vodljivost kod neizmjernog razređenja). Izpitivanjima je utvrđeno, da se kod jakih elektrolita ne dobivaju konstantne vriednosti za konstantu disociacije. Za razjašnjenje tih i drugih anomalija kod jakih elektrolita upodpunili su Debye, Hückel (1923) i Onsager (1927) Arrheniusovu teoriju time, što su postavili, da su jaki elektroliti podpuno disociirani. Radi velikog broja suprotno nabijenih iona dolazi do međusobnog elektrostatskog privlačenja, do izvjestnog vezanja negativnih iona na pozitivne, tako da se jedan stanoviti pozitivni ion nalazi bliže nekom negativnom nego drugom pozitivnom ionu. Posljedica toga je opadanje pokretnosti (brzine) iona s povećanjem koncentracije elektrolita, a time i električke vodljivosti, što se prije pripisivalo smanjenju disociacije. Radi tih međuionskih sila aktivna količina nekog iona, aktivitet (a), nije identična s koncentracijom (c), već manja i izražava se sa: a = f∙c, gdje je f koeficient aktiviteta, koji se s povećanjem razređenja približuje vriednosti 1.
Sposobnost vode, da raztvara elektrolite u ione, jest u tome, što je voda izvanredno jaki dielektrikum (v., DK = 81), t. j. smanjuje elektrostatska privlačenja elektropozitivnih i elektronegativnih dielova molekula stvarajući tako slobodne pozitivne i negativne ione:
kation│ voda │anion.
LIT.: H. Falkenhagen, Elektrolyte, Leipzig 1932; W. Kuhn, Physikalische Chemie, Leipzig 1942.I. F-ć.
Elektrolitička polarizacija → Elektroliza.
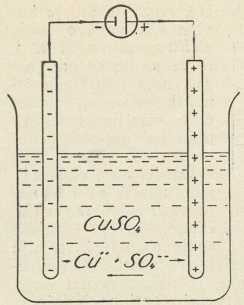 Sl. 1. Elektroliza CuSO4
Sl. 1. Elektroliza CuSO4Elektroliza je raztvaranje ili obćenito kemijsko mienjanje neke tvari pomoću električke struje. Tvar, koje otopina ili taljevina vodi električku struju, a kod toga se kemijski mienja, zove se elektrolit. Polovi, kojima se dovodi električka struja, jesu elektrode, i to negativni je pol katoda, a pozitivni anoda. Čestice tvari, atomi, odnosno atomske skupine, koje tokom e-e putuju k elektrodama, zovu se ioni, i to k negativnom polu kreću se pozitivno nabijeni kationi, a k pozitivnom negativno nabijeni anioni (→ elektrolitička disociacija). Najvažniji elektroliti jesu kiseline (HCl, H2SO4 i dr.), lužine (NaOH, KOH, i t. d.) i soli (KCl, NaCl, NH4NO3, CuSO4, AgNO3, Na2CO3 i t. d.). Pozitivno nabijeni ioni, kationi, jesu svi ioni kovina, vodikov i amonijev ion (H+, NH4+, K+, Na+, Ag+, Mg++, Cu++, Al+ + + i t. d.), dok su negativno nabijeni, anioni, kiselinski ostatci (Cl-, NO3-, SO4--, CO3- i t. d.) i hidroksilna skupina (OH-).
Elektrolizira li se između dvie platinske elektrode otopina bakrenog sulfata —CuSO4 (sl. 1), izlučit će se na negativnom polu (katodi) bakar, a na pozitivnom polu (anodi) kisik, radi sliedećih procesa na elektrodama.
1. Procesi na katodi vrše se utjecajem negativnog naboja elektrode u smislu izbijanja pozitivno nabijenih kationa i njihova pretvaranja u neutralne atome, odnosno molekule. To neutraliziranje pozitivnih naboja kationa na katodi vrše elementarni negativni djelići električke struje (→ elektroni). Gornji primjer izlučivanja bakra može se prikazati dakle ovako: Cu+ + + 2 elektrona = Cu. Procesi na katodi jesu primanje elektrona od pozitivno nabijenih iona, koje može biti takvo, da dovodi do podpune ili samo djelomične neutralizacije pozitivnih iona. Kako je oduzimanje pozitivnih naboja ionima redukcija, to su i elektrolitički procesi na katodi redukcioni procesi: izlučivanje kovina, pretvaranje viševalentnih kationa u niževalentne i redukciono djelovanje na katodi razvijenog atomarnog vodika.
2. Procesi na anodi suprotni su onima na katodi: anioni gube elektrone, t. j. negativni naboji aniona izbijaju podpuno ili samo djelomično na pozitivno nabijenoj elektrodi. Na anodi vrše se dakle oksidacioni procesi. Kod gornje elektrolize bakrenog sulfata vrši se dakle na anodi ovaj proces: SO4-— 2 elektrona = SO4. Kako SO4 -skupina ne može sama postojati, to se spaja s prisutnom vodom dajući sumpornu kiselinu, a na elektrodi se oslobađa kisik: 2SO4 + 2H2O = 2H2SO4 + O2. Ovakvi sekundarni procesi dosta su česti kod e-e. Ako se mjesto platinskih elektroda uzmu bakrene, ostat će proces na katodi, t. j. taloženje kovine, isti, ali na anodi se ne će razvijati kisik, već će se anoda otapati, t. j. kovni bakar prelazit će gubitkom elektrona kao pozitivno nabijeni bakreni ioni u otopinu: Cu — 2 elektrona = Cu++. Topljive anode jesu na pr. iz bakra, srebra, cinka, olova, kositra i t. d., a netopljive iz platine, grafita, ugljena i raztaljenog magnetita. Na anodno topljivim elektrodama dolazi više puta do iznenadnog zastoja u otapanju, t. zv. pasivnog stanja. Razlog pasivnosti može biti mehaničke (stvaranje netopljivog sloja) ili kemijske prirode (smanjenje brzine stvaranja iona).
Da uobće može doći do e-e, potrebna je na elektrodama minimalna napetost, t. zv. napetost raztvaranja (→ elektrokemija), koja je značajna za svaki elektrolit. Da i prije te napetosti ne dolazi do raztvaranja elektrolita, razlog je u t. zv. polarizacionoj napetosti, koja djeluje nasuprot napetosti na elektrodama. Ta elektrolitička polarizacija, koja djeluje nasuprot e-i, nije dakle ništa drugo nego nastojanje izlučenih tvari, da ponovno prieđu u otopinu, a to se očituje suprotnom elektromotornom silom. Uzroci polarizacije mogu biti i u nekim drugim pojavama na elektrodama: oksidacija, promjena koncentracije elektrolita na elektrodama i dr. Neki plinovi, kao vodik, kisik i klor, ne izlučuju se e-om uviek kod iste napetosti izlučivanja, već kod stanovite više napetosti (»prenapetost«, njem. Überspannung, engl. Overvoltage), koja ovisi od prirode elektrode. Tako se vodik izlučuje (iz 5%-tne H2SO4) na platinskoj elektrodi kod 0,1 volta, na olovnoj el. kod 0,5 volta, a na živinoj el. čak kod 0,8 volta. To svojstvo vodika osobito je važno za tehničku e-u.
Kvantitativni odnos između e-om izlučenih tvari i utrošene električke energije daje Faradayev zakon: za izlučivanje jednog gram-ekvivalenta (= atomska, odnosno molekularna težina u gramima podieljena s valencijom) neke tvari potrebna je količina električke struje od 96.500 coulomba = 96.500 amper-sekunda=26,8 amper-sati. Dakle, količinom struje od 26,8 amper-sati izlučit će se na katodi, odnosno otopiti na anodi: 107,88/1 = 107,88 g srebra, 63,57/2 = 31,78 g bakra, 26,97/3 = 8,99 g aluminija; isto tako izlučit će se na anodi: 35,46/1 = 35,46 g klora, 16,00/2 = 8,00 g kisika i t. d. Količina tvari, kojoj je za izlučivanje ili otapanje potrebna količina struje od jedne amper-sekunde, naziva se elektrokemijski akvivalenal: 107,88/96500 = 1,118 mg srebra, 0,3294 mg bakra, 0,3675 mg klora i t. d. U praksi se riedko dobivaju te teoretske količine, već manje, a odnos dobivene količine i teoretske količine jest izkoristivost struje, koja je kod e-e vodenih otopina 75—100%, a kod taljevina i manja.
Količina na e-u potrošene električke energije jest produkt od napetosti na elektrodama, jakosti struje, što prolazi kroz elektrolitičku stanicu, i vremena trajanja e-e.
 Sl. 2. Naprave za elektrolizu vode
Sl. 2. Naprave za elektrolizu vodePrimjena elektrolize u tehnici: elektrolitičko dobivanje i rafiniranje kovina iz otopina (→ bakar, cink, nikal i t. d.) i taljevina (→ aluminij, magnezij, natrij, kalij i t. d.), → galvanostegija i → galvanoplastika, e. vode i alkalijskih klorida, elektrolitička oksidacija i redukcija anorganskih i organskih tvari i t. d.
Elektroliza vode. Raztvaranje vode na vodik i kisik osniva se na izbijanju vodikovih iona na katodi: 2H+ + 2 elektrona = H2, i hidroksilnih iona na anodi: 2 OH— —2 elektrona = H2O + O. Kako sama voda praktički ne vodi električku struju, dodaje joj se elektrolita, obično kalijske ili natrijske lužine (20 do 25%). Za 1 m3 vodika potrebno je praktički 4,5—5 kilovat-sati. Dobiven elektrolitski vodik ima čistoću 99,9%, a kisik 99,6—99,8%.
Vodik služi za sintezu amoniaka, hidriranje masti i drugih tehničkih produkata i t. d. Sama e. vode vrši se s dvie vrste elektrolitičkih stanica: unipolarne (Fauser, Holmboe, Electrolabs Comp., Kent, Steward i dr.) i bipolarne (Bamag-Zdansky, Pechkranz, Siemens, Egasco i dr.). Najviše se radi s bipolarnim stanicama, u kojima anoda jedne stanice služi ujedno kao katoda sliedeće (sl. 2). Elektroda je iz željeznog lima poniklovana s anodne strane. Da ne dođe do miešanja razvijenih plinova, odieljen je anodni od katodnog prostora diafragmom, obično iz azbesta. Najveći postroj za e-u vode nalazi se u Norvežkoj, a radi po sistemu Pechkranz sa 100.000 KW.
Velike količine klora i alkalijskih hidroksida, potrebne za kemijski veleobrt, dobivaju se danas izključivo elektrolizom vodene otopine alkalijskih klorida. Na anodi razvija se iz vodene otopine na pr. natrijeva klorida (H2O + NaCl) klor (Cl), a na katodi vodik (H), dok preostali ioni natrija (Na+) i hidroksilni ioni (OH—) daju natrijevu lužinu (NaOH): anoda ← Cl- + Na+ + OH- + H+ → katoda. Proizvodi e-e jesu dakle: lužina, klor i vodik. Napetost je raztvaranja alkalijskih klorida visoka i iznosi 3,5—5 volta. Za 1 kg natrijeve lužine potrebno je oko 3 kilovat-sata. Da ne dođe do reakcije stvorenog hidroksida s klorom, odieljen je katodni prostor od anodnog, te prema načinu odjeljivanja razlikujemo 3 postupka: postupak s diafragmom, postupak sa zvonom i živin postupak. Najviše se radi po postupku s diafragmom, a zatim sa živom. Svjetska potrošnja električne energije za e-u alkalijskih klorida cieni se na koje 3 miliarde kilovat-sati.
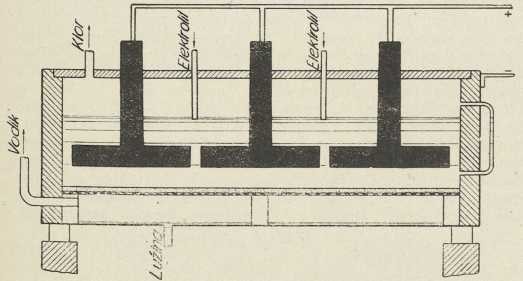 Sl. 3. Siemens-Billiterova stanica s diafragmom
Sl. 3. Siemens-Billiterova stanica s diafragmom Sl. 4. Naprave za elektrolizu otopine alkalijskih klorida
Sl. 4. Naprave za elektrolizu otopine alkalijskih klorida
(Siemens-Billiter)Kod postupka s diagfragmom odieljen je anodni prostor od katodnog poroznom stienom iz cementa ili azbesta (sl. 3). Anoda, gdje se razvija klor, iz grafita je ili raztaljenog magnetita. Katoda je željezna mreža ili iz željeznih štapova poput roštilja. Od mnogih ovakvih stanica najrazširenija je Siemens-Billiter-stanica (sl. 4) s horizontalnom diafragmom, za razliku od nekih amerikanskih stanica (Nelson, Gibbs-Vorce) s vertikalnom diafragmom.
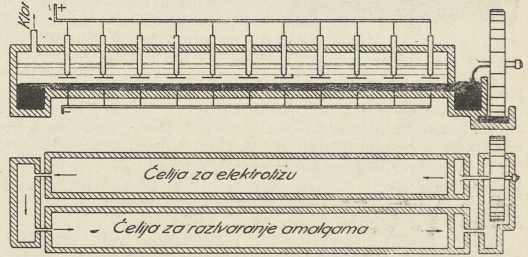 Sl. 5. Solvayeva stanica sa živom
Sl. 5. Solvayeva stanica sa živomPostupak sa živom radi bez diafragme. Ovdje služi kao katoda živa. Radi velike »prenapetosti« vodika na živinoj katodi ne dolazi do njegova izlučivanja, već do izlučivanja alkalijske kovine, koja stvara sa živom amalgam. Zato se amalgam automatski prenosi u drugi dio stanice, gdje se s vodom raztvara u alkalijski hidroksid i vodik, a čista živa ponovno odlazi u anodni prostor kao katoda. Anoda je iz platine ili grafita. Prema načinu prienosa žive i prema konstrukciji postoji više stanica (Castner, Kellner, Solvay, Wildermann, Whiting i t. d.), od kojih je dosta razširena Solvaveva (sl. 5), koja je izgrađena i do kapaciteta od 15.000 ampera. Prienos amalgama iz prostora za elektrolizu u prostor za raztvaranje vrši se na taj način, što je stanica nagnuta. Čista se živa ponovno diže u prostor za e-u s pomoću izvijaćeg kotača. Kod nas u tvornici u Jajcu radi se e. otopine natrijeva klorida po Kellnerovu postupku.
Postupak sa zvonom osniva se na činjenici, da je katodna otopina lužine specifički teža od anodne. Tako ne dolazi do miešanja katodnih i anodnih proizvoda, te je nepotrebna upotreba diafragme. Jedina je još u pogonu stanica ove vrste u Aussigu.
Ako se e. otopine alkalijskih klorida vrši bez diafragme, tako da dolazi do miešanja razvijenog klora i lužine, nastaje otopina hipoklorita, koja služi u veleobrtu za bieljenje. E-om pak kod temperature od 75°C nastaju klorati i perklorati, potrebni u veleobrtu eksploziva.
Veliko je područje primienjene e-e elektrolitička redukcija, kojom se dobivaju mnogi anorganski i organski spojevi: natrijev hiposulfit, hidroksilamin, benzidin, bieli indigo i t. d.
Nasuprot redukciji na katodi mogu se na anodi izvršiti najrazličitije elektrolitičke oksidacije: vodikov peroksid, kalijev permanganat, kalijev fericianid, perklorati, perborati i perkarbonati (sastojci prašaka za pranje, kao na pr. »Persil«), regeneriranje iztrošene otopine kromne kiseline, jodoform, octena kiselina, mnogi aromatski spojevi i t. d. Vrlo je važna primjena elektrolitičke oksidacije kod t. zv. eloksiranja. To je prevlačenje površine aluminija i njegovih legura sa slojem aluminijeva oksida s pomoću elektrolitičke oksidacije. Na taj način postaje površina kovine odporna prema kemijskim i atmosferskim utjecajima, stalna protiv vatre i lako se može bojadisati. Od mnogobrojnih postupaka (Eloxal, Scheppard, Bengough-Stuart, Alumilite, Alcoa, Seo i t. d.) najpoznatiji je Eloxal-postupak: aluminij i njegove legure ukapčaju se u krug električke struje kao anoda; kao elektrolit služi otopina, koja sadržava 3–10% oksalne kiseline i 0,1% kromne kiseline. Može se upotrebiti istosmjerna i izmjenična struja od 60—100 volta.
LIT.: R. Müller, Elektrometallurgie, Beč 1932; R. Müller, Elektrochemie nicht metallischer Stoffe, Beč 1937; Ullmann, Enzyklopädie der technischen Chemie, sv. III., 12. izd., Berlin—Beč. 1929.I. F-ć.
 Sl. 1. Katodna ciev s rudama,
Sl. 1. Katodna ciev s rudama,
koje fluoresciraju Sl. 2. Katodna luminiscencija
Sl. 2. Katodna luminiscencija
na preparatu izvan cieviElektroluminiscencija je pojav luminiscentne (hladne, fluorescentne) svjetlosti izazvan katodnim, kanalnim i Röntgenovim zrakama. Katodna luminiscencija se opaža na onim dielovima katodne cievi, na koje udaraju katodne zrake. Kod toga različna stakla fluoresciraju bojama od modre do žutozelene. Katodne zrake s malenim brzinama mogu uzbuditi crvenu fluorescenciju stakla. Pojav e-e pokazuje velik broj krutih i tekućih tvari, od kojih spominjemo Balmainovu boju (CaS), kalcijev volframat, ZnS, od ruda sfalerit, dolomit, magnezit, korund (sl. 1), a od tekućina petrolej.
Za spektralno izpitivanje katodne luminiscencije nije uviek potrebno, da se tvar nalazi u samoj katodnoj cievi. Za takve svrhe služi i ciev s Lenardovim prozorčićem (sl. 2). Kroz tanki kovni listić takva prozorčića mogu katodne zrake prolaziti i uzbuditi luminiscentnu svjetlost na preparatu izvan cievi s uređajem za grijanje. Kod viših temperatura nastaju novi dielovi vrpčastog luminiscentnog spektra.
Američki iztraživači Coolidge (1925) i Vollrath (1931) našli su, da i zrak obične gustoće intenzivno fluorescira, ako kroza nj prolaze brze katodne zrake. Ako se za pogon cievi, koja ima velik broj vrlo blizih Lenardovih prozorčića, upotrebi visoka napetost (na pr. 500 000 volta), fluorescira vanjski zrak kroz daljinu od 1 m.
Bilo je pokušaja, da se katodna luminiscencija upotrebi u svrhu električke razsvjete. Kod Ebertove luminiscentne lampice svietli je izvor puce od azbesta obasjano katodnim zrakama.
Goldstein je pokazao, da i kanalne zrake, poput katodnih, pobuđuju luminiscenciju stakla i drugih tvari (1902).
Među pojave elektroluminiscencije ubraja se i svjetlost Geisslerovih cievi, Teslina svjetlost i svjetlost Mac Farlan Moorea. Na velikom broju tvari iztraživali su ove pojave J. Becquerel, Lenard, Tomaschek, Urbain i dr.
LIT.: M. Curie, Luminiscence de corps solides, Pariz 1934; N. Riehl, Physik u. technische Anwendungen d. Luminiszenz, Berlin 1941.D. P-ć.
Elektromagnetizam u užem, običnijem smislu bavi se magnetskim poljem električke struje i njegovom primjenom za dobivanje jakih magnetskih tokova i polja. Kod nekih pisaca e. obuhvaća čitavo područje sveze između električke struje i magnetizma, pa obrađuje cieli magnetizam, elektrodinamiku i inducirane struje.
 Sl. 1.
Sl. 1.Ako iznad mirne deklinacione magnetske igle stavimo ravnu žicu pod stalnom strujom odprilike u pravcu zemaljskog magnetskog meridiana, magnetska igla se odklanja tako, da se njezin sjeverni kraj skrene prema iztoku ili prema zapadu. Smjer odklona zavisi o smjeru struje. Ako žica u jednakim prilikama prolazi izpod magnetske igle, odkloni su suprotni. To su osnovna opažanja, koja je objavio 21. VII. 1820 Oersted u Kopenhagenu. Tim je on odkrio magnetsko polje električke struje. Ampère je malo mjeseci kasnije za smjer odklona magnetske igle dao t. zv. pravilo plivača (→ Ampèreovo pravilo). Ovo se pravilo može zamieniti pravilom desne ruke: položimo izpruženu desnu ruku na žicu tako, da su prsti u smjeru struje, a dlan da je okrenut prema magnetskoj igli, onda se sjeverni kraj igle odklanja prema palcu (sl. 1).
Malo je bilo odkrića u fizici, koja bi se mogla uzporediti s ovim Oerstedovim odkrićem ne samo po važnosti, nego i po brzini, kojom su se iza njega nizale nove spoznaje i nova odkrića. Već u nekoliko mjeseci iza toga bile su odkrivene podloge elektrodinamike i elektromagnetizma. Gotovo su isto tako bile plodne i iduće dvie godine. Ovo je razdoblje bilo okrunjeno 11 godina kasnije odkrićem induciranih struja (Faraday, 1831).
Arago i Gay-Lussac su u rujnu 1820 pokazali, da se čelična igla u uzvojnici, kroz koju teče struja, trajno magnetizira. Schweigger je početkom istog mjeseca objavio svoje načelo multiplikacije magnetskog djelovanja struje time, da se struja vodi oko magnetske igle u više uzvoja. Od polovine rujna do početka studenoga nije bilo gotovo ni jedne sjednice Francuzke akademije znanosti, na kojoj ne bi Ampère prikazao nove pokuse. Osim svojih zakona o djelovanju struje na struju (→ elektrodinamika 3) on je u to doba objavio i svoj nalaz, da se uzvojnica pod strujom vlada kao magnet, pa je na temelju toga dao i osnovnu misao svoje teorije magnetizma. Ovu je potanje obradio idućih dviju godina. Arago i nezavisno od njega Yelin objavili su u studenom 1820 magnetiziranje čelične igle pomoću električke iskre iz lajdenske boce, kad su žicu od vanjskog obloga prema unutrašnjem savili u uzvojnicu i u ovu stavili iglu. Davy je istog mjeseca javio Wollastoneu, da je pomoću iskre iz jake lajdenske baterije magnetizirao kratke čelične igle, koje su ležale poprieko izpod spojne žice, te da se željezna piljevina na kartonu izpod te žice namješta okomito na pravac žice. Tim je bila utvrđena za ono doba nova važna veza između statičkog elektriciteta i galvanske struje. Sturgeon je 1825 izradio prvi podkovasti elektromagnet, a već 1828 je Moll u Utrechtu sagradio elektromagnet, težak 5 funti, koji je nosio težinu od 75 funti. Henry je u Americi za namatanje jakih elektromagneta uveo izoliranu žicu i namatanje u više slojeva (1831). Elektromagnet, koji je iste godine sagradio za Yale College, nosio je težinu od 3000 funti. Te je iste godine on u Albanyju prikazao prvi elektromagnetski brzojav. Razmjerno kasno počelo se pitanje nosivosti elektromagneta obrađivati kvantitativno; Joule (1839) je našao, da se magnetski momenat ravnog elektromagneta s porastom jakosti struje približava nekom maksimumu.
 Sl. 2. Magnetske silnice stalne
Sl. 2. Magnetske silnice stalne
pravčaste struje Sl. 3. Magnetske silnice
Sl. 3. Magnetske silnice
magnetskog listaAko kroz sredinu horizontalnog komada kartona, posutog sitnozrnom željeznom piljevinom, vertikalno provedemo dugu ravnu žicu i kroz ovu pustimo jaku stalnu struju, piljevina se uz lako kuckanje po kartonu poreda u koncentrične krugove (sl. 2). Magnetske silnice pravčaste struje su krugovi, koncentrični sa žicom, koji leže u ravnini, okomitoj na žicu; to izlazi iz Biot-Savartove formule za bezkonačno dug pravčast vodič (→ elektrodinamika 1). Iz Ampereova pravila plivača izlazi za smjer magnetskih silnica struje pravilo: ako gledamo u smjeru struje, smjer silnica je u smjeru gibanja kazala na uri. Odatle se izvodi smjer magnetskog polja za magnetski list (→ elektrodinamika 1). U slici 3 prikazano je polje magnetskih silnica magnetskog lista u ravnini, položenoj kroz njegovu os. Slika 4 prikazuje magnetske silnice jedne kratke ravne uzvojnice, a slika 5 magnetske silnice za dugu gustu pravčastu uzvojnicu. Na svakom kraju uzvojnice silnice se razilaze i savijaju k drugom njezinu kraju; u sl. 5 polje silnica već posve nalikuje polju silnica magnetskog štapa. Zbog ovog razilaženja ili razsipanja silnica u blizini se krajeva najjače očituje vanjsko mehaničko djelovanje magnetskog polja uzvojnice; zato i ovdje krajeve često nazivaju »polovima« uzvojnice. Kod zatvorene prstenaste uzvojnice daleko pretežni dio silnica prolazi kroz nju u približno konstantnoj gustoći (sl. 6); ona nema »polova«, već čini zatvoreni magnetski krug. Magnetske silnice su u svim slučajevima zatvorene krivulje.
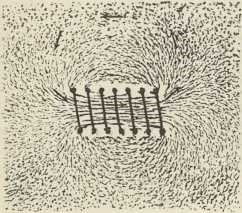 Sl. 4. Magnetske silnice kratke
Sl. 4. Magnetske silnice kratke
ravne uzvojnice Sl. 5.
Sl. 5.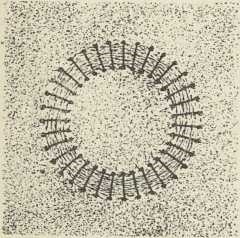 Sl. 6. Magnetske silnice
Sl. 6. Magnetske silnice
prstenaste uzvojniceRavna uzvojnica (»solenoid«), zgodno obješena, na pr. na Ampèreovu stalku (v.), namješta se pod strujom u magnetski meridian. Za polaritet njezinih krajeva vriedi isto pravilo kao za magnetski list (→ elektrodinamika 1). Primaknemo li njezinu kraju, u koji ulaze magnetske silnice, južni kraj magneta, oni se odbijaju.
Jakost magnetskog polja u osi ravne, jednoliko namotane cilindričke uzvojnice, koja je u poredbi s njezinim promjerom vrlo duga, jest: H = 4 π n i ersteda, gdje je n broj uzvoja na 1 cm dužine uzvojnice, dok je i jakost struje u elektromagnetskim cgs-jedinicama. Na samim krajevima jakost polja je polovica ovog iznosa. Područje homogenosti polja je u radialnom smjeru to šire, što je manji omjer polumjera uzvojnice prema njezinoj dužini, pa se za vrlo dugu gustu uzvojnicu može uzeti, da je polje u njoj, osim neposredne blizine krajeva, homogeno. Ova formula vriedi s dobrom približnošću i za prstenastu uzvojnicu, ako je polumjer prstena dosta velik prema polumjeru uzvoja, a n brojimo po sredini debljine prstena. Strogo homogeno magnetsko polje dobiva se u unutrašnjosti gusto namotane elipsoidalne uzvojnice, t. j. takve, koja je namotana na jednom rotacionom elipsoidu, ako na 1 cm dužine rotacione osi dolazi točno jednak broj uzvoja.
Na temelju činjenice, da je kružna struja ekvivalentna s vrlo kratkim magnetom, Ampère je postavio molekularnu teoriju magnetizma (1821, 1822), kojom je dopunio stariju teoriju elementarnih magneta. Njom je uklonjen magnetizam kao neki zaseban agens i sveden na svojstvo električke struje. Po Ampèreovoj teoriji oko molekula jedne feromagnetičke kovine vječno kruže električke struje. To su t. zv. molekularne ili elementarne struje. Dok je takva kovina u nemagnetičnom stanju, ravnine molekularnih struja leže bez reda u svim mogućim položajima, i među njima su podjednako zastupana oba smjera kruženja. Magnetiziranje kovine sastoji se u tom, da se djelovanjem vanjskog magnetskog polja veći ili manji broj ovih struja zakrene tako, da im ravnine dođu okomito na smjer polja i u isti smjer kruženja. Ova naoko tako jednostavna teorija uključivala je u sebi velike potežkoće. Osobita potežkoća bila je u predočbi struja, koje bi vječno tekle bez slabljenja zbog odpora. Nije lako bilo ni sa zamisli, koju je prvi uveo Richarz (1890), da se Ampèreove struje sastoje u kruženju Helmholtzovih elementarnih množina elektriciteta, dotično Stoneyevih elektrona. Snažnu kvalitativnu podporu dao joj je pokus, koji je zamislio i uzalud kušao izvesti Richardson (1908), a izveli su ga 1915 Einstein i de Haas (→ Einstein-de Haas-efekt). I obrnuti pokus: željezni štap u brzoj vrtnji trebao bi se zbog same vrtnje slabo magnetizirati u pravcu osi vrtnje. To su zaista pokazali pokusi, koje je izveo Barnett (1914) (→ giromagnetički pojavi). Zbog kvantitativnih razlika rezultata ovih dvaju pokusa prema onima, kakve bi trebalo očekivati po jednostavnoj teoriji, danas se uzima, da Ampèreove elementarne struje u feromagnetičkim kovinama ne stoje u kruženju elektrona, nego u vrtnji elektronskog vrtloga oko vlastite osi.
Elektromagnet. Stavimo li u uzvojnicu, kroz koju teče stalna struja, jezgru od mekog željeza, magnetizam uzvojnice se silno pojača, jer se i željezo magnetizira, pa se njegov magnetizam superponira na magnetsko polje uzvojnice. Magnetsko polje pred glavom ravne uzvojnice sa željeznom jezgrom nekoliko je stotina puta jače od magnetskog polja iste uzvojnice bez željezne jezgre kod iste jakosti struje. To je elektromagnet, u ovom primjeru ravan. Njegov magnetizam gotovo sasvim nestaje, čim prekinemo struju u uzvojnici. Na ovim svojstvima temelje se njegove mnogobrojne znanstvene i tehničke primjene. Prvi elektromagneti bili su ravni; izradio ih je po svoj prilici već Arago u početku 1821.
Osobito velika pojačanja prvobitnog magnetskog toka uzvojnice dobivaju se, ako željezna jezgra čini zatvoren magnetski krug (prstenasti elektromagnet ili toroid). To je elektromagnet bez polova, jer u njemu praktički sve magnetske silnice prolaze kroz željezo, dok ih se vrlo neznatan dio razsiplje u zračni prostor. To razsipanje zavisi o permeabilnosti željeza, a i o obliku magnetskog kruga. Zato se za gradnju osobito jakih elektromagneta upotrebljavaju meka željeza s vrlo velikom permeabilnošću; osim toga traži se od takva željeza, da ima što manji remanentni magnetizam. U novije se vrieme pojedini važniji dielovi velikih elektromagneta grade od slitine željeza sa 34% kobalta, jer ima veću permeabilnost od najboljega mekoga željeza.
Način namatanja uzvojnice raznolik je, i to prema obliku i zadaći elektromagneta. Kod ravnih elektromagneta uzvojnica pokriva gotovo cielu dužinu željezne jezgre, a namotana je u više slojeva. Kod podkovastih elektromagneta uzvojnica je namotana oko krakova, rjeđe i oko spojnog diela (jarma), a kod prstenastih oko cielog prstena ili oko dva diela, koji simetrično leže. Kako je mjerodavan produkt broja uzvoja s jakošću struje, izbor broja uzvoja načelno zavisi s jedne strane o jakosti razpoložive struje, da bi se željezo magnetiziralo blizu do zasićenosti, a s druge strane o gornjoj granici zagrijavanja uzvojnice Jouleovom toplinom. Kod vrlo jakih elektromagneta, kakvi se upotrebljavaju u znanstvene svrhe, uzvojnica se sastoji od razmjerno malenog broja uzvoja šuplje bakrene cievi, kroz koju teče voda za hlađenje, uz veliku gustoću struje. Tim se umanjuje razsipanje magnetnih silnica.
 Sl. 7. Lončasti elektromagnet
Sl. 7. Lončasti elektromagnetZadatak je vrlo jakih elektromagneta drugčiji u tehnici nego u znanstvenim zavodima. Zato je i njihova izvedba različita, iako je u oba slučaja osnovna težnja približavanje zatvorenome magnetskom krugu. Od jakih elektromagneta traži se u tehnici velika nosivost (za dizala). Najrazšireniji oblik takva elektromagneta je t. zv. lončasti elektromagnet, koji su nekako u isto doba (oko 1850) opisali Romershausen, Guillemin i Fabre. Taj je oblik shematski prikazan u sl. 7 (presjek). Nadesno crtkana ploha je željezna jezgra, dvostruko crtkana ploha je uzvojnica; žice do nje vode kroz jednu rupu u jezgri. Donji rub jezgre je točno ravno izbrušen, tako da na nj točno prianja jaka kotva (donja, nalievo crtkana ploha) od iste vrsti želieza, kojoj je gornji rub također točno ravno izbrušen. Jezgra i kotva imaju kvake za vješanje. Jezgra se magnetizira tako, da njezin srednji dio ima jedan, a vanjski zvonoliki obvoj drugi polaritet. Kad je kotva prionula uz jezgru, može se reći, da sve silnice prolaze kroz željezo; tragova razsipanja ima samo na neznatnom zračnom sloju između kotve i jezgre. Odatle dolazi neka potežkoća u rukovanju, jer zbog gotovo podpuno zatvorenog magnetskog kruga ostaje jak ostatni magnetizam, kad struju u uzvojnici prekinemo. U dizalima za željezne terete upotrebljavaju i t. zv. otvoreni oblik lončastog elektromagneta, gdje ulogu kotve ima željezni teret, koji se nahvata između srednjeg diela jezgre i zvonolikog obvoja (sl. 8).
 Sl. 8.
Sl. 8.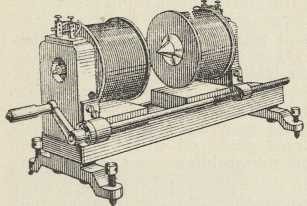 Sl. 9. Elektromagnet
Sl. 9. Elektromagnet
Ruhmkorffova oblika Sl. 10. Du Boisov poluprstenasti
Sl. 10. Du Boisov poluprstenasti
elektromagnetZadatak elektromagneta u znanstvene svrhe je stvaranje jakih magnetskih polja u više ili manje ograničenom prostoru. Izrežemo li iz prstenastog elektromagneta jedan kratak cilindrički komad jezgre, tako da prsten ostane nepodpun, na tome mjestu imamo jako magnetsko polje, koje je oko sredine izrezka homogeno. Na taj način prstenasti elektromagnet je uzorom i za elektromagnet u znanstvene svrhe. Elektromagneti, koji daju magnetska polja do najviše 30 kiloersteda u prostoru oko 1 cm3, pripadaju ili starijem Ruhmkorffovu obliku (sl. 9) ili novijim oblicima od Du Boisa (1894), kod kojih je razsipanje silnica manje; to su Du Boisov prstenasti elektromagnet i razšireniji poluprstenasti elektromagnet (sl. 10). Jako magnetsko polje dobiva se u zračnom prostoru među krajevima jezgre, t. zv. polovima. Među paralelnim čeonim plohama polnih nastavaka s promjerom plohe do kojih 5 cm mogu se dobiti kod malenog razmaka približno homogena polja jakosti 10 do 15 kiloersteda. Jača polja, znatno nehomogena, dobivaju se među nastavcima oblikom prikraćenog čunja. Po najnovijim iztraživanjima kut među izvodnicama čunja treba iznositi 120°; većina velikih elektromagneta ima stariju Stefanovu vriednost tog kuta 109,5°. Veliki Du Boisov elektromagnet daje u prostoru 0,32π 0,1 cm3 među čeonim plohama jakost polja 45 kiloersteda uz potrošak snage struje 2 kW.
 Sl. 11. Veliki elektromagnet K. Onnesa
Sl. 11. Veliki elektromagnet K. OnnesaTo je odprilike gornja granica za elektromagnete, kojima se još dade lako rukovati. S povećanjem jakosti polja nerazmjerno brzo rastu i veličina elektromagneta te snaga potrebnog izvora energije i potežkoće u rukovanju. U sl. 11 prikazan je veliki elektromagnet Kammerlingh Onnesa izrađen od tvrdke Siemens i Halske. U najnovijim najjačim elektromagnetima i u elektromagnetima ciklotrona (v.) oponašan je lončasti elektromagnet. Jaram elektromagneta čini zatvoreni željezni okvir, iz kojega prema unutra izlaze polne jezgre s uzvojnicama za magnetiziranje. Na taj način magnetski tok čini dvostruki zatvoreni krug, prekinut samo među čeonim plohama čunjastih polnih nastavaka; tu je jako magnetsko polje. Takav oblik ima dosada najjači, a i najsavršeniji elektromagnet na svietu, onaj sveučilišta u Uppsali (Švedska); stavljen je u porabu 1934. Ukupna mu je težina 37 tona. Uzvojnice su mu kratke, plosnate, s velikom gustoćom struje, uz hlađenje vodom. Uz potrošak snage od 98 kilovata on daje među ravnim čeonim plohama čunjastih polnih nastavaka u prostoru 0,522π • 0,6 cm2 jakost polja 62 kiloersteda, a u prostoru 22π • 2,3 cm3 jakost polja 47 kiloersteda. U poredbi s velikim elektromagnetom Francuzke akademije, koji se nalazi u mjestu Bellevue kod Pariza, a teži 120 tona, uppsalski elektromagnet uz jednak potrošak električke snage daje jednake jakosti polja na odprilike 1,4 puta većem prostoru r2π • d (r = polumjer čeone plohe, d = razmak među čeonim plohama).
Veliki tehnički zahtjevi nastaju, kad se proizvode trajna vrlo prostrana i jaka magnetska polja, koja su homogena u većem svom dielu, kako je to kod uređaja za savijanje staza korpuskularnih zraka u Wilsonovoj komori (v.), a osobito kod ciklotrona (v.). Rutherford je za iztraživanje alfazraka upotrebljavao elektromagnet težine 2,25 tona, koji uz potrošak snage 2,2 kilovata daje trajno magnetsko polje jakosti 18 kiloersteda, homogeno na 0,l%, u prstenastom prostoru sa srednjim polumjerom 40 cm, širine 5 cm, dubine 1 cm. Jedan njegov elektromagnet za iztraživanje savijanja staza korpuskula iz kozmičkih zraka daje uz potrošak 25 kilovata magnetsko polje jakosti 12,5 kiloersteda u prostoru 12,52π • cm3 među čeonim plohama. U najnovije vrieme su u svrhu iztraživanja tragova korpuskula iz kozmičkih zraka upotrebljavali i magnetsko polje uzvojnica bez željeza uz vrlo velike jakosti struje. Tako je Cotton (1938) dobivao u prostoru 75×20×4 cm3 polje jakosti 4 kiloersteda kod jakosti struje u uzvojnici 30 hiljada ampera (struja iz Poirsonova unipolarnog dinama).
Vrlo kratkotrajna, a izvanredno jaka magnetska polja u prostorima reda veličine 1 cm3 pomoću uzvojnica bez željeza proizvodi su Walla i Kapitza. Wall (1924) je u tu svrhu upotrebljavao izbijanje baterije kondenzatora velikog kapaciteta nabijene na visoku napetost; dobivao je magnetska polja jakosti do 1400 kiloersteda u trajanju 0,001 sec. Kapitza je najprije (1924) radio s časovitim jakim strujama, dobivenim kratkim spojem posebno u tu svrhu sagrađenih akumulatora, a kasnije (1927) kratkim spajanjem jakog izmjeničnog generatora kroz jednu poluperiodu. Dobivao je na prostoru 2 cm3 magnetska polja jakosti 320 kiloersteda kroz vrieme od oko 0,01 sec.
LIT.: (novija): A. Cotton, Comptes rendus 187 (1928); Cotton-Dupouy, C. R. 190 (1930); Cotton-Belling, C. R. 198 (1934); Cotton, Nuovo Cimento 15 (1938); L. Dreyfus, Arch. f. Elektrot. 29 (1931); Dreyfus, Elektrot. u. Maschinenbau 53 (1935); T. F. Wall, Nature 113 (1924) i 114 (1924); P. Kapitza, Proceedings of Royal Society 105 (1924) i 145(1927).M. K.
Elektromagnetska indukcija → Indukcija.
Elektromagnetski valovi. Nauka o elektromagnetskim ili električkim valovima nastala je s Maxwellovom teorijom elektriciteta, napose s njegovom elektromagnetskom teorijom svjetlosti (1873). Iz ove teorije izlazi, da se električki titraji duž ravne žice, kroz uzduh, prazan prostor (eter) ili drugi izolator šire kao elektromagnetski valovi brzinom, koja je jednaka brzini svjetlosti u tim sredstvima. Po toj su teoriji i valovi svjetlosti vrlo kratki elektromagnetski valovi. Za širenje električkih titraja i širenje svjetlosti uzima Maxwell isto sredstvo, eter, i kaže: ne bi se dalo filozofski opravdati, kad bi za tumačenje novih pojava svakiput izpunjavali prostor drugim sredstvom.
Poznatim Hertzovim pokusima (→ električki titraji 2) bio je cilj, da se eksperimentalno izpita vriednost Maxwellove teorije. Hertz je radio s progresivnim i stojnim valovima na žici i s valovima u slobodnom prostoru.
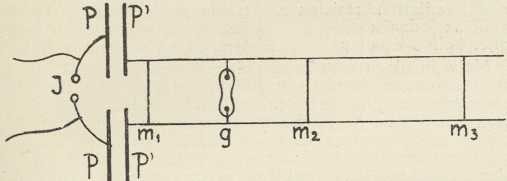 Sl. 1. Lecherov spoj
Sl. 1. Lecherov spoj1. Elektromagnetski valovi na žici. Za proučavanje ovih valova dao je E. Lecher eksperimentalni uređaj nacrtan u sl. 1. Imamo ovdje Hertzov oscilator sastavljen od iskrišta I i kovniih ploča PP. Njima su nasuprot ploče P'P' s uzporednim Lecherovim žicama, koje se na zgodnim mjestima kratko spajaju »mostovima«, t. j. žicama m1, m2, m3... Prvi most m1 stavlja se na mjesto, da s njim omeđen krug titranja s pločama P'P' bude u resonanciji s primarnim krugom. Most m2 dolazi na takvo mjesto, da Geisslerova cjevčica (g), koja se nalazi u sredini razmaka m1, m2, najjače svietli. Mjesta m1, m2 jesu čvorovi napetosti (čvorovi električke sile) i ujedno trbusi struje (trbusi magnetske sile). Na srednjem mjestu (g) nalazi se trbuh napetosti, odnosno čvor struje. Na tom su mjestu oscilacije napetosti među žicama najjače, dok je struja u žicama trajno jednaka ništici. Duž jednakog sliedećeg razmaka m2 m3 = m1 m2 = λ/2, gdje je λ valna dužina, stanje se ponavlja. Na žicama razmješteni čvorovi i trbusi napetosti (trbusi i čvorovi struje) čine sustav stojnih električkih valova. Između napetosti i struje postoji razlika faze π/2, t. j. kad struje u žicama dosegnu najveću vriednost, napetost je jednaka ništici.
Stojni električki valovi mogu nastati također duž žice jedne uzvojnice. Takav slučaj, uz induktivnu vezu krugova titranja, imamo i kod Teslina transformatora (→ električki titraji 3).
Za širenje električkih valova na žici vriedi obća formula c = fλ. Pomoću valne dužine λ, koju Lecherov pokus neposredno daje, i pomoću frekvencije f, izračunane po Thomsonovoj formuli (→ električki titraji 8), može se odrediti brzina c. Trowbridge i Duane su odredili frekvenciju oscilatora u Lecherovu spoju eksperimentalno na način Feddersenov razstavljanjem iskre u zrcalu, koje rotira (1895). Kod tih pokusa bilo je f = 5,29 • 106/sek, λ = 56,8 m. Izlazi c = fλ = 3,005 • 1010 cm/sek (= brzini svjetlosti u vakuumu). Ako se u formulu λ = c/f uvrsti frekvencija tehničke izmjenične struje 50/sek, izlazi λ = 6 000 km.
Na brzinu širenja električkih valova ne utječe tvar ni debljina žice, ali utječe okolno dielektričko sredstvo. Ako se žice nalaze u sredstvu s dielektričkom konstantom ε, za brzinu širenja valova vriedi Maxwellova formula v = c/√ε. Označimo li sa L samoindukciju za 1 cm Lecherovih žica, sa C odgovarajući kapacitet, izlazi za vrieme titraja τ = λ√LC, a za brzinu valova izraz v = 1/√LC.
Teoriju elektromagnetskih valova, koji se uzbuđuju po dugim brzojavnim ili telefonskim vodovima, obradili su Heaviside i K. W. Wagner. Stavlja li se na početak voda izmjenična napetost, uzbuđeni se val očituje kao valna napetost V i kao valna struja I. K. W. Wagner uvodi ovdje pojam valnog odpora Z = V/I. (Wellenwiderstand, résistance de l’onde). Ta je veličina nezavisna o mjestu i ima istu dimenziju kao elek. odpor. Za nju vriedi formula Z = √L/C. Kod nezgodne vriednosti valnog odpora mogu nastati smetnje u telefonskom saobraćaju.
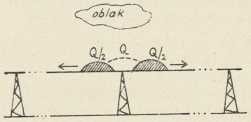 Sl. 2. Postanak putnih valova na dalekovodu
Sl. 2. Postanak putnih valova na dalekovodu
za jaku strujuU tehnici jake struje mnogo su iztraživali elektromagnetske valove na žici, koji se zovu putni valovi (ondes mobiles, Wanderwellen). Oni se očituju u časovitom povišenju pogonske napetosti u dalekovodu za jaku struju. Nastaju, kad se na dugi vod priključuju električki strojevi (generatori, transformatori). Osobite jake putne valove u slobodnim dalekovodima izazivaju bliza izbijanja atmosfere (olujni valovi, Gewitterwellen). Njihov postanak prikazuje sl. 2, u kojoj je sa Q označen vezani električki naboj, koji influencijom izvodi oblak. Taj je naboj nepomičan, dok se ne mienja električko polje između oblaka i zemaljskog tla. Bližim udarcem munje izjednačuju se naboji oblaka i tla. Naboj Q tim se oslobađa i ciepa u dva diela, koji putuju po dalekovodu protivnim smjerovima brzinom c = 3 • 1010 cm/sek. Višestrukom refleksijom ovih naboja na krajevima razvijaju se putni valovi, ako dalekovod ima dovoljno veliku dužinu. Frekvencija ovih valova na dalekovodu dužine l, kojem su krajevi izolirani, računa se po formuli f = c/2l. Za l = λ/2 = 150 km izlazi f = 1000 titraja u sek. Drugčije su prilike, ako radimo s dvostrukim dalekovodom, kojem su oba vodiča spojena na jednom kraju. Na tom se kraju valne struje zbrajaju, dok je radi refleksije valna napetost trajno jednaka ništici.
Primjer: Valna napetost V = 50.000 volta; valni odpor Z = 500 oma; valna struja I = 100 amp.; snaga N = 5000 kW.
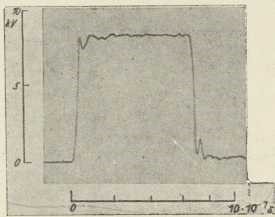 Sl. 3. Oscilogram putnog vala
Sl. 3. Oscilogram putnog vala Sl. 4. Hertzov štaposcilator
Sl. 4. Hertzov štaposcilator
(dipol)Premda ovakvi pojavi traju vrlo kratko vrieme (na pr. samo 10-5 sek, ako je λ = 3 km), mogu načiniti velike štete u priključenim strojevima. Našlo se međutim, da je opasnost to manja, što je veća radna napetost stroja. Utvrđeno je na pr., da kod uređaja, koji radi sa 6000 volta, lako dolazi do probijanja izolacije među početnim zavojima transformatora, koji je na vod priključen, dok su uređaji za vrlo visoke napetosti (220.000 volta) neosjetljivi prema ovakvim zalutalim putnim valovima. Da se zaprieči razorno njihovo djelovanje, načinjene su različne zaštitne sprave s odporima, ugušivačima, kondenzatorima i iskrištima. U novije vrieme izpituju ove pojave katodnim oscilografom (Gábor, Rogowski i dr). Sl. 3 pokazuje oscilogram putnog vala, koji se dobio kod stavljanja 100 m dugog voda na napetost 5.000 volta. Podvostručenje napetosti nastalo je refleksijom naboja na slobodnom kraju voda. Strmi početni dio oscilograma (čelo putnog vala) dug je 3 m i traje oko 10-8 sek. 2. Slobodni elektromagnetski valovi. Od električke iskre u sredini »otvorenog oscilatora« (oscilatora dipola sl. 4) šire se električki valovi na sve strane. Brzina širenja ista je kao kod valova duž žice. Energija, koja elektromagnetskim zračenjem izlazi u prostor, raste s 4. potencijom frekvencije. Kod nizkih frekvencija ta je energija neznatna, i to je razlog, da se tek kod vrlo visokih frekvencija (108 do 109 u sek), s kakvim je Hertz radio, mogla opažati. U središtu je oscilatora trbuh titranja, na krajevima su čvorovi titranja. Približno je λ = 2l, f = 3.1010/2l, gdje je l dužina dipola, f frekvencija, λ valna dužina. Polazeći od Maxwellovih jednačbi Hertz je računom i konstrukcijom odredio »faze« električkog polja u okolini dipola. Početno stanje toga polja pokazuje sl. 5a—e.
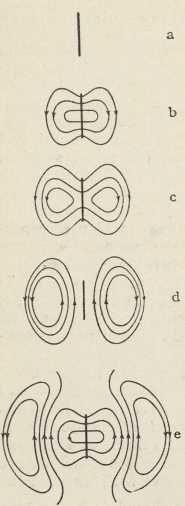 Sl. 5. Momentana stanja električkog polja
Sl. 5. Momentana stanja električkog polja
oscilatora-dipolaMagnetske silnice jesu koncentrične kružnice u ravninama okomitim na dipol. Gustoća i smjer magnetskih silnica mienjaju se periodski. Zajedno s električkim poljem širi se i magnetsko.
Kod teoretskih razmatranja dieli se prostor oko dipola u blizko i daleko područje. Daleko područje počinje u daljini r ≈ 4π i zove se područje ili polje zračenja. Iz Hertzove teorije sliedi, da se u blizkom području jakost električkog polja (E) u radialnom smjeru mienja razmjerno s 1/r3, a jakost magnetskog polja (H) sa 1/r2. Razlika faze između oba polja iznosi π/2. U dalekom području veličine E i H opadaju sa 1/r. Među njima nema fazne razlike.
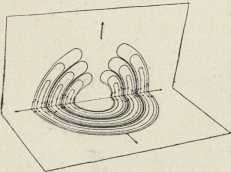 Sl. 6. Presjeci kroz
Sl. 6. Presjeci kroz
prostorno polje zračenjaSl. 6 pokazuje dva okomita presjeka kroz daleko elektromagnetsko polje dipola. U vertikalnom presjeku nacrtane su električke silnice, u horizontalnom magnetske. Sliku bi trebalo prostorno izpuniti i zamisliti, da se električko i magnetsko polje razteže brzinom svjetlosti kao mjehur od sapunice.
Jednostavan slučaj širenja elektromagnetskog vala predočuje sl. 7. Smjer širenja x nalazi se u ravnini simetrije (ekvatorialnoj ravnini) dipola AB. Električki i magnetski val su polarizirani. Vektori E i H titraju u stalnim ravninama, koje zatvaraju kut 90°.
Za maksimalne jakosti električkog i magnetskog polja u daljinu r vriede u ovom slučaju formule
\(\qquad\qquad\displaystyle E=\cfrac{60\;\pi\;I_0\;l}{r\;\lambda}\;\)
volta na cm;
\(\qquad\qquad\displaystyle H=\cfrac{5\;I_0\;l}{r\;\lambda}\;\)
amperzavoja na cm,
u kojima je maksimalna struja u dipolu, l dužina dipola. Veličine l, r, λ računaju se u cm, I0 u amperima.
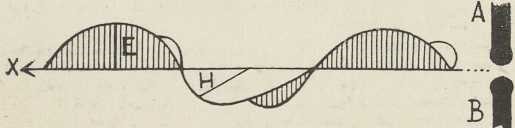 Sl. 7. Elektromagnetsko polje za smjer širenja
Sl. 7. Elektromagnetsko polje za smjer širenja
okomit na osi dipolaZamršenije su prilike, ako se promatra širenje vala u kosim smjerovima. U takvim slučajevima nisu ni električko ni magnetsko polje okomiti na smjeru širenja, kako to sliedi iz sl. 6. U smjeru osi dipola je E = H = 0.
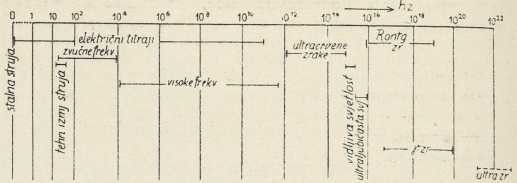 Sl. 8. Elektromagnetski spektar
Sl. 8. Elektromagnetski spektarStruja elektromagnetske energije kroz 1 cm2 u 1 sek (tok zračenja) definira se izrazom S = EH sin φ, gdje je φ kut među vektorima E i H. Mjerimo li E sa volt/cm, H sa amperzavoj na cm, izlazi S u jedinicama vat/cm2.
Za snagu zračenja (puissance rayonnée, power radiated, Strahlungsverlust), t. j. za energiju, koja zračenjem izlazi u okolni prostor u 1 sek, vriedi izraz
\(\qquad\qquad\displaystyle N=40\;\pi^2\;\cfrac{l^2}{\lambda^2}\;I_0^2=80\;\pi^2\;\cfrac{l^2}{\lambda^2}\;I^2,\)
u kojem I znači efektivnu struju u dipolu. Veličina
\(\qquad\qquad\displaystyle R=80\;\pi^2\;\cfrac{l^2}{\lambda^2}\)
zove se odpor zračenja (radiance, résistance de rayonnement, radiation resistance, Strahlungswiderstand). Ta je veličina jednaka odporu, u kojem bi se trošilo toliko energije, koliko dipol gubi zračenjem. Mjeri se omima (Ω).
Najveću ulogu u radiotehnici imaju poluslobodni valovi. Ako sredinom vertikalnog dipola položimo vodljivu horizontalnu ravninu, ne će to utjecati na oblik silnica ni na struju u dipolu. M. Abraham i Blondel pokazali su (1901), da za dipol izvedena teorija vriedi i u ovakvom slučaju, gdje za gornji dio dipola uzimamo vertikalnu antenu, a za donji dio savršeno vodljivu ravnu »zemlju«. Za snagu zračenja i za odpor zračenja izlaze formule
\(\qquad\qquad\displaystyle N=160\;\pi^2\;\cfrac{h^2}{\lambda^2}\;I^2,\quad R=160\;\pi^2\;\cfrac{h^2}{\lambda^2},\)
u kojima h znači efektivnu visinu antene, l efektivnu struju.
Ako je razmještaj struje duž antene sinusoidalan, efektivna visina antene s dužinom H dana je izrazom
\(\qquad\qquad\displaystyle h=\int_0^H{\rm sin}\;\cfrac{2\;\pi\;x}\lambda\;d\,x.\)
Primjeri: a) Za unifilarnu antenu, koja titra s četvrtinom valne dužine (H = λ/4), izlazi
\(\qquad\qquad\displaystyle h=\cfrac{2\;H}\pi=\cfrac\lambda{2\;\pi},\quad R=40\,\Omega.\)
b) Podatci za radio-postaju Croix d’Hins — Bordeaux: cieli odpor antene R' = 0,8Ω;
efektivna struja u podnožju antene I = 480 amp.;
antenska snaga R'I2 = 0,8∙4802/103 = 184 kilovata;
efektivna visina antene h = 170 m;
valna dužina λ = 18 900 m;
odpor zračenja R = 160π2h2/λ2 = 0,12 Ω;
stupanj djelovanja η = RI2/R'I2 = 0,15.
Prema tome od 184 kilovata u anteni izlazi zračenjem u prostor samo 27,6 kilovata (15%). Kod rada s kratkim valovima stupanj je djelovanja mnogo veći.
3. Elektromagnetski valovi obuhvaćaju veliko područje fizikalnih pojava, koji svi čine ukupni elektromagnetski spektar. Cielo to područje od 0 do 1023 titraja u sekundi (hertza, hz) predočeno je u sl. 8. S obzirom na frekvenciju svojstva i učinci su ovih valova vrlo različni. Područje od 0 do 1011 hz pripada valovima, koje proizvodimo električkim spravama. Tehnika jake struje radi sa 0 hz (stalna struja) i sa 15 do 60 hz (nizkofrekventna izmjenična struja). Električki titraji, izazvani čujnim zvučnim valovima, obuhvaćaju audiofrekvencije od 16 do 16.000 hz. Vidljivom spektru pripadaju frekvencije 3,8 • 1014 do 8,3 • 1014 hz. Najviše frekvencije pripadaju Röntgenovim i ultrazrakama.
Pregled elektromagnetskog spektra prema valnim dužinama daje sliedeća tablica:
| Vrst valova (zraka) |
λ (cm) |
| električki valovi |
2 • 106 – 8 • 10-3 |
| ultracrveni spektar |
3,4 • 10-2 — 7,8 • 10-5 |
| vidljivi spektar |
7,8 • 10-5 – 3,6 • 10-5 |
| ultraljubičasti spektar |
3,6 • 10-5 – 1,4 • 10-6 |
| Röntgenove zrake |
6,6 • 10-6 – 1,6 • 10-9 |
| najkraće γ-zrake |
0,5 • 10-10 |
| sekundarne ultrazrake |
~ 10-12 do 10-13 |
U tehnici visoke frekvencije razlikujemo duge, srednje, granične, kratke i ultrakratke valove. Dugim valovima, koji se upotrebljavaju najviše u radiotelegrafiji, pripadaju valne dužine λ > 2000 m. Za srednje je valove λ = 200 — 2 000 m, za granične λ = 100 — 200 m, za kratke λ = 10 — 100 m. Ultrakratki valovi λ < 10 m služe u televiziji. Valovi λ < 1 m zovu se mikrovalovi, dm-, cm-, mm-valovi. Mjesto podataka o valnim dužinama pišu se u novije vrieme podatci frekvencije u kilociklima (kilohertzima, khz). Metodom električke iskre postignuti su najkraći električki valovi λ = 0,08 mm, koji sežu u ultracrveni spektar (Glagoleva Arkadieva, 1924). Zajedničko je svojstvo sviju elektromagnetskih valova, da se sastoje od električkog i magnetskog vala i da se kroz prazan prostor šire jednakom brzinom.
4. Metode dobivanja električkih valova → električki titraji 2, 3, 4, 5, 6.
5. Širenje električkih valova, s kojima se služi radiotehnika, vrlo je zamršen pojav. Glavni su utjecaji električka svojstva valova (valna dužina, prigušenje), vrieme (dan, noć, godišnje doba), oblik i svojstva zemaljske površine (kopno, more), prilike u atmosferi. Do nekog obćeg rješenja ovog pitanja nije nauka došla.
Sommerfeld u svojoj teoriji (1909) razlikuje prostorne valove i valove duž zemaljskog tla. Od antene odašiljača šire se prostorni valovi u kuglama. U većim daljinama njihovo električko polje opada sa 1/r, a energija sa 1/r2. Valovi duž tla prodiru djelomice u zemlju i mogu se izporediti s valovima na žici. Njihovo električko polje opada sa 1/ √r, a energija sa 1/r. U većim daljinama preteže energija valova duž tla. No radi absorpcije u zemlji u vrlo velikoj daljini mogu ipak doći do jačeg izražaja prostorni valovi. Obje su vrste valova u međusobnoj vezi. Nemoguće ih je razstaviti, kao što je nemoguće odieliti električko polje od magnetskog. Za efektivnu jakost električkog polja vriedi po Sommerfeldu formula
\(\qquad\qquad\displaystyle E=120\;\pi\;\cfrac{h\;I}{\lambda\;r}f(\varrho)=\cfrac{377\;h\;I}{\lambda\;r}f(\varrho)\qquad\qquad\)(1)
(h, λ, r kilometri, I amperi, E milivolti na metar, mV/m).
Faktor absorpcije ili Sommerfeldova funkcija f (ρ) zavisi o dielektričkoj konstanti i o električkoj vodljivosti tla. Poslužimo li se izrazom za snagu zračenja u kilovatima, dobivamo za jakost električkog polja jednostavniju formulu E = 300/r√Nf (ρ)(2)(r kilometri, N kilovati, E mV/m).
Formule (1) i (2) mogu se primieniti na srednje valove, ako daljina r iznosi nekoliko stotina km.
6. Širenje dugih valova na velike daljine, gdje dolazi u obzir i zakrivljenost Zemlje, iztraživali su Austin, Appleton, Zenneck, Kiebitz, Bäumler i dr. Služeći se velikim brojem empiričkih podataka izveo je Austin za efektivnu jakost električkog polja poluempiričku formulu (1926)
\(\qquad\qquad\displaystyle E=120\;\pi\;\cfrac{h\;I}{\lambda\;r}\sqrt{\cfrac\alpha{{\rm sin}\,\alpha}}\;e^{-0,0015\,r/\lambda^{0,6}}\)
(h, λ, r kilometra, I amp., EmV/m).
U ovoj je formuli α kut, pod kojim bi se iz središta Zemlje vidjela daljina r. Faktor absorpcije e-0,0015 r/λ0,6 izveden je za širenje valova λ = 500 do 25.000 m nad morskom površinom po danu (r > 1000 km). Za utjecaj zemaljske zakrivljenosti izveo je Kiebitz izraz α/sinα. Za širenje valova do mjesta antipoda ne može se upotrebiti ni Kiebitzova ni Austinova formula. Za takav slučaj izlazilo bi α/sinα = ∞, √α/sinα = ∞. Drugi iztraživači dobili su za faktor absorpcije izraze s različnim empiričkim konstantama.
Primjeri: 1. Odašiljač Croix d’Hins (Bordeaux): h = 0,17 km, λ = 18,9 km, I = 480 amp. Račun po Austinovoj formuli daje za r = 6.000 km (= daljina Bordeaux—New-York) E ~ 0,06 mV/m.
2. Iz podataka za zagrebački odašiljač h ~ H = 50 m, λ = 476,9 m, I = 25 amp., za daljinu r = 1000 km izlazi po Austinovoj formuli E ~ 0,1 mV/m Za primanje detektorom treba E ~ 3 mV/m.
Da je Zemlja savršena kugla, bila bi prema teoriji jakost električkog polja na mjestu antipoda ista kao u blizini odašiljača valova. No radi sploštenosti Zemlje nisu u takvom slučaju jednaki svi putovi valova. Zbog razlike u fazi, koja tim nastaje, mogu se na diametralnome mjestu Zemlje valovi oslabiti. Motrenja pokazuju, da je u području 100 km oko mjesta antipoda električko polje znatno pojačano.
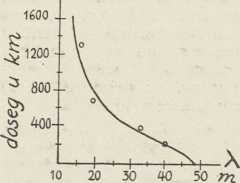 Sl. 9. Zavisnost dosega zone o valnoj dužini
Sl. 9. Zavisnost dosega zone o valnoj dužini7. S kratkim valovima postizava se brzojavna i telefonska veza na vrlo velike daljine, iako odašiljač radi s malenom snagom. Valovi, veći od 60 m, vladaju se uglavnom kao srednji i granični valovi. Noću sežu dalje nego danju. Kod još kraćih valova nastaju zamršenije i anomalne prilike. U razmjerno malenoj daljini od odašiljača počinje t. zv. mrtva zona ili zona šutnje (→ akustika 4), u kojoj je primanje nemoguće i uz pojačanu snagu odašiljača. U mnogo većoj udaljenosti prestaje mrtva zona. Jakost električkog polja se skokom uveća. Kažemo, da kratki valovi preskakuju mrtvu zonu. Pojav je to izrazitiji, što je val kraći. Vanjski polumjer mrtve zone zavisi o dužini vala, o dnevnom vremenu i godišnjoj dobi. Noću seže mrtva zona dalje nego danju, zimi dalje nego u ljetno doba. Zavisnost toga dosega o valnoj dužini pokazuje sl. 9. Već je starije izkustvo pokazalo, da na primanje valova mnogo utječe valna dužina, dnevno vrieme i godišnje doba. Razlikovali su noćne valove (25—40 m), dnevne (10—18 m) i prelazne valove (19—24 m). Dvie daleke brzojavne postaje mogu uzdržati trajnu međusobnu vezu, ako, prema dnevnom vremenu i godišnjoj dobi, zgodno odabiru valne dužine.
Za anomalno širenje kratkih valova prihvatili su sliedeće tumačenje: Valovi, koji sliede zemaljsku površinu, absorbiraju se već nakon razmjerno malenog puta. Prostorni pak valovi, nakon refleksije na visokim ioniziranim slojevima uzduha (Heavisideov i drugi slojevi), vraćaju se i dolaze na mjesta izvan mrtve zone.
8. Valovi, kraći od 10 m, šire se pravocrtno kao valovi svjetlosti. Zovu se radi toga kvazi-optički valovi. Držali su, da je zbog toga njihov doseg ograničen optičkim horizontom. Radi pojava ogiba mogu se ovi valovi primati u mnogo većim daljinama. Za jakost električkog polja unutar optičkog horizonta vriedi formula E = 9,5 √N/r
(N vati, r km, E volti/metar).
Mikrovalovi upotrebljavaju se u aeroplanskom saobraćaju i pomorstvu (signaliziranje, pokazivanje tečaja broda). Prema Marconijevim pokusima granični doseg valova λ = 57 cm iznosi 270 km, dok je optički doseg bio samo 116 km.
9. Pojav radiojeke. Time, što električki valovi različnim putovima stižu na mjesto primanja, može nastati pojav radiojeke. U tom slučaju točkasti Morseov znak primamo kao dva bliza znaka. Prvi znak daju valovi, koji se šire duž zemaljske površine, a drugi potječe od prostornih valova reflektiranih na ioniziranom visokom sloju atmosfere.
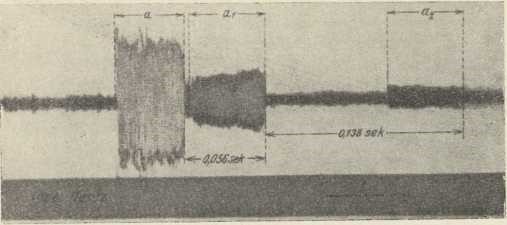 Sl. 10. Oscilogram znaka
Sl. 10. Oscilogram znaka
poslanog oko zemljeKod kratkih valova može nastati pojav radiojeke tako, da nakon prvog primanja valovi obiđu cielu Zemlju jedanput ili više puta. Sl. 10 pokazuje oscilogram takvog pojava. Odašiljač Buenos Aires; postaja za primanje Geltow; λ = 18,3 m; a = glavni primljeni znak; a1 = znak primljen iza prvog obilaženja Zemlje; a2 = znak primljen poslije drugog obilaženja Zemlje. Trajanje obhoda oko Zemlje 0,138 sek.
10. Detektori za električke valove → detektor → elektronska ciev.
LIT.: F. Bédeau, Cours élémentaire de Télégraphie et de Téléphonie sans fil, 1937; F. Vilbig, Lehrbuch der Hochfrequenztechnik, 1937; B. Beckmann, Die Ausbreitung der elektromagnetischen Wellen, 1940.D. P-ć.
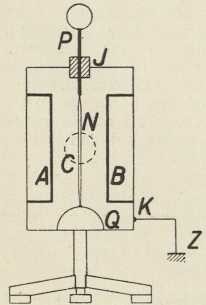 Sl. 1.
Sl. 1.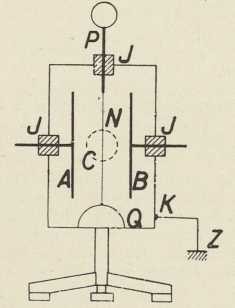 Sl. 2.
Sl. 2.Elektrometri, mjerne sprave s vrlo raznolično izvedenim pomičnim sustavima, koji se odklanjaju pod utjecajem elektrostatskih sila u slučaju postojanja električkoga napona između sustava i okolnog kovnog »kućišta«. Elektrometri su dakle u bitnosti bolji elektroskopi (v.) i po načelu djelovanja elektrostatski instrumenti, odakle i dolazi, da ih često, ako imaju skalu u jedinicama električkoga napona voltima, zovu i »elektrostatskim voltmetrima«. E. se prema galvanometričkim i drugim instrumentima, u praksi običnijima, odlikuju time, da kod mjerenja stalnih napona ne troše uobće nikakvu struju, dok kod priključka na izmjenične električke napone troše obično tek posve neznatnu i k tomu »praznu« ili »bezvatnu« električku struju. Dvie suvremene izvedbe e-a, od kojih je prva osjetljiva na umjereno nizke, a druga čak i neznatne električke napone, bile bi na pr. Wulfovi e.: dvonitni (sl. 1) i jednonitni (sl. 2). Dvonitni je u praksi vrlo običajan uzprkos umjerenoj osjetljivosti, jer je jednostavan u upotrebi. Prema sl. 1 lako je u njemu nazreti bitno usavršeni elektroskop sa zlatnim listićima (→ elektroskopi). I kod njega se naime vidi, izoliran jantarom J od kućišta K, kovni provod u obliku štapića P s kuglicom na gornjem kraju; samo se mjesto zlatnih listića, slobodnih na donjem kraju, nadovezuju na P dvie izvanredno nježne vodljive niti N (na pr. tanahne kovne žice od samo 1 ili 2 tisućinke milimetra promjera), koje elastično zajedno drži nježni kremeni stremen Q (kremen također dobro izolira). Zbog jačega elektrostatskoga djelovanja postavljeni su s obje strane niti kovni štapići A i B u vodljivoj vezi s kućištem. Nabije li se sustav s nitima pozitivno ili negativno prema kućištu, niti N se do izvjestne mjere razmaknu, jer ih privlače štapići A i B, i popušta im elastično stremen Q. Dragocjeno je pritom, da se položaj ravnotežja kraj sićušne mase nitî N uzpostavi osobito brzo, na pr. u malom dielku sekunde, tako da je instrumentom moguće pratiti i brzo promjenljive pojave. Mikroskopom ili projekcionim uređajem, udešenim poprilici za vidno polje ograničeno crtkanom kružnicom C u sl. 1, može se povećanje razmaka niti prema neznatnom njihovu početnom razmaku u nenabijenom stanju lako pratiti, i na prikladnoj skali u velikom povećanju odčitavati (bilo u mikroskopu, bilo u projekciji na velikom zaslonu vidljivom istodobno brojnom slušateljstvu). Skala može odmah biti u voltima (na pr. s mjernim obsegom od nekoliko volta do nekoliko stotina volta). Kod jednonitnoga e-a izvedba je po sl. 2 izmienjena ne samo po tom, što instrument ima samo jednu nit N, nego i po tom, što su štapići A i B također poput provodnika P jantarima J izolirano uvedeni. Tako A i B mogu tvoriti samostalne elektrode, između kojih se može podržavati »pomoćni napon« baterije B0 galvanskih elemenata. Ako je sredina baterije B0 spojena s kućištem K i sa zemljom Z, jedna od ploča A i B bit će pozitivna, a druga isto toliko negativna prema kućištu i zemlji, pa ako se pomoćni napon uzme dovoljno visok i recimo takva predznaka, da A bude pozitivno i B negativno, doći će i kod neznatno prema kućištu pozitivne električke niti N istodobno do jakoga odbijanja između N i jako pozitivne elektrode A i jakoga privlačenja između N i jako negativne elektrode B, te prema tomu do odklona niti N prema B (uz negativni naboj niti N ova bi se odklonila prema A). Upotrebom pomoćnog napona osjetljivost se instrumenta dakle znatno poveća, pa jednonitni e. reagiraju već na pr. na stotinke volta, i njihova će upotreba, uzprkos komplikacijama s izvorom pomoćnog napona, biti na mjestu, gdje se traže ekstremne osjetljivosti. Od starijih e-a još se i danas mnogo spominje naročito Kelvinov (Thomsonov) kvadrantni e-ar. Tehnički zanimljive su izvedbe elektrostatskih sprava, prikladne za mjerenja vrlo visokih napona (mnogo »kilovolta«); ovi se elektrostatskim visokonaponskim voltmetrima lakše neposredno mjere nego na pr. galvanometričkim voltmetrima posredno uz pomoć smanjenja napona mjernim transformatorima. E. nisu samu neobhodno potrebni za nastavne svrhe, nego i za vrlo važna naučna izpitivanja, na pr. iztraživanja radioaktivnosti, ionizacije zraka i t. d. Neke specialno osjetljive konstrukcije e-a kadre su mjeriti čak struje na pr. od samo 100 ili 1000 elektrona sekundno (600 elektrona sekundno odgovaralo bi struji od kojih 10-16 ampera!).J. L.
Elektromotorna sila shvaća se kao »skup sila«, koje razstavljaju protivne električke naboje, kao »uzrok« gibanja elektriciteta u vodiču, odnosno kao »uzrok«, koji u vodiču uzdržava potencialnu razliku (H. A. Lorentz). U vezi s izrazom e. s. dolazi izraz napetost među polovima njem. Klemmenspannung). Dok izvor ne daje električku struju, obje su veličine jednake. U zatvorenom krugu struje napetost je među polovima to manja od e-e s-e, što je veći gubitak napetosti u nutrašnjem odporu izvora. U elektrotehničkoj literaturi uvrštava se često e. s. u pojam električke napetosti. Hrvatske norme uvele su za e-u s-u oznaku E. Jedinica u praktičnom sustavu mjera za e-u s-u i za električku napetost jest volt (→ električke jedinice).D. P-ć.
Elektron (→ čestice elementarne).
Iztraživanjem katodnih zraka, betazraka te zraka, koje pri fotoelektričkom pojavu izlaze iz kovina, utvrdilo se, da su sve one u biti jednake: u njima se gibaju negativni elektricitet i masa nerazdružno povezani tako, da svaki gram nosi 1.76.108 kulon elektriciteta. Kako je taj naboj 1838 puta veći od onoga, što ga pri elektrolizi prenese 1 gram najlakšeg elementa, vodika, to je očit zaključak, da se u katodnim i srodnim zrakama mogu gibati samo krhotine atoma. Za te krhotine obćenito se ustalilo ime elektroni, pa se gore spomenute zrake zovu jednim imenom elektronske zrake. Pokusi s elektronskim zrakama učinili su vjerojatnom pomisao, da su elektroni sitna tjelešca. Ta je vjerojatnost znatno porasla, kad su u Wilsonovoj komori učinili vidljivima staze, kojima su pojedini elektroni prošli, i kada je Millikan pokazao, da postoji najmanji električki naboj.
Da predočbom o elektronu, kao tjelešcu s negativnim električkim nabojem, nije ovaj podpuno opisan, moglo se naslutiti već iz Bohrove nauke o atomima. De Broglie je iznio hipotezu, da su elektroni i valne prirode. Ona je našla eksperimentalnu potvrdu u difrakciji elektronskih zraka, pojavu značajnu za valove. »Valni paket« (v. 11) pokušaj je zornog spoja obiju predočbi o elektronu.
Novija kvantna nauka načelno se odriče zorne predočbe o elektronu pa postavlja matematičku shemu, kojom obrađuje elektron. Iz te sheme izlazi, kada se pri opisivanju pojava možemo služiti česticom, a kada valom kao slikom o elektronu.
1. ELEKTRONSKE ZRAKE ponajprije su opažene kao t. zv. katodne zrake (v.; Plücker, 1858). Hittorf je našao (1869), da se one šire pravocrtno, i da ih magnetsko polje može svinuti, dok je Goldstein odkrio (1876) odklon u električkom polju. Crookes (→ Crookes, Crookesove cievi) izveo je s katodnim zrakama pokuse, koji su učinili jak dojam na njegove suvremenike, i iznio je misao, da su one tvarne prirode. Perrin je jasno utvrdio (1895), da su one struja negativnog elektriciteta (→ Perrinova ciev), na što je upućivao i smjer odklona u magnetskom i električkom polju.
Lenard je pokazao (1899), da pri Hallwachsovu pojavu (→ fotoelektricitet) izlaze iz kovina, obasjanih ultravioletnom svjetlošću, elektronske zrake. Približno se u isto vrieme ustanovilo, da su i betazrake (v.) elektronske.
2. ODKLON ELEKTRONSKIH ZRAKA U ELEKTRIČKOM I MAGNETSKOM POLJU može poslužiti, da se izmjeri brzina v, te omjer e/m naboja e i mase m elektrona (J. J. Thomson, 1897).
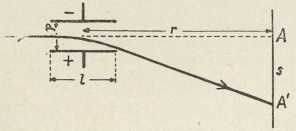 Sl. 1.
Sl. 1.Uzki svežanj elektronskih zraka upravi se između ploča ravnog kondenzatora, kojemu su ploče uzporedne s prvotnim pravcem svežnja (sl. 1). Ako među pločama nema električkog napona, svežanj ostaje pravocrtan i zgađa u točki A zastor, koji pod udarcima elektrona svietli (fluorescentni zastor). Kad se uzpostavi napon U, onda se u čitavom prostoru među pločama pobudi
električko polje jakosti E = U : d (d je razmak među pločama), pa na svaki elektron djeluje sila F = eE, koja ga vuče prema pozitivno električkoj ploči. Elektron se dakle u tom prostoru giba poput vodoravno bačenog kamena u polju zemljine teže, t. j. po paraboli. Zato sada zgodi zastor u točki A', koja je u daljini s od točke A. Ako je l duljina kondenzatora, dakle i prostora, u kojem vlada električko polje, a r razmak između sredine kondenzatora i zastora, to onda valja:
v2:e/m = Erl/s. (1)
Pobudi li se na jednom dielu puta elektronskih zraka magnetsko polje okomito na smjer svežnja, tad djeluje na svaki elektron sila F = evB, gdje B znači magnetsku indukciju u pobuđenom polju. Smjer te sile je okomit i na brzinu v i na smjer magnetskog polja (t. j. na smjer od B). Ako je l′ širina polja (sl. 2), r′ razmak između sredine polja i zastora, s' opaženi uklon, tad u ovom slučaju valja:
v: e/m =B r′l′/s′. (2)
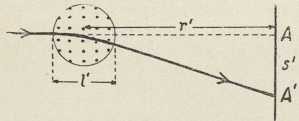 Sl. 2.
Sl. 2.U sl. 2 treba zamisliti, da je magnetsko polje nastalo tako, da se pred ravninom crtnje nalazio sjeverni magnetski pol.
U jednačbama (1) i (2) mogu se sve veličine na desnoj strani izmjeriti i time odrediti v odn. e/m. Nalazi se, da se elektroni gibaju brzinama od nekoliko tisuća km/sek pa sve do blizu brzine c svjetlosti u praznome prostoru; tako na pr. v u betazrakama RaC iznosi i 99% od c. Ako je v maleno prema c, tad je omjer e/m stalan (unutar granica pogrješke mjerenja) i iznosi l∙758.108kulon/gram=5∙270.1017 elst cgs/gram, međutim, kad se v približava brzini c, biva on sve manji i manji (Kaufmann, 1901), pa na pr. za spomenute elektrone iz RaC iznosi tek ⅐ navedene vriednosti. Budući da naboj e ne zavisi o brzini, to sliedi, da je masa ovih elektrona 7 puta veća od mase m0 sporih elektrona. Ovo je u skladu s izrazom, što ga daje teorija relativnosti za ovisnost mase nekog tiela o brzini:
\(\qquad\qquad\displaystyle m=m_0\,{\it :}\,\sqrt{1-v^2/c^2}.\)
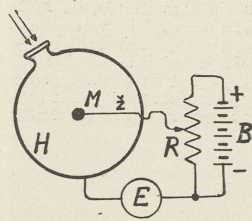 Sl. 3.
Sl. 3.Pri iztraživanju brzina elektrona u fotoelektričkom pojavu upotrebio je Lenard (1902) metodu »protivnog polja«. — U središtu šuplje vodljive kugle H (sl. 3), iz koje je odstranjen uzduh, nalazi se kovina M, koja se obasja svjetlošću kroz maleni prozor od kremenova stakla. Tad izlieću iz M elektroni, koje pohvata kugla H i vraća ih kroz vrlo osjetljiv galvanometar E, odpornik R i žicu ž kovini M. E pokazuje u tom slučaju električku struju. Ako se pomoću baterije B i odpornika R dade kovini M pozitivni, a kugli H negativni naboj, tad u kugli vlada električko polje, koje vuče izbačene elektrone natrag prema M. Ako je električki napon U između M i H baš tolik, da nijedan elektron ne stigne do kugle H, t. j. da kroz E ne teče električka struja, tad je kinetička energija, a time i brzina v najbržih elektrona određena izrazom eU = (m— m0)c2 ≈ m0v2/2, gdje je m masa tih elektrona (→ elektronvolt).
U tablici su u prvi stupac uneseni naponi U, koji bi po Lenardovoj metodi »protivnog polja« baš mogli zaustaviti elektrone, koji se gibaju brzinama v unesenim u drugi stupac. Brojevi u trećem stupcu kažu, koliko je puta pripadna masa m elektrona veća od m0.
| Napon U volt |
Brzina v km/sek |
m/m0 |
| 1 |
595 |
1∙00 |
| 100 |
5 950 |
1∙00 |
| 103 |
1∙87.104 |
1∙003 |
| 104 |
5∙85.104 |
1∙02 |
| 105 |
1∙65.105 |
1∙2 |
| 106 |
2∙83.105 |
3∙2 |
| 3∙1.106 |
2∙97.105 |
7∙1 |
3. NABOJ ELEKTRONA e (odn. masa m) ne može se odrediti iz odklona elektronskih zraka u električkom i magnetskom polju. Za to su potrebne druge metode. Pojavi elektrolize (v.) upućuju na postojanje najmanje množine električkog naboja. No taj naboj dobivamo iz naboja golemog broja čestica, koje u elektrolizi sudjeluju, pa je bila opravdana sumnja, nije li on tek neka srednja vriednost.
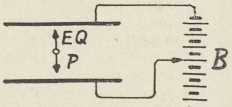 Sl. 4.
Sl. 4.Millikan je (1911 i dalje) »metodom kapljice« odredio najmanji električki naboj, koji se može jednom tielu dati odn. oduzeti. — Sitna kapljica ulja pada kroz mirni uzduh stalnom brzinom, jer njezinoj težini drži ravnotežu sila, koja nastaje od trenja s uzduhom. Pri tome ona poprimi oblik kugle radi površinske napetosti. Iz brzine padanja, specifične težine ulja te koeficienta viskoznosti i specifične težine uzduha mogao je Millikan odrediti polumjer kapljice (nekoliko tisućina mm), dakle i njezinu težinu. Već kod razpršavanja ulja u kapljice ove se redovito elektriziraju. No Millikan je mogao naboj kapljice promieniti tako, da je rentgenskim zrakama obasjao uzduh, kroz koji se kapljica giba. Ove zrake naime izbiju iz pojedinih molekula elektrone, i tako u uzduhu nastanu nosioci električkih naboja. Kad se takav nosilac pridruži kapljici, promieni ona skokom naboj. — Nosi li kapljica električki naboj Q, može se zgodnim homogenim električkim poljem (među pločama širokoga ravnog kondenzatora) vertikalnog smjera postići, da kapljica lebdi. Tad je sila EQ, kojom električko polje jakosti E djeluje na naboj Q, jednaka težini P kapljice (sl. 4); t. j. EQ = P. Kako su E i P poznati, to se odatle odredio naboj Q. Za taj je izašlo, bio on pozitivan ili negativan, da može imati samo neke odabrane vriednosti: 1e, 2e, 3e,..., gdje je e = l.60.10-19kulon = 4.80.10-10elst cgs. Ta se vriednost slaže s onom nađenom pri elektrolizi. Uzima se, da svaki elektron nosi naboj e. Masa m elektrona računa se iz omjera e/m. Izlazi m0 = 9∙10.10-28gram.
4. LORENTZOVA TEORIJA ELEKTRONA uzima, da dielovi atoma i molekula nose električke naboje. H. A. Lorentz ju je nadovezao (1895) na Maxwellovu teoriju (v.) elektromagnetskog polja, koja obrađuje tvarno sredstvo kao kontinuum, t. j. ne uzimajući u obzir njegovu strukturu. Već je Maxwell iztaknuo za svoj način razmatranja, da može biti valjan, ako su dužine elektromagnetskih valova vrlo velike prema veličini čestica, od kojih je tvar građena. — Lorentz nadalje predpostavlja, da je uviek mirni eter (v.) jedini nosilac elektromagnetskih polja i da izpunja neprekidno čitav svemir. Kroz eter se gibaju atomi pobuđujući svojim električkim nabojima zamršena elektromagnetska polja. Ta se polja dodaju k poljima izazvanim uzrocima izvan tiela. Zato se neko elektromagnetsko polje, na pr. žuta natrijeva svjetlost, drugčije razprostire Kroz prazni prostor, a drugčije kroz staklo. U posljednjem slučaju sudjeluju u pojavu i čestice, od kojih se sastoji staklo.
Uvodeći prikladne predočbe o građi tvari Lorentzova teorija je tumačila disperziju svjetlosti, dobru vodljivost kovina za električku struju i toplinu, magnetska svojstva tvari i još druge pojave.
Ampèreova hipoteza, da u pojedinim česticama magneta kruži elektricitet (→ Ampèreove struje), poprimila je u teoriji elektrona određeniji oblik u predpostavci, da se u atomima magneta gibaju elektroni po zatvorenim stazama. Uzme li se, da elektron izvodi to gibanje pod utjecajem sile, koja je upravljena prema čvrstom središtu, tad je njegova staza u ravnini, a veličina magnetskog momenta d, koji toj stazi pripada, razmjerna je s nabojem elektrona, površinom staze i frekvencijom obhoda. Kako elektron ima i masu, to je u ovom slučaju elektronov zakretni impulz p razmjeran s masom elektrona, površinom staze i frekvencijom obhoda. Izlazi, ako se služimo miešanim sustavom električkih jedinica, d = 1/2ce/m∙p. Svakom je magnetskom momentu pridružen posve određen mehanički zakretni impulz (magnetomehanički paralelizam). To vriedi i za čitav magnet, jer se njegov magnetski moment dobije geometrijskim zbrajanjem momenata njegovih djelića, a isto tako i zakretni impulz (→ Einstein-de Haasov pojav).
S poviestnog je gledišta značajno, da je Lorentzovo tumačenje t. zv. normalnog Zeemanova pojava (v.) također vodilo do elektrona, i to kao česticu, odgovornu za izsijavanje svjetlosti.
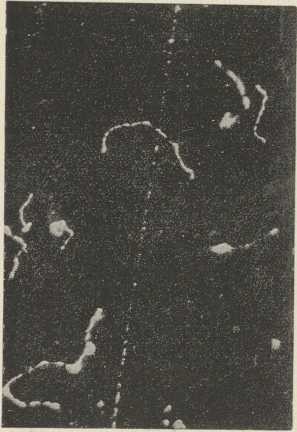 Sl. 5.
Sl. 5.5. RAZPRŠAVANJE I ABSORPCIJA ELEKTRONSKIH ZRAKA pripomogli su upoznavanju atoma. — Hertz je započeo (1892) izpitivanjem propustnosti tankih kovinskih listića za elektronske zrake. Ta je iztraživanja nastavio Lenard izvedavši elektronske zrake iz katodne cievi u uzduh kroz »Lenardov prozor« (1893). Lenard je našao, da se pri prolazu kroz tvar, na pr. uzduh, aluminij, i t. d., elektronske zrake razpršavaju i absorbiraju to manje, što su elektroni brži. Za pojedini elektron treba uzeti da je pritom prošao kroz mnogo tisuća atoma, prije nego što je znatnije skrenuo sa svojeg pravca ili u kojem atomu zapeo. Na osnovu toga i Ruthefordovih pokusa s alfazrakama (v.) nastala je predočba o atomu, poznata pod imenom Ruthefordov atom (1911; → atom 11).
Sl. 5 prikazuje staze elektrona u uzduhu postale vidljivima metodom Wilsonove komore (v.): ravni magleni trag potječe od jednog vrlo brzog elektrona, a svakojako svinuti od polaganijih izbačenih iz molekula uzduha fotoelektričkim pojavom.
O prolazu elektrona kroz tekućinu → Čerenkovljev pojav.
Za razpršavanje i absorpciju vrlo sporih e-a →Ramsauerov pojav.
Sraz fotona i elektrona → Comptonov pojav.
Također→ deltazrake.
6. BOHROVA TEORIJA uzima Ruthefordovu predočbu o atomu. N. Bohr se njome poslužio najprije pri tumačenju spektra vodikova atoma. U tom atomu kruži jedan elektron oko protona, koji ga privlači po Coulombovu zakonu. Po klasičnoj (Maxwell-Lorentzovoj) elektrodinamici morao bi takav elektron neprestano izsijavati elektromagnetske valove, a to bi išlo na račun njegove energije, pa bi u vrlo kratko vrieme stigao do samoga protona. Bohr predpostavlja, da postoji samo diskretan niz staza (kružnica), po kojima se može elektron gibati, i da elektron pritom ne izsijava valova. Te su kružnice određene Bohrovim kvantnim uvjetom, da zakretni impuls p elektronov može biti samo neki cjelobrojni mnogokratnik od h/2π, t. j.
p = n h/2π, n = 1, 2, 3,...,
gdje je h Planckov kvant djelovanja. Spektar vodika mogao je Bohr raztumačiti dodavši k tome još svoj »uvjet frekvencije«, u kojem po drugi put ulazi u ovu teoriju konstanta h. Po tom uvjetu atom izsijava svjetlost, kad elektron preskoči s jedne šire kružnice na užu.
Po magnetomehaničkom paralelizmu pripada najužoj kružnici (n = 1) magnetski moment
μ = eh/4πmc,
poznat pod imenom Bohrov magneton. Momenti širih staza su mnogokratnici ovoga.
A. Sommerfeld je profinio Bohrovu teoriju razmatrajući gibanje elektrona po elipsama i uzevši u obzir relativističku promjenu elektronove mase s brzinom. Time je tumačio finu strukturu vodikovih crta i našao novu vezu između naboja e elektrona i Planckova kvanta djelovanja h.
7. SPIN ELEKTRONOV je nova hipoteza o elektronu, do koje su dovela spektroskopska iztraživanja. — Već prije Bohrove teorije uspjelo je uglavnom razmrsiti spektre alkaličnih i zemnoalkaličnih kovina u serije. Pri tumačenju tih spektara Bohrovom teorijom ostalo je neriešeno pitanje višestrukih spektralnih crta, tako na pr. natrijeve dvostruke žute (5890 å, 5896 å). Isto tako nije objašnjen anomalni Zeemanov pojav. Sve te potežkoće rješava jednim udarcem hipoteza Goudsmita i Uhlenbecka (1925), da sam elektron ima magnetski moment jednak Bohrovu magnetonu i zakretni impulz, t. zv. spin, ½h/2π, dakle polovinu od onoga, koji bi mu po magnetomehaničkom paralelizmu pripadao.
8. PAULIJEVO NAČELO vriedi za razpored elektrona po raznim kvantnim stanjima u atomu, molekuli, dapače i u velikom komadu kovine. — Kvantno stanje jednog elektrona u bilo kojem atomu određeno je s četiri kvantna broja: n, l, ml, ms. Brojem n, t. zv. glavnim kvantnim brojem, određena je, uglavnom, energija elektrona, a brojem l, azimutalnim kvantnim brojem, koji može imati vriednosti 0, 1, 2,..., n — 1, oblik njegove staze. Svakom kvantnom broju l pripada 2l + 1 vriednost magnetskog kvantnog broja ml, a to su: —l, —(l—1),..., —1, 0, 1,... (l — 1), l. Konačno je ms spinov kvantni broj, koji može imati vriednosti -½, + ½. Paulijevo načelo kaže, da u jednom atomu ne mogu biti dva elektrona, kojima bi sva četiri kvantna broja bila jednaka, t. j. koji bi bili u istom kvantnom stanju. Prema tome, ako su dani brojevi n, l, ml, ms, tad može biti u atomu samo jedan elektron, kojemu ti brojevi pripadaju. U brojevima n, l, ml mogu se podudarati samo dva elektrona s obzirom na dvie vriednosti ms; dok se u brojevima n, l može podudarati 2(2l + 1) elektron, jer ml može poprimiti 2l + 1 vriednost. Konačno se u broju n može podudarati 2(2l + 1) = 2n2 elektrona; radi vriednosti, koje broj l može primiti. Tim je načelom raztumačen periodički sustav elemenata. U najnižem energetskom nivou, n = 1, t. zv. K-ljuski, mogu biti najviše 2 elektrona; u L-ljuski, n = 2, već 2 + 6 = 8 elektrona; u M-ljuski, n = 3, 2 + 6 + 10 = 18 elektrona, i t. d., a to su brojevi elemenata u periodama sustava elemenata.
Fermijeva statistika uzima Paulijevo načelo u svoje osnove.
Paulijevo načelo dade se donekle obrazložiti sa stajališta valne mehanike.
9. MATERIJSKI VALOVI jesu valovi, koje je L. de Broglie pridružio (1924) svakoj čestici, koja se giba. On polazi od relativističke formule E = mc2, gdje je dana masa m, koja pripada energiji E, te od izraza za energiju fotona E = hv. Spajanjem tih dviju formula dobivamo polaznu točku teorije L. de Brogliea: E = mc2 = hv. Svakoj čestici mase m pridružen je periodički pojav frekvencije v. U prostoru, u kojem čestica miruje, t. j koji se zajedno s česticom giba, ta formula glasi: E0 = m0c2 = hv0. L. de Broglie uzima, da je periodički pojav u tom prostoru čisto titranje. Pri prielazu u prostor, u kojem se čestica giba, valja se poslužiti Lorentzovom transformacijom (→ relativnost), pa se onda periodički pojav u tom prostoru predoči kao val. Dužina λ tog vala dana je izrazom λ = h/mv, gdje je v brzina čestice, a brzina vala formulom u — c2/v. Dakle je brzina tih valova veća od brzine svjetlosti c.
W. Elsasser je upozorio (1925), da bi se materijski valovi mogli eksperimentalno pokazati kao difrakcija i interferencija elektronskih i atomskih zraka, t. j. u pojavima, značajnim za valove.
10. DIFRAKCIJA (OGIB) I INTERFERENCIJA ELEKTRONSKIH ZRAKA nađena je eksperimentalno g. 1927. Davisson i Germer pustili su uzki svežanj sporih elektrona, da pada okomito na plohu niklenog kristala, pa su iztraživali, kako se oni od njega odrazuju. Našli su, da za izvjestne brzine elektrona postoje u prostoru povlašteni smjerovi, u koje se elektroni osobito jako odbijaju. To se može protumačiti time, da se elektronski valovi, nastali ogibom na atomima kristala, u tim smjerovima interferencijom pojačavaju. Iz razporeda atoma na površini kristala i povlaštenog smjera odraza mogli su Davisson i Germer odrediti dužinu vala elektronskih zraka. Ta se izvrstno slaže s onom, što je predviđa teorija de Brogliea. Razlog, zašto se takvo odbijanje elektronskih zraka dobiva samo za izvjestne brzine elektrona, t. j. samo za odabrane dužine elektronskih valova, jest u tome, što u pojavu sudjeluju i valovi nastali ogibom na atomima izpod površine kristala. Ako se uzme u obzir i dubinski razpored atoma u kristalu, to se mogu teoretski odrediti te odabrane dužine elektronskih valova. Ove se međutim ne slažu osobito s eksperimentalno nađenima, jer se u teoriji zasada ne može dovoljno uzeti u obzir zamršeno električko polje, koje vlada u unutarnjosti kristala.
 Sl. 6.
Sl. 6. Sl. 8.
Sl. 8.Ogib brzih elektrona pokazao je G. P. Thomson (1927) pustivši, da uzki svežanj elektronskih zraka prolazi kroz mikrokristalinični kovinski listić vrlo malene debljine (oko 10-6 mm). Zrake zatim padaju na fotografsku ploču, okomitu na njihov prvotni smjer. Osim središnje mrlje, u kojoj zgađaju ploču one elektronske zrake, koje nisu promienile smjera, pokaže se još nekoliko krugova, od zraka odklonjenih ogibom na kristalićima listića. Sl. 6 jedna je snimka G. P. Thomsona (→ Debye-Scherrerova metoda).
Sl. 7 prikazuje ogib elektronskih zraka dobiven njihovim prolazom kroz vrlo tanki listić tinjca (snimili Finch i Wilman). Taj ogib odgovara ogibu svjetlosti na ukrštenim mrežicama (→ difrakcija), a dobiven je na način Laueovih diagrama kod rentgenskih zraka.
H. Borschu uspjelo je (1940) dobiti s elektronskim zrakama ogib Fresnelova tipa na rubu poluravnine (sl. 8, povećano oko sto puta).
 Sl. 7.
Sl. 7.11. »VALNI PAKET« je zamisao E. Schrödingera, u kojoj su zorno spojene obje predočbe o elektronu: tjelešce i val. Materijski valovi elektrona imadu po toj zamisli amplitudu različnu od ništa samo u jednom malenom djeliću prostora; u njemu je dakle zgusnuta sva energija tih valova. Prema tome se taj djelić prostora može smatrati kao mjesto tjelešca. Takav valni paket nije međutim jednostavan valovit pojav, nego je sastavljen od jednostavnih valova, koji izpunjavaju čitav, prostor. Dužine tih valova poprimaju sve moguće vriednosti iz jednog uzkog područja oko dužine vala, koja prema de Broglieu pripada tjelešcu, što se giba brzinom v. Ovi se valovi poništavaju interferencijom posvuda osim u gore spomenutom djeliću prostora, u kome grade valni paket. Premda pojedini jednostavni valovi putuju brzinama, koje su prema teoriji de Broglieovoj veće od brzine svjetlosti c, ipak se valni paket giba, kako potanje razmatranje pokazuje, brzinom v tjelešca. Nažalost, valni paket povećava s vremenom svoj obujam i — kako vrieme napreduje — znademo sa sve manjom točnošću mjesto čestice. Na granici pak dvaju područja, na kojoj se materijski valovi lome i reflektiraju, razpada se u dva valna paketa. To su potežkoće, radi kojih se valnom paketu ne može pripisati objektivni značaj.
12. VALNA MEHANIKA i njoj ravnopravna kvantna mehanika odriču se zorne predočbe o gibanju elektrona u atomima. — E. Schrödinger je osnovao (1926) valnu mehaniku vođen paralelizmom, koji postoji između klasične mehanike i geometrijske optike (Hamilton, 1828). Geometrijska optika vriedi uz uvjet, da su leće i predmet, od kojega valja načiniti sliku, veliki prema dužini vala upotrebljene svjetlosti. Pri prielazu na sitne predmete treba se poslužiti optikom, koja vodi računa o valovitoj naravi svjetlosti. Geometrijska optika je tek granični slučaj valne. Schrödinger uzima, da je i mehanika, koja vriedi za velika tjelesa, tek granični slučaj valne mehanike, koju valja upotrebiti, ako se radi o sitnim tjelešcima i malenim prostorima, kao što je elektron unutar jednog atoma. Osnovnu jednačbu svoje valne mehanike dokučio je Schrodinger služeći se osnovnom jednačbom valne optike te paralelizmom klasične mehanike i geometrijske optike. Dužina vala, koja u tu jednačbu ulazi, izražena je kinetičkom energijom čestice, njenom masom i Planckovom konstantom, a poklapa se s dužinom materijskog vala, što ga je de Broglie pridružio čestici, ali uz uvjet, da je brzina čestice malena prema brzini svjetlosti c. Razlog je tome, što je Schrodinger pošao od klasične mehanike, koja je granični slučaj relativističke, ako su brzine tjelesa malene prema c.
U atomu ima elektron i potencialnu energiju, jer na njega djeluje električko polje ostalih dielova atoma. Ta potencialna energija ulazi u osnovnu jednačbu valne mehanike, jer se na njezin račun može povećati kinetička energija elektrona, dakle smanjiti dužina materijskog vala. U slučaju vodikova atoma potječe to polje od jednoga protona. Za funkciju, koja predočuje val u osnovnoj jednačbi, nalazi se diskretan niz jednoznačnih i neprekidnih rješenja, koja su karakterizirana cielim brojevima, t. zv. kvantnim brojevima. Svakom od ovih rješenja pripada posve određena energija elektrona. Bohrov kvantni uvjet ovdje je suvišan, jer se diskretan niz stacionarnih stanja nadaje sam od sebe. Iz dobivenih valnih funkcija grade se vjerojatnosti, da se elektron nalazi u nekom dielu prostora, odnosno da prieđe iz jednog stacionarnog stanja u drugo (Born, 1927).
13. RELATIVISTIČKA VALNA MEHANIKA je ona, koja zadovoljava načelo relativnosti. — Već je sam Schrödinger pokušao (1926) uskladiti osnovnu jednačbu valne mehanike s teorijom relativnosti. Jednačba, do koje je došao, nije međutim dala dobar rezultat za finu strukturu vodikovih crta, dok je Sommerfeldovo relativističko proširenje Bohrove teorije, kako je prije spomenuto, bilo u tom pogledu u skladu s izkustvom. Odatle je Dirac zaključio, da Schrödingerova relativistička valna jednačba nije osnovna jednačba relativističke valne mehanike. Služeći se četverorednim matricama Dirac je uspio (1928) razciepiti relativističku Schrödingerovu diferencialnu jednačbu, koja je drugog reda, u četiri jednačbe prvog reda. U Diracovu prikazu ima zato valna funkcija četiri komponente. Dvie od ovih odnose se na elektrone pozitivne kinetičke energije, a dvie, što se izprva smatralo velikom potežkoćom, na elektrone negativne kinetičke energije.
Promatra li se elektron s pozitivnom kinetičkom energijom, a s takvima se u izkustvu susrećemo, to iz Diracove teorije sliedi, da on ima, kad nalazi u elektromagnetskom polju, osim potencialne energije, radi svojeg električkog naboja, još i potencialnu energiju, radi svojega magnetskog momenta. Za veličinu tog momenta teorija daje baš jedan Bohrov magneton. Isto tako sliedi iz Diracove teorije, da elektronu pripada i spin u iznosu, što ga zahtieva hipoteza Goudsmita i Uhlenbecka. Tako se ova hipoteza izvodi posve prirodno iz Diracove valne mehanike.
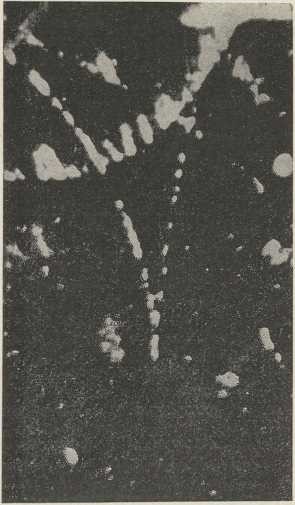 Sl. 9.
Sl. 9.Dirac nije mogao zanemariti rješenja s negativnom kinetičkom energijom elektrona, jer teorija daje konačnu vjerojatnost, da elektron pozitivne energije, kad se nalazi u polju neke atomske jezgre, prieđe u stanje negativne energije, a razlika se energije između tih stanja pretvori u foton. Kako bi na taj način domalo svi elektroni iz svieta nestali, prešavši u »podsviet«, to Dirac uzima, da su stanja negativne energije već zaposjednuta, pa po Paulijevu načelu takav prielaz nije moguć. Prielaz jednog elektrona iz podsvieta u sviet moguć je u polju atomske jezgre, ako mu jedan energijom dovoljno bogat foton preda svoju energiju. Nastala šupljina među elektronima negativne energije ima pozitivni električki naboj i energiju, t. j. masu, običnog elektrona. Ta se dakle šupljina vlada poput pozitivno električkog elektrona, pozitrona. Viek je pozitrona međutim kratak. Čim naiđe na elektron, koji pripada jednom atomu, poništi se s ovim, i njihova se energija pretvori u energiju fotona.
Potežkoće s elektronima negativne energije i teorija šupljina našle su sjajnu potvrdu u eksperimentalnom odkriću pozitrona (Anderson, 1932) i u pretvorbi fotona u elektron i pozitron (t. zv. dvojci; I. Curie i F. Joliot, 1933). Sl. 9 je snimka supruga Curie-Juliot, koja prikazuje pretvorbu jednog fotona gama-zraka ThC′′ u elektron i pozitron. Staze ovih učinjene su vidljivima metodom Wilsonove komore, dok je staza fotona, koji je doletio odozdo, nevidljiva. Budući da je u prostoru komore bilo pobuđeno magnetsko polje, to su staze elektrona i pozitrona svinute na protivne strane.
LIT.: R. A. Millikan, The Electron, 1924; P. A. M. Dirac, Die Prinzipien der Quantenmechanik (prievod s englezkog), 1930; A. Sommerfeld, Atombau und Spektrallinien, I. sv., 1931, II. sv., 1939; M. von Laue, Materiewellen und ihre Interferenzen, 1944; Sir J. Jeans, The New Background of Science, 1933; H. A. Bauer, Grundlagen der Atomphysik, 1938; Grimsehl-Tomaschek, Lehrbuch der Physik III., 1943.V. L-ć.
Elektron, negativni i pozitivni. Gdjekada se naziv elektron upotrebljava ne samo za česticu u katodnim zrakama, atomskoj ljusci i t. d., već i za pozitron (→ čestice elementarne). Prva se čestica onda zove negativni elektron, druga pozitivni elektron.St. H.
Elektron, težki bio je prvobitni naziv za mezotron (→ čestice elementarne).St. H.
Elektroni i kemijska svojstva elemenata. Već se davno naslućivalo, da elektrika sudjeluje u izgradnji materije. Helmholtz je tumačio Faradayeve zakone s pomoću atoma elektrike. U elektrolitima, kod prolaza struje, putuju pozitivni i negativni atomi elektrike zajedno sa svojim tvarnim nosiocima, a takve čestice zovemo ionima. Metalna vodljivost stoji naprotiv u gibanju slobodnih negativnih elementarnih čestica elektrike. Te su negativne čestice po priedlogu Stoneya nazvane »elektronima«. Kasnije se došlo do spoznaje, da su elektroni uobće sastavni dio atoma, pa su dobiveni i u slobodnom stanju. Bilo je čudno, što se ne mogu dobiti i atomi pozitivne elektrike u slobodnom stanju, već uviek vezani uz atome materije. Razlog je u tome, što se slobodni elektroni mogu lako odieliti od materije, jer dolaze u ovoju atoma. Kada se elektroni odiele od materije, zaostaje isti iznos pozitivne elektrike na ostatku atoma. Zato je dugo bila uzaludno tražena slobodna elementarna čestica pozitivne elektrike — pozitron, dok je nije našao Anderson (1932).
Danas nam je poznat ne samo naboj elementarnih čestica elektrike — elektrona i pozitrona — već i njihova masa, koja je 1840 puta manja od mase najlakšeg atoma, t. j. vodikova atoma.
Atomi kemijskih elemenata nisu homogeno izpunjeni materijom, već se sastoje iz pozitivne jezgre i negativnih elektrona, koji se brzo giblju u okolišu jezgara. Ti elektroni mogu biti bliže ili dalje u »ovoju« oko jezgara. Kako su elektroni lagani, to je gotovo sva masa atoma koncentrirana u jezgri. Pozitivna jezgra i elektroni u ovoju privlače se elektrostatskim silama. Coulombove sile privlačenja i centrifugalna sila elektrona drže se u ravnoteži, pa odatle zaključujemo, da se elektroni moraju oko jezgre gibati po određenim stazama. Elektroni su porazdieljeni u elektronskom ovoju oko jezgre u pojedinim slojevima ili ljuskama. Tako dolazimo do slike o izgradnji atoma ili do atomskog modela, kako su ga zamislili E. Rutherford (1911) i N. Bohr (1913).
Najjednostavnije je izgrađen vodikov atom, koji ima u jezgri jedan proton, a u ovoju samo jedan elektron (→ atom).
Govorili smo o elektronu kao čestici negativne elektrike. Prema novijem naučavanju atomske fizike elektronima pripisujemo i valnu prirodu. Kao što svietlo nastupa dualistički, kao valovita pojava i kao gibanje čestica (korpuskularno gibanje), tako pripada i materiji, dakle i elektronima, taj čudni dualizam (De Broglie, 1924). To je odkriće dalo povoda postavljanju kvantne i valne mehanike. W. Heisenberg je uspio s pomoću valne mehanike protumačiti teoriju atomskog ovoja i ukloniti nepodudaranja. Današnja fizika s jednakim pravom upotrebljava valnu i korpuskularnu sliku atoma. Zapravo je slika atoma valne i kvantne mehanike matematička tvorevina, veoma zamršena i gotovo bez ikakve zornosti. Zato se u kemiji radije služimo korpuskularnom slikom atoma. Na taj su nam način razumljiva kemijska svojstva pojedinih elemenata, njihova periodičnost i valjanost ili valencija.
Ako promotrimo periodički sustav elemenata (v.), vidjet ćemo, da se u 1. periodi nalaze samo dva elementa: vodik i helij. U 2. periodi dolazi osam elemenata: litij, berilij, bor, ugljik, dušik, kisik, fluor i neon. Obje se periode završavaju s plemenitim plinom. Helij ima dva elektrona u vanjskoj ljuski, a neon osam. Takve su ljuske stabilne, one su popunjene elektronima. Zato su plemeniti plinovi kemijski indiferentni. Atomi, koji se nalaze prije i poslije plemenitih plinova u periodičkom sustavu, nemaju vanjsku ljusku popunjenu elektronima, zato su izvrgnuti promjenama i mogu kemijski reagirati. O vanjskim dakle elektronima ovise kemijska svojstva elemenata i njihova valencija. Zato takve vanjske elektrone zovemo »elektronima valencije«. Element fluor ima u svojoj vanjskoj ljuski 7 elektrona, nema dakle još jednoga elektrona, da bude podpuna ljuska plemenitog plina. Doista, atom fluora lako prima taj jedan elektron, pa u otopinama dolazi redovno kao negativni jednovaljani ion. Naprotiv, elementi, koji imaju u vanjskoj ljuski samo jedan elektron (to su elementi na početku perioda: vodik i alkalijske kovine), lako odpuštaju taj elektron, pa postaju jednovaljani elektropozitivni ioni. Odatle sliedi, da će se ti elementi osobito rado spajati s halogenim elementima, koji lako primaju jedan elektron, da popune svoju vanjsku ljusku na 8 elektrona. Tako nastaju spojevi fluorovodik (HF), natrijev fluorid (NaF), natrijev klorid (NaCl) i dr. U 3. periodi, koja počinje s natrijem, a završava se s argonom, nalazi se također 8 elemenata. Nakon treće periode postaje sustav nešto zamršeniji, jer u 4. periodi, koja počinje s kalijem, a završava se s plemenitim plinom kriptonom, ima 18 elemenata, a isto ih je toliko i u 5. periodi, koja počinje s rubidijem, a završava se s ksenonom. U 6 periodi nalaze se, počevši od cesija do plemenitog plina radona (emanacije), čak 32 elementa. Posljednja, 7. perioda, nije podpuna, ona se završava s elementom uranom, koji ima redni broj 92.
Razpodjelba elektrona
| Element |
Redni broj (broj protona) |
Broj elektrona |
| |
1.nutar. ljuska |
2. ljuska |
3. ljuska |
| Vodik |
1 |
1 |
— |
— |
| Helij |
2 |
2 |
— |
— |
| Litij |
3 |
2 |
1 |
— |
| Berilij |
4 |
2 |
2 |
— |
| Bor |
5 |
2 |
3 |
— |
| Ugljik |
6 |
2 |
4 |
— |
| Dušik |
7 |
2 |
5 |
— |
| Kisik |
8 |
2 |
6 |
— |
| Fluor |
9 |
2 |
7 |
— |
| Neon |
10 |
2 |
8 |
— |
| Natrij |
11 |
2 |
8 |
1 |
| Magnezij |
12 |
2 |
8 |
2 |
| Aluminij |
13 |
2 |
8 |
3 |
| Silicij |
14 |
2 |
8 |
4 |
| Fosfor |
15 |
2 |
8 |
5 |
| Sumpor |
16 |
2 |
8 |
6 |
| Klor |
17 |
2 |
8 |
7 |
| Argon |
18 |
2 |
8 |
8 |
i. t. d.
Promotrimo li kao primjer atom ugljika, vidjet ćemo, da dolazi na šestom mjestu u periodičkom sustavu elemenata, dakle ima u jezgri 6 protona i 6 elektrona u ovoju. Ovi se elektroni ne nalaze svi na istoj ljuski. Što je atom veći, to više ima protona u jezgri i elektrona u ovoju, koji se giblju po određenim ljuskama u određenim udaljenostima. Tako na primjer najteži atom urana (redni broj 92) ima 92 protona u jezgri i 92 elektrona, koji kruže porazdieljeni na 7 ljusaka.
Brojevi su elektrona u pojedinim popunjenim ljuskama sliedeći: 2, 8, 18, 32. Oni se pokoravaju jednostavnom matematičkom odnosu: 2.12 (=2), 2.22 (= 8), 2.32 (= 18), 2.42 (=32). Kad je ljuska popunjena određenim maksimalnim brojem elektrona, dolaze daljnji elektroni na novu vanjsku ljusku. Prva unutarnja ljuska može imati najviše 2 elektrona, sliedeća 8 i t. d., dok vanjska ljuska može imati od 1 do najviše 8 elektrona.
Rekli smo već, da o vanjskim elektronima ovise kemijska svojstva, karakter i valencija atoma. Prema tome će oni elementi, koji imaju u izvanjskoj ljuski isti broj elektrona, biti kemijski veoma slični. Takvi elementi idu u istu skupinu periodičkog sustava.
Kada dva elementa stvaraju međusobno spoj, nastaje promjena u podjeli elektrona u vanjskoj ljuski. Prema teoriji Kossela i Lewisa (1916), koju su izradili na temelju Bohrova atomskog modela, spajaju se kovine i nekovine tako, da njihovi atomi prelaze u ionsko. stanje, t. j. elektropozitivni elementi predaju svoje labilno vezane elektrone valencija elektronegativnim metaloidima. Pritom nastaje u vanjskim elektronskim ljuskama poredak kao kod plemenitih plinova. Pozitivni i negativni ioni imaju konfiguraciju plemenitog plina, redovno s 8 elektrona u vanjskoj ljuski. Na pr. kod jednovaljanih alkalijskih kovina nalazi se u vanjskoj ljuski samo jedan elektron valencije, koji se lako odcjepljuje, pa zaostaje jednovaljani pozitivni ion. Poredak je elektrona u ovoju tog iona sada jednak poredku elektrona u predhodnom atomu plemenitog plina. Razlika je samo u jezgri i masi. Ion ima veću masu i pozitivni naboj, uvjetovan od protona jezgre. Zbog većeg centralnog naboja imaju elektronske ljuske u ionu manje polumjere od polumjera plemenitih plinova. Lewis je kasnije (1923) pokušao protumačiti i stvaranje nepolarnih molekula (na pr. Cl2, C2,H6 i t. d.) s pomoću t. zv. zajedničkih elektronskih parova (oktetska teorija). Prema tome bi atomi obćenito nastojali prieći kod spajanja u stanje, kakvo imaju plemeniti plinovi. Oni naime nemaju labilno vezanih elektrona valencije. Njihovi su atomi omeđeni vrlo stabilnom elektronskom ljuskom.
Ovako možemo iz poredka elektrona u ovoju atoma tumačiti svojstva i ponašanje različitih elemenata i nastajanje njihovih spojeva. Zato je elektronska teorija postala važna i u anorganskoj i organskoj kemiji.M. D-ć.
Elektronska optika 1. je nauka, koja se bavi dobivanjem slika pomoću gibanja elektrona u električkim i magnetskim poljima. Geometrijska e. o. promatra elektron kao električku česticu i proučava geometriju njegovih staza u ovim poljima; ona odgovara geometrijskoj optici svjetlosti. Valna e. o. uzima u obzir valnu narav elektrona (→ Broglie 3) kod stvaranja slike; ona odgovara fizikalnoj optici svjetlosti, posebno ogibu. Za raztvornu moć elektronskooptičkog uređaja vriedi Abbeova relacija iz optike svjetlosti: dmin = λ : (n • sin u), gdje je n • sin u numerička apertura, ako za λ stavimo De Broglieovu valnu dužinu. Međutim optičke pogrješke najboljih elektronskih leća i uz neobično malene numeričke aperture (reda veličine 10-2 do 10-3), kakve se upotrebljavaju, još uviek bitno više utječu na točnost točkastog oslikavanja današnjim elektronskim uređajima nego Abbeova relacija, tako da je raztvorna moć najboljih elektronskih nadmikroskopa znatno izpod teoretske granice određene De Broglievom valnom dužinom i numeričkom aperturom. Zato u elektronskoj optici prevlađuju gledišta geometrijske optike, pa se pod e-om o-om obično razumieva geometrijska.
Slično kao u optici svjetlosti slika u običnom smislu rieči nastaje, ako se zrake elektrona, koji izlaze iz jedne točke u ravnini okomitoj na os elektronsko-optičkog sustava, opet sastaju u jednoj točki druge takve ravnine. Da bi slika bila slična predmetu, potrebno je, da sve točke slike leže u meridianskim ravninama pripadnih točaka na predmetu. Kod elektronsko-optičkih sustava s magnetskim lećama moramo ovaj preduvjet sličnosti proširiti time, da točke slike moraju biti zakrenute za isti kut prema meridianskim ravninama pripadnih točaka predmeta.
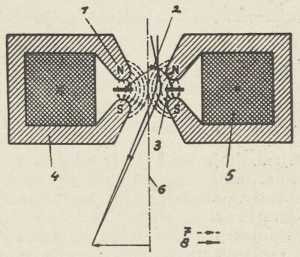 Sl. 1. Shema magnetske leće.
Sl. 1. Shema magnetske leće.
1. polni krajevi; 2. predmet;
3. prstenasti zapor; 4. željezni oklop;
5. navoji uzvojnice; 6. optička os leće;
7. magnetske silnice; 8. staze dvaju elektrona
iz vrha predmetaPravi početak geometrijske e-e o-e treba računati od dviju radnja H. Buscha iz g. 1926 i 1927. Busch je dokazao, da aksialno simetričko magnetsko polje jedne kratke uzvojnice djeluje na staze elektrona u svežnju katodnih zraka, malo nagnutih prema osi uzvojnice (paraksialne zrake), kao kratka sabirna leća na svjetlost, te da za sliku, dobivenu takvom magnetskom lećom, vriedi optička jednačba leće: 1/a + 1/b = 1/f, gdje je f žarištna daljina magnetske leće, određena njenim magnetskim poljem, dok su a i b daljine predmeta i slike od sredine leće. U sl. 1 shematski je prikazan osni presjek magnetske leće poboljšanog oblika s kratkom žarištnom daljinom. To je upravo tip novijih magnetskih leća, kakve se ugrađuju u cievima elektronskih mikroskopa. Da bi, uzprkos prostranosti navoja uzvojnice (ukršteno izcrtani pravokutnici), magnetska leća bila kratka, uzvojnica je zatvorena u željeznom oklopu, osim jednog prstenastog prociepa na unutrašnjem dielu plašta. Horizontalni crni potezi unutar tog prociepa označuju prstenasti zapor za zaustavljanje elektrona razpršenih na objektu. U shemi su također prikazane magnetske silnice i staze elektrona, koji stvaraju sliku predmeta, projicirane na ravninu crtnje. Buschova formula za žarištnu daljinu glasi:
\(\;\;\displaystyle f=\cfrac{4v^2}{\gamma^2}:\int_{-\infty}^{+\infty}H^2(z)\,dz\)
, gdje su v i γ brzina i specifički naboj elektrona, dok H(z) prikazuje jakost magnetskog polja uzduž osi simetrije z. Preglednija je približna formula, koju su dali Knoll i Ruska: f ≈ C ∙ Vd/i2N4, gdje su: C jedna konstanta, V napetost ubrzanja elektrona, d srednji promjer uzvojnice, dok je i jakost struje u uzvojnici s brojem uzvoja N. Prema tome mienjanjem napetosti V i jakosti i možemo žarištnu daljinu magnetske leće mienjati u dosta širokim granicama. Sličnu promjenljivost žarištne daljine imaju i elektrostatske elektronske leće. U tome je bitna razlika prema lećama u optici svjetlosti. Iz formula za f sliedi ujedno, da magnetska leća uviek djeluje kao sabirna leća. Povećanje je P = b/a kao u svjetlostnoj optici. U sl. 2 prikazana je magnetska leća nešto starije izvedbe. Visina prstenastoga zračnog prociepa može se na njoj mienjati; tim se mienja debljina leće.
 Sl. 2.
Sl. 2.Djelovanje magnetske leće na zrake elektrona, koje idu ponešto koso prema osi leće, sastoji se i u tome, da se zraka spiralno zakreće, pa je slika zakrenuta prema predmetu. Ovo se zakretanje dade više ili manje kompenzirati sustavom dviju ili triju leća sa suprotnim magnetskim poljima, jer suprotna magnetska polja izvode suprotna zakretanja, dok su jakosti 1/f nezavisne o smjeru polja te se približno zbrajaju.
Potrebno je iztaknuti jednu temeljnu razliku između leće u svjetlostnoj optici i leća u e-oj o-i. Svojstva svjetlostne leće osnivaju se na lomu svjetlosti, t. j. na naglom skoku u brzini svjetlosti na graničnim plohama leće. U e-oj o-i ovom je načelu približno odgovarala samo elektrostatska leća s električkim dvoslojem, koju su 1932 izradili Knoll i Ruska, a koja je ubrzo iztisnuta elektrostatskim lećama bez diskontinuiteta. Naprotiv, značajka je magnetskih polja, koja djeluju kao kratka elektronska leća, njihova kontinuirana prostorna promjenljivost, a to je značajka i elektrostatskih polja kod elektrostatskih leća, koje su razvijene poslije dvoslojne leće. Magnetske leće čak uobće ne mienjaju brzine elektrona, koji prolaze kroz njih. Djelovanje spomenutih novijih elektrostatskih leća temelji se na kontinuiranoj promjeni brzine elektrona. U svjetlostnoj bi im optici odgovarala leća izgrađena od nehomogenog sredstva, kojemu bi indeks loma postepeno rastao prema sredini leće. Takvo je svojstvo u manjoj mjeri ostvareno u tankom površinskom sloju Zeissovih t. zv. T-leća.
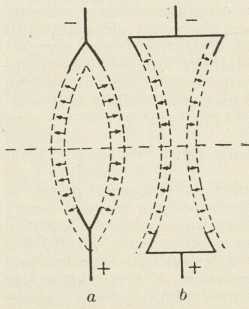 Sl. 3. Elektrostatske dvoslojne leće;
Sl. 3. Elektrostatske dvoslojne leće;
a) sabirna leća, b) raztresna leća.
Strjelice naznačuju smjer polja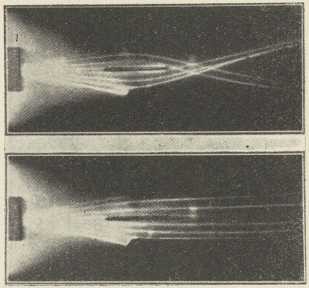 Sl. 4. Skretanje zraka elektrona u
Sl. 4. Skretanje zraka elektrona u
elektrostatskoj cilindričkoj lećiSvako rotaciono-simetrično električko polje djeluje kao elektrostatska elektronska leća na elektrone, koji se gibaju pod nevelikim nagibom prema njegovoj osi simetrije. Takvo se polje ostvaruje električkim kondenzatorima s aksialnom simetrijom. Dvoslojna leća bila je kondenzator od tanke žične mreže, u kojem je unutrašnja mreža bila na pozitivnoj, a vanjska na negativnoj napetosti. Ovakva leća djeluje kao sabirna ili kao raztresna leća, prema tome, ima li žični dvosloj konveksan ili konkavan oblik (sl. 3a, b). Bolja je bila leća od Brüchea i Johannsona (1932) u obliku cilindričkog kondenzatora; njezin se oblik razabira u srednjem dielu snimaka u sl. 4; one prikazuju staze elektrona prije i poslije prolaza kroz presjek takve leće. Elektrostatska elektronska leća, kakva se danas upotrebljava, t. zv. pojedinačna leća, dvostruki je kondenzator u obliku triju koaksialnih zaslonskih otvora jednog za drugim, od kojih je unutrašnji na pr. na negativnoj napetosti, a dva su vanjska na istoj pozitivnoj napetosti, dok su lievo i desno prostori s jednakim potencialom, što u svjetlostnoj optici odgovara prostorima konstantnog indeksa loma. Ovakva je leća najprije opisana u jednom francuzkom patentu iz 1928; proučavali su je 1930 Davisson i Calbick, ali je njezina uloga u napredku e-e o-e započela istom 1932, kad su je nezavisno odkrili s jedne strane Knoll i Ruska, s druge strane Brüche i Johannson. Leća s cilindričkim kondenzatorom i pojedinačna leća uviek djeluju kao sabirna leća.
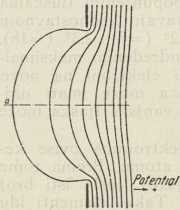 Sl. 5.
Sl. 5.Dademo li kovnoj ploči s okruglim otvorom ili kovnom prstenu neku električku napetost, dok su jakosti polja nalievo i nadesno nejednake, već električko polje oko takvog otvora, koje je aksialno simetrično, a nesimetrično prema ravnini ploče ili prstena, djeluje kao elektronska leća. To je zaslonski otvor. U sl. 5 prikazane su njegove ekvipotencialne plohe u aksialnom presjeku. Za njegovu žarištnu daljinu vriedi formula:
\(\qquad\qquad\displaystyle \cfrac{4\,\varphi_0}{E_1-E_2},\)
gdje je φ0 napetost na zaslonskoj ploči, a E1 i E2 su jakosti polja na jednoj i na drugoj strani. Zbog izraza u nazivniku zaslonski otvor djeluje za E1 > E2 kao sabirna, za E1 < E2 kao raztresna leća.
 Sl. 7.
Sl. 7.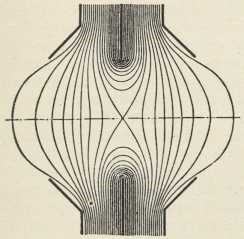 Sl. 6.
Sl. 6.Sl. 6 prikazuje aksialni presjek kroz poboljšani oblik spomenute pojedinačne leće i kroz njezine ekvipotencialne plohe. Zadatak je e-e o-e izračunati staze elektrona u takvu polju ograničujući se na paraksialne staze. Jakost ovakve leće dana je ovom formulom:
\(\qquad\qquad\displaystyle \cfrac1f=\cfrac1{8\sqrt{V}}\int_{-\infty}^{+\infty}\cfrac1{\sqrt{(V+U)^3}}\;\left(\cfrac{\partial U}{\partial z}\right)^2\; dz,\)
gdje su V napetost, koja određuje brzinu elektrona, a U napetost na osi leće. Sl. 7 prikazuje pojedinačnu leću za visoku napetost u izvedbi AEG-a.
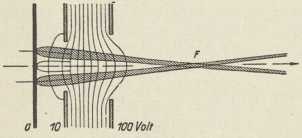 Sl. 8.
Sl. 8.Dva koaksialna zaslonska otvora na nejednakim napetostima, smještena u prostoru bez polja, daju treću vrst elektrostatske leće, imerzionu leću, koja je uviek sabirna. Ovamo pripada u prvom redu imerzioni objektiv kod elektronskog mikroskopa. Kod njega zaslonski otvor, bliži katodi, koja emitira, ili iztraživanom objektu, ne graniči s prostorom bez polja, nego je prema njima na malenoj napetosti. U sl. 8 prikazani su presjek kroz ekvipotencialne plohe takva objektiva i staze dvaju elektronskih snopova iz katode.
Povisiujemo li negativnu napetost negativnog zaslonskog otvora pojedinačne leće, umanjuje se broj elektrona, koji prodiru kroz leću. Tim se postupkom dade ostvariti u e-oj o-i iris-otvor svjetlostne optike. Dobije li povišena negativna napetost toliku vriednost, da elektroni ne mogu prodrieti kroz leću, oni se reflektiraju, pa elektrostatska leća djeluje kao elektronsko ogledalo. Ovakvu vladanju leće nema analogije u svjetlostnoj optici.
Kod elektronskih leća susrećemo 5 istih pogrješaka, koje poznajemo kod svjetlostnih leća u monohromatskoj svjetlosti. To su: sferna aberacija, astigmatizam, svodolikost slike, izobličenost i koma. Kod magnetskih leća pridolaze još tri pogrješke, kojima je izvor u zakretanju elektronskih staza. To su: anizotropna koma, anizotropni astigmatizam i anizotropno zakretanje slike. Potežkoće kod uklanjanja ovih pogrješaka sile na primjenu vrlo malenih apertura. Ako napetost, koja daje elektronima brzinu, koleba za više od l%, javljaju se nove pogrješke, koje odgovaraju hromatskoj aberaciji leća u svjetlostnoj optici.
Ulogu prizme iz svjetlostne optike, t. j. odklon zrake i disperziju, imaju u elektronskoj optici homogeno transverzalno električko polje i homogeno transverzalno magnetsko polje. Približno tako djeluju odklonske pločice ili odklonske uzvojnice kod Braunove cievi ili katodnog oscilografa. Disperzija elektronskih staza sastoji se u tome, da njihov odklon u takvim poljima zavisi o brzini elektrona, pa se elektroni različitih brzina gibaju u različito zakrivljenim stazama. U ovom je odvajanju po brzinama na prvi mah razlika između disperzije u svjetlostnoj optici i disperzije u e-oj o-i. Dodirnu točku uzpostavljamo kvalitativno preko De Broglieove jednačbe; ali ostaje razlika u tom, što elektroni veće brzine, t. j. s kraćom valnom dužinom vala pratioca, dobivaju manje odklone. Prostrana homogena transverzalna električka i magnetska polja imaju osim toga i svojstvo fokusiranja, jer takva polja elektrone, koji se gibaju slabo divergentnim početnim smjerovima jednakim brzinama, sjedinjuju u jednoj točki, odnosno u jednom pravcu. U svjetlostnoj optici slično svojstvo imaju prizme s konveksnim plohama.
2. Analogno načinu izražavanja, uvrieženom u primienjenoj svjetlostnoj optici, upotrebljava se kadkad izraz »elektronska optika« i kao skraćeni tehnički naziv za elektronsko-optički sustav primienjen u nekom elektronskom aparatu.
LIT.: H. Busch, Ann. d. Phys. (4) 81, 974, 1926 i Archiv f. Elektrot. 18, 583, 1927; H. Busch-E. Brüche, Elektronenoptik, Leipzig 1937; M. v. Ardenne, Elektronen-Übermikroskopie, Berlin 1940.M. K.
Elektronske cievi, naprave na načelu strujanja elektrona u visokom vakuumu (t. j. prostoru po mogućnosti podpuno lišenom zraka) s vrlo mnogobrojnim primjenama, osobito u radiotehnici, električkoj reprodukciji zvuka i sl. Redovito se e. c. izvode kao stakleni baloni, u koje se, već prema predviđenoj upotrebi, smjeste dvie, tri ili više naročito građenih i naročito razpoređenih elektroda s priključcima izvedenima kroz stienke balona u vanjski prostor. Kroz mali cjevasti otvor, t. zv. izsisnu cjevčicu, balon se nakon ugradnje elektroda (upotrebom dobrih zračnih sisaljki uz istodobno tjeranje zaostalih plinova sa staklenih stienki i elektroda primjenom vrućine) nadasve pomno evakuira, na pr. toliko, da od svake miliarde molekula zraka ne zaostane više nego jedna, i nakon toga se izsisna cjevčica zataljivanjem hermetično zatvori. Visoki se vakuum osigurava i prikladnim absorpcionim sredstvima, t. zv. getterima, stavljenima u samu ciev. Po potrebi se stakleni balon cievi, zbog toga, da se sprieči skupljanje električkih naboja na njegovim nutarnjim plohama, iznutra pocrni slojem ugljena, a uz to se, zbog zaštite od izvanjskih elektrostatskih polja, izvana »metalizira« slojem kovne (bakrene ili cinčane) boje sa zaštitnom prevlakom pokosti. Priključci, koji su izvedeni iz pojedinih elektroda, skupe se u normiranom razpoređaju na »podnožju« cievi iz prikladne tvari, koja električki izolira, a za pojedine se elektrode dovedu do kapice na vrhu cievi. Mnogo se grade danas i »metalne« e. c. s čeličnim evakuiranim balonima, kroz koje se dakako provodi elektrodskih priključaka izvedu električki izolirano.
U bitnosti se kod e-ih c-i uviek radi o strujanju elektrona između dvie elektrode u posve određenom (a ne i obrnutom) smislu, naime od t. zv. katode prema t. zv. anodi, koja je s obzirom na katodu jako pozitivno električki nabijena; međutim kod većine e-ih c-i smjesti se između katode i anode još jedna ili više elektroda, t. zv. mrežica ili rešetki, koje kroz svoje otvore više ili manje propuštaju elektrone, što struje iz katode, no svojim negativnim ili pozitivnim električkim potencialom ujedno slabe ili pojačavaju, odnosno djelomično na sebe svraćaju struju elektrona s katode. Najjednostavnije su e. c. prema tome cievi bez mrežice, samo s katodom i anodom, t. j. cievi s dvie elektrode ili diode; sliede dalje cievi s tri elektrode ili triode s katodom, jednom mrežicom i anodom, zatim cievi sa četiri elektrode ili tetrode s katodom, dvie mrežice i anodom, pa pentode, heksode, heptode i oktode s tri, četiri, pet i šest mrežica, t. j. s pet, šest, sedam i osam elektroda.
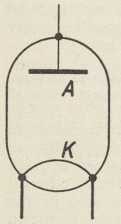 Sl. 1.
Sl. 1.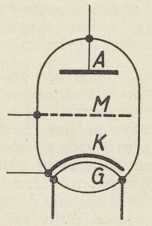 Sl. 2.
Sl. 2.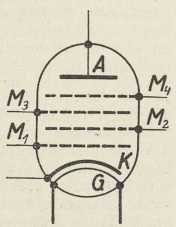 Sl. 3.
Sl. 3.Budući da katoda mora biti izvor elektrona, ona se gradi tako i kod pogona se cievi podržava u takvu stanju, da doista daje iz sebe elektrone. U tu se svrhu (služeći se pojavom izbacivanja ili emisije elektrona iz vrućih vodiča u vakuumu) katodi može dati oblik tanke žice s priključcima s oba kraja, tako da se ona može jače ili slabije žariti direktno električkom »strujom grijanja« iz posebnoga pomoćnog izvora struje (na pr. »baterije grijanja«, koja se pozitivnim i negativnim polom priključi na katodne priključke). No katodni se sustav može izvesti i s grijačem odieljenim od katode, na pr. s grijačem u obliku spiralizirane volframove žice, preko kojeg se izolirano natakne niklena cjevčica, prevučena izvana djelotvornom oksidnom pastom, koja emitira elektrone. Tada se strujom grijanja (na pr. iz »transformatora grijanja« priključena na mrežu izmjenične struje) neposredno žari samo grijač, a katodi, u ovom slučaju tek indirektno grijanoj grijačem, ostaje samo još funkcija elektrode, tako da joj postane dovoljan jedan izvanjski priključak. Prema tomu ima »direktno grijanih« cievi s dva priključka do oba kraja katode i »indirektno grijanih« s tri priključka katodnoga sustava, dva do grijača i jednim do katode (v. u sl. 1 simbol direktno grijane diode s katodom K i anodom A, sa svega 3 priključka, te u sl. 2 simbol indirektno grijane triode s grijačem G, katodom K, mrežicom M i anodom A, s ukupno 5 priključaka, napokon u sl. 3 shemu indirektno grijane heksode s mrežicama M1 do M4 i svega 8 priključaka).
Praktički se kao material katoda, koji emitira elektrone, uzimao najprije volfram, koji je trebalo usijavati do biologa žara, zatim volfram s primjesom torija, koji dovoljno emitira već kod žutoga žara, dok najmanje energije struje grijanja troše suvremene katode s oksidima barija i sl. na prikladnom nosiocu, koje je dosta tek tamno crveno žariti. Pored ovih potonjih katoda, običajnih kod malih prijamnih cievi (za aparate za primanje radija, za električka pojačala zvuka i dr.), susreću se međutim još uviek u posebnim slučajevima i katode iz volframa ili iz toriranog volframa (kod velikih emisionih cievi postaja za davanje radiosignala i kod visokonaponskih ventila za rentgenske uređaje za visoki istosmjerni napon).
 Sl. 4.
Sl. 4.Katodu okružuje kod trioda mrežica, a ovu opet anoda; kod tetrodâ do oktodâ oko katodi najbliže »prve« mrežice ovija se »druga« i tako redom, a sve okružuje anoda. Mrežice su obično zavojnice od molibdenske žice s gušćim ili rjeđim zavojima, a anode su iz masivnog lima ili gusto tkane mreže od nikla, željeza, tantala i dr. Pogled kroz unutrašnjost jedne prijamne cievi (pentode) daje rentgenska snimka reproducirana u sl. 4; unutar staklenog balona, kome je dolje i izsisna cjevčica, razabiru se elektrode s pet priključaka (dva od grijača, jedan zajednički od katode i treće mrežice, te po jedan od druge mrežice i anode), izvedenih na podnožje, i s jednim priključkom (od prve mrežice) izvedenim na kapicu cievi. Kod pogona potrebni su mrežicama, osim signala, koji se puštaju, da djeluju na određenu mrežicu ili mrežice, stalni negativni ili pozitivni predhodni potenciali u odnosu prema katodi, t. zv. mrežni prednaponi, a anode pogotovo trebaju, da bi ostale jako pozitivno nabijene prema katodi unatoč tome, što pristižu negativni naboji u obliku elektrona s katode, određene predhodne pozitivne napone, t. zv. anodne napone. Zato se kod upotrebe e-ih c-i moraju obćenito predvidjeti, osim izvora struje grijanja, koji e-m c-ima daje potrebiti »napon grijanja«, još i izvori spomenutih napona. Kod već zastarjeloga baterijskog pogona uzimaju se osim »baterije grijanja« u obliku akumulatora još »baterija mrežnih prednapona« i »anodna baterija«; obje se potonje obično sastave iz malih suhih elemenata i kombiniraju u jedno. Kod suvremenog se pogona iz mreže izmjenične struje dobivaju sva tri izvora transformiranjem napona mreže s jedne strane na napon grijanja, koji se kod indirektno grijanih cievi uviek, a kod direktno grijanih u posebnim slučajevima može bez daljega preudešavanja upotrebiti, a s druge na napon, koji dalje »izpravljen« na prikladan način (na pr. diodama, kako će se odmah razložiti) i »izglađen« (upotrebom svitaka i kondenzatora) postane istosmjeran i toliko stalan, da može služiti za prednapone mrežicama i anodama. Kod malih aparatura, na pr. prijamnika radija, ovakve naprave za pogon e-ih c-i izmjeničnom strujom nisu skupe i ne uzimaju mnogo struje iz električke mreže, dok je dakako baš obrnuto kod jakih emisionih postaja radija, gdje treba njihovim posredstvom privesti emisionim cievima velike električke snage i k tomu pri vrlo visokim anodnim i mrežnim naponima.
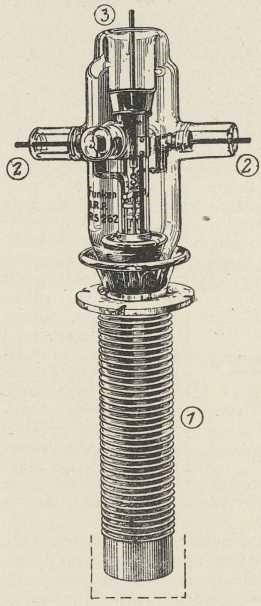 Sl. 5.
Sl. 5.Treba još primietiti, da se u e-im c-ima javljaju gubitci energije i s njima vezana ugrijavanja elektroda. Poimence se od ukupne električke snage, crpene iz izvora anodne struje, jedan dio bezkoristno troši u vezi s bombardiranjem anoda brzim elektronima, koji su dojurili s katode, pa anode postanu u pogonu kadkad vrlo vruće. A vruće, nego odgovara crvenom žaru, anode ne smiju postati. Zato se cievima s velikim ugrijavanjem anoda — poimence diodama za izpravljanje izmjenične struje, konačnim cievima u pojačalima i malim emisionim cievima — anode pocrnjuju. To znatno povećava obteretivost cievi, jer olakšava izsijavanje topline s anode. A kod velikih se emisionih cievi anode čak izvedu vakuumski sigurno pritaljene na staklo, tako da su odkrivene prema vani, pa se mogu »umjetno hladiti« posebnim uređajima s kruženjem hladne vode. Tako trioda za 25 kilovata snage na sl. 5, u naravi gotovo metar visoka, ima razhladnim rebrima snabdjevenu anodu 1, oko koje se kod upotrebe pričvrsti posuda s cirkulacijom vode (njezin donji dio je u slici crtkano markiran); razabiru se još oba katodna priključka 2 i mrežni priključak 3.
Za teoriju i primjene e-ih c-i bit će koristno najprije razmotriti diode (sl. 1). Njihova se upotreba ndaje sama iz okolnosti, da u njima struje elektroni, dakle negativni naboji, samo u smislu katoda-anoda. Diode mogu dakle, s obzirom na to, da je običajno smjerom električne struje nazivati smjer, kojim bi se gibali pozitivni naboji, propuštati samo struje u smislu anodakatoda, pa prema tomu mogu služiti kao »izpravljači« izmjeničnih struja u istosmjerne. Za takvu su službu diode u mnogim prilikama prikladne. Kraj male tromosti elektrona, koju možemo zanemariti, one jednako dobro izpravljaju »nizkofrekventne« struje, t. j. struje iz razsvjetne mreže i uobće struje »tonskih« frekvencija, kao i »visokofrekventne« signale »valova nosilaca« radija s često mnogo tisuća i više puta bržim titraj ima. Kod dioda u prvoj upotrebi određenije se govori o izpravljačkim diodama ili visokovakuumskim izpravljačicama ili kenotronima, a u rentgenskoj tehnici, gdje se radi o propuštanju u jednom i zaustavljanju u protivnom smislu strujâ kod napose visokih napona, i o visokonaponskim ventilima. Naprotiv se u slučaju izpravljanja »moduliranih« (t. j. u ritmu titrajâ prenašanih zvukova jačanih i slabijenih) visokofrekventnih signala radija govori radije o »detekciji«, i pri tomu upotrebljavane diode zovu se pobliže detektorskim diodama.
U pogledu izpravljačica vriedno je primietiti, da sama jedna izpravljačica može, dakako, izpravljati tek »poluvalno«, t. j. propuštati na pr. pozitivne i zaustavljati negativne polovice titraja izmjenične struje; no upotrebom dviju izpravljačica, priključenih na transformator s dva sekundarna namotaja, i to jednim glavnim, koji treba da dade izpravljanu struju i mora imati odvojak u sredini, i drugim pomoćnim, koji odmah daje struju grijanja objema izpravljačicama, moguće je izpravljati i »punovalno«, t. j. tako, da se upotrebe obje polovice vala izmjenične struje. Po ovom načelu rade već spomenute naprave za priključak prijamnih radio-aparata na izmjeničnu struju, pri čemu se obje izpravljačice obično spoje po sl. 6 u jednu dvostruku s dvie anode A1 i A2 i zajedničkom katodom K. Upotrebljeni mrežni transformator obično se onda snabdije na sekundarnoj strani i jednim daljim, dakle trećim namotajem, iz kojega dobivaju struju grijanja i različite cievi same prijamne aparature u užem smislu. Mrežni prednaponi dobivaju se međutim kadkad i bez naročitih izvora struje po načelu gubitka napona u odporima protjecanima strujom (»automatski prednaponi«).
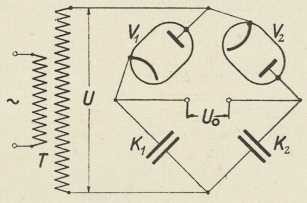 Sl. 7.
Sl. 7.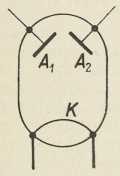 Sl. 6.
Sl. 6.Punovalno izpravljanje izmjeničnih struja vrši se kadkad također spojevima sa četiri izpravljačice kod jednofaznog priključka, a sa šest kod trofaznog priključka; u potonjem je slučaju izpravljena struja već i bez glađenja prilično stalna. Posebno se ovako, upotrebljavajući četiri ili šest visokonaponskih ventila, mogu proizvoditi visoki istosmjerni naponi za pogon rentgenskih cievi, iako se tu više upotrebljavaju na pr. spojevi po sl. 7 sa sama dva ventila V1 i V2, no kombinirana i s dva kondenzatora K1 i K2. Kod spoja po sl. 7 izlazi istosmjerni napon U0 između 1 i 2 priključene rentgenske cievi gotovo dvaput tolik kao »maksimalni« ili »tjemeni« iznos Um, dakle malone triput tolik kao »efektivni« iznos U izmjeničnoga napona proizvedenoga sekundarno visokonaponskim transformatorom T, koji se primarno priključi na električku mrežu (vriedi relacija Um = 1,414 • U). Povišenje napona postizava se spojem po sl. 7 zbog toga, što se kondenzatori K1 i K2 preko ventila V1 i V2 naizmjence nabijaju iz transformatora T i prikladno izbijaju kroz rentgensku ciev; uz transformator T za sekundarno 40 hiljada volta postizavaju se tako na rentgenskoj cievi izpravljeni naponi znatno iznad 100 hiljada volta.
Ugrijavanja anoda kod izpravljačica obično su znatna i samo su ekvivalent električke snage Ua • Ia, koja se troši u samim izpravljačicama s toga razloga, što prolaz određene anodne struje Ia uvjetuje određen »gubitak napona« Ua u izpravljačici. U prvo je vrieme bilo nejasno, zašto već kod povoljno malenih pozitivnih napona anode prema katodi ne struje elektroni, potrebni, da se podržava ma koja anodna struja sve do najviše uz određenu užarenost katode moguće struje, t. zv. struje zasićenosti, kod koje bi se trošili svi elektroni, koje izbacuje katoda kod dane temperature, odnosno dane struje grijanja. Bliža razmatranja pokazala su, da iznos anodne struje Ia najprije raste s povećavanjem anodnoga napona diode Ua po posve određenom zakonu neke vrste parabole, točnije: parabole reda 1,5, dakle po »formuli prostornoga naboja«:
Ia = K • Ua1,5
gdje je K konstanta određena geometrijskim odnosima katode i anode. Tomu je pojavu uzrok djelovanje naboja onih elektrona, koji se u danom momentu nađu u prostoru između katode i anode pa odbijaju one, koji bi iza njih išli prema anodi; istom se visokim pozitivnim anodnim naponom toliko svlada spomenuto djelovanje, da Ia dostigne iznos struje zasićenosti Is te ostaje na tom iznosu kod nepromienjene temperature katode, ma koliko dalje rastao anodni napon. Grafički predočeno krivulja s ordinatama Ia i abscisama Ua, t. zv. Ia-Ua-krivulja, uzdiže se najprije po zakonu parabole reda 1,5, da u nekoj izvjestnoj visini Is, ovisnoj kod dane cievi samo o struji grijanja, postane horizontalna. Kod jače struje grijanja postane dakako Is veće, pa krivulja postaje u većoj visini vodoravna. Za iznos struje zasićenosti Is vriedi izraz:
Is = A • e -b/T • T2 • S
gdje S znači površinu i T stupnjeve aibsolutne skale temperature (za 273 povišene stupnjeve Celzijeve skale) užarene katode, e bazu prirodnih logaritama 2,718..., te A i b konstante. Uz Is u amperima i S u cm2 je A = 60,2, dok b varira s djelotvornom tvari katode, pa je na pr. za volfram b = 52600. Iz ovog izraza lako je vidjeti, da već neznatno jača grijanja katode daju znatna povišenja struje zasićenosti.
Uz detektorske diode spominjemo još da su se diode za svrhe detekcije upotrebljavale, dok još nije bilo cievi s mrežicama, iako su im tu bili jaki takmaci, doduše manje pouzdani, ali zato jednostavniji i osjetljiviji »kristalni detektori« (→ detektor). Kasnije su se za detekciju cievima počele s osobitim uspjehom upotrebljavati, i to na različite načine, triode, dok se danas kod prijama radiofonije u moderniziranom obliku pored trioda u funkciji detektora opet dosta ciene i detektorske diode. Poimence se diode upotrebljavaju u superheterodinim prijamnicima (»superima«) za svrhe prve i druge detekcije i za svrhe automatske regulacije jakosti reprodukcije zvuka na iznos, neovisan o variranju jakosti primanih radiosignala. Kod supera su, protivno nego kod običnih prijamnika sa samo jednom detekcijom, potrebne dvie detekcije, jer se kod ovih aparata primanim visokofrekventnim signalima radia kratkih ili srednjih dužina vala, predhodno pojačanima ili nepojačanima, primiešaju titraji ponešto druge dužine vala proizvedeni posebnim olscilatorskim spojevima. Iz dobivene se smjese prvom detekcijom dobivaju signali transponirani na određenu znatno smanjenu visoku frekvenciju, t. zv. međufrekventni signali, koji se lako pojačavaju; pojačani pak međufrekventni signali tek ponovnom detekcijom postaju signali u ritmu bezžično prenašanih zvukova, dakle tonfrekventni signali, koji se opet mogu kao takvi dalje pojačavati, prije nego se puste da djeluju na zvučnik.
Prelazeći na cievi s mrežicama svrnut ćemo pažnju naročito na njihove najosnovnije i po načinu funkcioniranja najpreglednije reprezentante: triode.
Budući da se mrežici M (sl. 2) može dati povoljni prednapon Ug, očito se ne samo anodom, nego i mrežicom dade utjecati na struju elektrona s katode. Posebno kod negativne, i zbog toga za elektrone odbojne mrežice elektroni će težko prolaziti kroz otvore mrežice prema pozitivnoj anodi, pa će negativni prednaponi mrežice doći do izražaja u obliku smanjenja anodne struje prema onoj uz mrežicu na prednaponu Ug = 0. Kako je pak mrežica znatno bliže katodi nego anoda, čak svaki volt mrežnog napona dolazi do izražaja kao nekoliko volta anodnoga, na pr. 1 V, primienjen na mrežicu, kao 25 V primienjenih na anodu, u kome se slučaju veli, da ciev ima faktor pojačavanja m = 25 ili prohvat D = 1/m = 1/25 = 0,04, odnosno u postotcima D = 4%. Drugim riečima: kod cievi sa m = 25 ili D = 0,04 račun bi dao istu anodnu struju, na pr. 0,006 A ili 6 mA (6 miliampera), uz primienjenih +100 V na anodi i 0 V na mrežici kao i uz primienjenih + 150 V na anodi i —2 V na mrežici, odnosno 200 ili 250 V na anodi kraj —4 ili —6 V na mrežici.
Budući da se tu radi o tri veličine triode u međusobnim odnosima, moguće je predočiti ovisnosti anodne struje Ia o mrežnom prednaponu Ug i anodnom Ua tek rojem krivulja, bilo tako, da se nacrtaju Ia-Ug-krivulje uz iznose Ua, iste za svaku krivulju, bilo opet tako, da se nacrtaju Ia-Ua-krivulje za pojedine Ug. Roj krivulja prvog tipa predočen je na sl. 8.
Kako se vidi, ista struja 6 mA može se odčitati na krivulji s Ua = 100 V kod Ug = 0 V kao i na krivuljama s Ua = 150, 200 i 250 V kod Ug= —2, —4 i —6 V, što s obzirom na malo prije spomenuti primjer o m i D = 1/m znači, da se krivulje na sl. 8 odnose na ciev s m = 25 ih D = 0,04.
Međutim još se dvie dragocjene okolnosti dadu pročitati iz »karakteristika« u sl. 8. Da izlaganja budu jednostavnija, ograničimo se samo na ono radno područje, gdje karakteristike na sl. 8 smijemo smatrati pravocrtnima, paralelnima i jednoliko razmaknutima. U tom slučaju vidimo ponajprije, da se karakteristike uzdižu s određenim priklonom prema osi abscisa, t. j. s određenim omjerom prirasta struje Ia prema pripadnom prirastu napona Ug, pa se za promatrano područje taj omjer pridaje samoj triodi pod imenom strmine S. Tako se iz sl. 8 razabira, da na karakteristici s anodnim naponom 200 V porastu anodne struje od 6 mA na 10 mA, t. j. za 4 mA ili 0,004 A, odgovara porast mrežnog prednapona od —4 V na —2 V, t. j. za 2 V, tako da bi strmina bila: S = 0,004/2 = 0,002 »ampera po voltu« (=2 »miliampera po voltu«).
No još se i to razabira, da bi trioda s karakteristikama po sl. 8 uz stalan mrežni prednapon na pr. —2 V propuštala kod anodnih napona 200 V i 150 V anodne struje 10 mA, odnosno 6 mA, t. j. da bi na 50 V prirasta anodnog napona reagirala sa 4 mA ili 0,004 A prirasta anodne struje. Međutim uobće je prirodno omjer prirasta napona prema pripadnom prirastu struje (pomišljajući na temeljni Ohmov zakon o električkim strujama) nazvati odporom, pa je običaj posebno promatrani takav omjer, pripisujući ga cievi, zvati unutarnjim odporom R0 triode; u danom slučaju bilo bi: R0=50/0,004 = 12500 oma.
Lako se uvjeriti, da vriedi jednostavna formula: D • S • R0 = 0,04 • 0,002 • 12500 = 1; čak ovakva relacija između triju karakterističnih veličina triode vriedi i obćenito na svakom dielku područja karakteristika, makar se spomenute veličine i mienjale od dielka do dielka. Prema tomu se kod poznate dvie od triju veličine D, S i R0 treća može računski naći.
Na podlozi karakteristika lako je moguće razabrati najosnovniju funkciju triode, njezinu upotrebu kao pojačalo signala. Zbog zanemarive tromosti elektrona pojačavani signali mogu biti i vrlo brzo promjenljivi, tako da se triodama mogu pojačavati signali radija: a) prije detekcije, dok su još »visokofrekventni« (posebno kod superheterodina također i nakon prve detekcije, ali prije druge detekcije, dok su još »međufrekventni«), kao i b) nakon detekcije (kod superheterodina nakon druge detekcije), kad su već tonfrekventni; u slučajevima a) govori se o visokofrekventnom (i posebno o »međufrekventnom«), a u slučajevima b) o nizkofrekventnom pojačavanju; ovo potonje primjenjuje se i kod električkih naprava za reprodukciju zvuka.
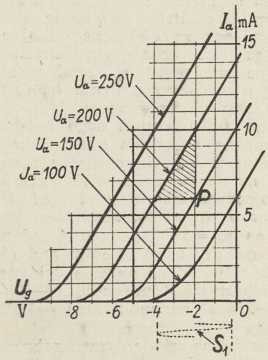 Sl. 8.
Sl. 8.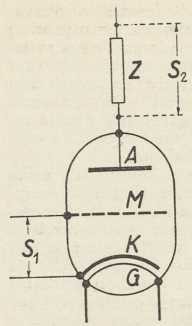 Sl. 9.
Sl. 9.I visokofrekventna kao i nizkofrekventna pojačavanja mogu se praktički vršiti različnim postupcima, pri čemu se u posebnim slučajevima triode zamjenjuju za pojedine svrhe prikladnijim cievima s više mrežica, na pr. tetrodama ili pentodama. No osnovno načelo ostaje kod svih pojačavanja cievima uviek isto i može se razabrati iz obćenite sheme pojačavanja triodom u sl. 9. Kako se vidi, u anodni strujni krug triode s predpostavljenim karakteristikama po sl. 8 uključen je neki potrošač struje, t. zv. »anodni odpor« Z, koji će tek u najjednostavnijem slučaju biti obični omski odpor od R oma, dok će redovito biti neki »složeni odpor« za izmjenične struje (na pr. bit će to zavojnica u spoju s kondenzatorom, odnosno zavojnica sama za sebe ili transformator) prilagođen frekvenciji pojačavanih signala. Ako se sad pojačavani izmjenični signal S1 , koji je crtkano naznačen na sl. 8, primieni između mrežice i katode cievi iz sl. 9, sa Ua i Ug, prije toga prikladno udešenima — na pr. po sl. 8 sa Ua = 150 V i Ug = —2 V, na točku P karakteristike 150 V s abscisom —2 V — superponirat će se vremenski promjenljivi iznosi napona signala S1 stalnom naponu Ug, pa će se korespondentno signalu kolebati ukupni napon mrežice, a s njim i anodna struja cievi. Posebno bi se kod izmjeničnoga napona iz sl. 8 s amplitudom 1,8 V, dakle s maksimumom +1,8 V i minimumom —1,8 V, napon mrežice mienjao između —2 + 1,8 volta i —2 —1,8 volta, dakle između —0,2 V i —3,8 V, što bi izazvalo posve izvjestna mienjanja anodne struje. No anodna struja kod spoja po sl. 9 teče i kroz anodni odpor Z, pa mienjanja anodne struje moraju doći do izražaja u mienjanjima napona između krajeva odpora Z, koja će kod odabranoga radnog područja, kao na sl. 8, i kod prikladnog Z biti vjerna, no u isti čas i mnogostruko uvećana reprodukcija S2 signala S1 primienjena na mrežicu. Promatranim cievnim spojem »pojačan« je dakle prvobitni signal, i pojačani se signal može, prikladnim načinom odvojen s anodnoga odpora, podvrgnuti nakon ovakva »jednostepenog« pojačavanja ponovnom pojačavanju idućim »stepenom« pojačavanja, i opet po sl. 9, i tako dalje. Postignuto »pojačanje«, t. j. omjer p amplitudâ signala S2 i S1 zavisi o upotrebljenoj cievi i odabranom anodnom odporu, različitom kod različitih tipova pojačavanja. Osobito je lako p izračunati uz predpostavku omskog odpora iznosa R oma kao anodnog odpora; ako su m i R0 faktor pojačavanja i unutarnji odpor upotrebljene triode, vriedi za p jednostavna formula: p = m • R/(R0 + R), po kojoj bi se kod ovakva »odpornog pojačavanja« na pr. uz ciev sa m = 20 i R0 = 10.000 oma, a kod R = 30 000 oma, postiglo kod jednostepenoga pojačavanja »pojačanje« p = 15, kod dvostepenog pojačanje p2 = 15 • 15 = 225, i tako dalje. Treba još reći, da osim opisanoga najjednostavnijeg tipa pojačavanja i pripadnih t. zv. naponskih pojačala ili A-pojačala (s izkorišćenjem samo pravocrtnih dielova karakteristika i istodobnim ograničenjem na područja negativnih mrežnih napona za cielo vrieme djelovanja pojačavanog signala) postoje još dva načelno drugčija i znatno zamršenija tipa pojačavanja, i po tomu još t. zv. B-pojačala i C-pojačala. Treba li na pr. iz konačnog stepena nizkofrekventnog pojačavanja izvući mnogo snage za pogon ovećeg zvučnika, uzet će se koje od B-pojačala sa znatno više negativnim mrežnim prednaponima nego kod A-pojačala, a time izazvanim »izobličenjima« pojačavanog zvuka predusrest će se upotrebom dviju konačnih cievi »u protudjelovanju« (push-pull). U visokofrekventnom području, kod pojačavanja titraja u velikim emisionim postajama, uz B-pojačala ima i C-pojačalâ s još jače negativnim mrežnim prednaponima. Međutim ono, što je rečeno o A-pojačalima, dovoljno načelno osvjetljuje uobće mogućnosti pojačavanja triodama.
Od trioda u funkciji pojačala samo je jedan korak do njihove primjene kao oscilatora, t. j. proizvoditelja visokofrekventnih i nizkofrekventnih struja. Pomislimo, da se jedan dio energije mrežnim signalom S1 izazvanog variranja anodne struje sa anodnog odpora Z triode prenese natrag na mrežni krug t. zv. reakcijom, t. j. prikladnim induktivnim, kapacitivnim ili sličnim djelovanjem između anodnog i mrežnog kruga, te da se tim dobije na mrežici baš tolik i takva predznaka signal S1, kojega je podržavanje upravo potrebno za izazivanje onih variranja struje u Z. U tom slučaju ciev sama sebi proizvodi signal S1 pa i ne treba za podržavanje spomenutih variranja nikakva vanjskog signala: ciev se sama »uzbudi« na titranja, koja se podržavaju na račun energije crpene iz izvora anodne struje.
Vidjeli smo triode kao pojačala različitih tipova i kao oscilatore, a mogli bismo ih opisati i kao modulatore u službi moduliranja visokofrekventnih titraja zvučnim frekvencijama kod bezžične telefonije, kao što smo ih već prije spomenuli, pored dioda, kao detektore (ima čak dva tipa detekcije triodama: detekcija »audionima« i detekcija »anodnim detektorima«). Načelno se pak od trioda u njihovim glavnim funkcijama ne razlikuju ni cievi s više mrežica, koje tek, pored »upravljačke« mrežice (kadkad 1 dvie takve) s funkcijom upravljanja anodnom strujom s pomoću signalâ na mrežici kao i kod trioda, imaju još mrežice s naročitim zadatcima, t. zv. »zaslonske« i »zahvatne« mrežice, te po tomu u mnogim prilikama daju bolje rezultate. Kraj ovako raznovrstnih funkcija pronalazak i postepeni razvoj e-ih c-i, razumievajući tu i izpravljačice, prirodno je izazvao revolucionarni napredak cielih područja elektrotehnike, u prvom redu radiotehnike. U radiotehnici suvremene bezžične postaje za davanje i nisu drugo nego uređaji, gdje se samouzbuđenim oscilatorskim cievima proizvedeni visokofrekventni titraji, po potrebi modulirani mikrofonskim strujama posredstvom modulatorskih cievi, postepeno pojačavaju sve većim i većim cievima u stepenima sve veće snage; tako se konačno antenskom krugu dobivaju jake visokofrekventne struje, kojih energiju antena izsijava u prostor u obliku valova radija. Slično e. c. danas podpuno vladaju i na prijamnoj strani, pa će recimo osjetljiv suvremeni super imati na pr. najprije ciev za visokofrekventno pojačavanje antenom uhvaćenih bezžičnih signala, zatim oscilatorsku ciev pa ciev za »miešanje« primanih signala s oscilatorskima u međufrekventne (prvi detektor), onda cievi za međufrekventno pojačavanje te ciev za konačnu detekciju (drugi detektor) kao i one za nizkofrekventno pojačavanje; k tomu još treba pored cievi za posebne svrhe (na pr. indikaciju točnog udešavanja na primani val) dodati dvostruku izpravljačicu naprave za pogon ciele aparature izmjeničnom strujom. Kao ciev za miešanje mogla bi se na pr. uzeti heksoda po sl. 3 sa M1 i M3 kao upravljačkim i M2 i M4 kao zaslonskim mrežicama: na M1 bi se primienili primani, a na M3 oscilatorski titraji. No oktodom bi se mogla nadomjestiti u isti mah i ciev za miešanje i oscilatorska ciev, kao što se uobće pojedinim posebnim ili kombiniranim cievima pridaje više zadaća. Važne su još primjene e-ih c-i: pojačavanje zvuka u telefoniji i električkoj reprodukciji zvuka (električki gramofoni, naprave sa zvučnim prienosima i sl.) pa izpravljanja izmjeničnih struja u visokonaponskim napravama. Mnogo se e. c. primjenjuju i u električkoj mjernoj tehnici.
S poviestnoga gledišta primietimo, da je pojave izbacivanja elektrona iz usijanih vodiča iztraživao među prvima Richardson, a probleme utjecaja prostornih naboja i potrebu najviših vakuuma u e-m c-a izticao je uz ostale Langmuir. Za uvođenje mrežica u e. c. zaslužan je osobito Lee de Forest, za misao reakcije Meissner.
LIT.: H. Barkhausen, Elektronenröhren, 3. i 4. izd., Leipzig 1932—38; F. Vilbig, Lehrbuch d. Hochfrequenztechnik, 3. izd., Leipzig 1941; J. Lončar, Konstrukcije radiostanica, 2. izd., Zagreb 1931.J. L.
Elektronski mikroskop je elektronsko-optički uređaj, kojim se pomoću elektronskih zraka dobiva povećana slika mikroskopskog predmeta (→ elektronska optika 1). Ako povećanje nadilazi najveća povećanja, koja se dadu postići svjetlostnim mikroskopom, e. m. se naziva nadmikroskopom. Nastojanje, da se njim dobiju što bolje slike u što većem povećanju, bilo je izravnim povodom brzom razvoju elektronske optike.
Mogućnost dobivanja slike pomoću elektrona u gibanju osnovana je dualnom prirodom elektrona. Njegova priroda električke korpuskule određuje pravocrtno gibanje rojeva elektrona u prostorima bez električkog i bez magnetskog polja kao i geometriju njihovih staza u takvim poljima. Valna priroda elektrona u gibanju određuje njihovu sposobnost ogiba i stvaranja optičkih slika. Stalnost valne dužine u elektronskoj je optici još većma preduvjetom za monohromatičnost ogiba i razgovjetnost slike nego u svjetlostnoj optici. Stalnost valne dužine elektronskog vala pratioca uvjetovana je stalnošću brzine elektrona, a ova je određena stalnošću električke napetosti. Na taj je način temeljni uvjet, koji ima izpuniti uređaj e-g m-a, razpolaganje s izvanredno stalnim izvorom visoke jednake napetosti. U geometrijskoj elektronskoj optici ovo dolazi do izražaja u formulama za žarištnu daljinu magnetskih i elektrostatskih leća. Snošljivi obseg kolebanja napetosti ravna se po trajanju ekspozicije snimke, jer je kod dužih ekspozicija veća vjerojatnost, da će se u visini napetosti na mikroskopu odraziti i spora kolebanja napetosti gradske mreže. Izkustvom je utvrđeno, da do trajanja ekspozicije 10s kolebanja visoke jednake napetosti smiju iznositi najviše 0,1% kolebanja gradske napetosti, a iznad 10s imaju se sniziti na manje od 0,001%. Kod magnetskih leća pridolazi i zavisnost jakosti leće o kvadratu jakosti struje u uzvojnici, pa mora biti osigurano i strogo održavanje struje na stalnoj jakosti.
Prema tome e. m. sastoji se od visoko evakuirane cievi, u kojoj mlaz elektrona dobiva jednakom visokom napetošću između anode i katode veliku jednaku brzinu. Različite vrsti e-og m-a razlikuju se elektronsko-optičkim sustavom primienjenim između anode i mjesta, gdje nastaje slika. Vakuum ima biti viši od 1 • 10-4 mm Hg; inače se javljaju smetnje od prostornog naboja nastalog ionizacijom ostataka plina.
Visina potrebne anodne napetosti većinom leži između 30 kV i 100 kV. Jakost je anodne struje 10 do 100 puta manja nego kod rentgenskih cievi. Odatle sliedi, da okolina mora biti dobro zaštićena od rentgenskih zraka, što izbijaju iz svih dielova, u koje udaraju elektroni. Osobito se valja pobrinuti, da se uklone promjenljiva magnetska polja, okomita na os mikroskopa. U tu je svrhu ciev mikroskopa oklopljena jednostrukim i dvostrukim cilindrima od feromagnetičkih slitina velike permeabilnosti.
Slike, dobivene e-im m-om, nadmašuju svjetlostnim kontrastima one, koje su dobivene svjetlostnim mikroskopom. Ovome je razlog u tome, što kontrasti kod oslikavanja elektronima dolaze samo od razlika u razpršavanju elektrona na različitim točkama objekta, odnosno u emisijskim mikroskopima (v. niže pod 1 i 4) u različitim emisijskim sposobnostima različitih mikropodručja katode. Da ovi kontrasti ne bi bili u snimkama pokvareni razpršavanjem elektrona u osjetljivom sloju fotografske ploče, upotrebljavaju se posebne ploče, kod kojih je to razpršavanje svedeno na najmanju mjeru. To su t. zv. Schumannove ploče, na kojima je tanak osjetljivi sloj bez želatina.
Pod raztvornom moći mikroskopa razumieva se najmanji razmak na objektu, koji se kod najvećeg polučenog povećanja poveća na 0,3 mm. Dok se raztvorna moć svjetlostnog mikroskopa zaustavlja na odprilike 200 mμ, elektronski nadmikroskop uz prosijavanje objekta spustio je tu granicu (do kraja 1940) prosječno do na 5 mμ, a u pojedinim slučajevima na 3 mμ; ovo odgovara izravnom povećanju od 100.000 puta. Vrlo oštre snimke dopuštaju još naknadna povećanja svjetlostnim putem. Tim su otvorena nova područja u iztraživanju žive i nežive tvari. Napokon je Ardenne nedavno (1944) svojim najnovijim elektronskim nadmikroskopom polučio raztvornu moć 1,2 mμ.
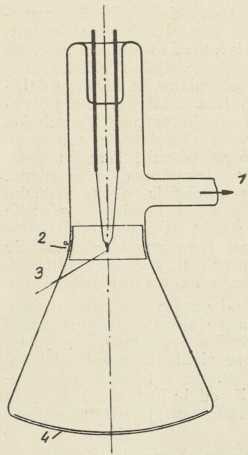 Sl. 1. – 1. 1. Spoj sa sisaljkom. 2. anoda.
Sl. 1. – 1. 1. Spoj sa sisaljkom. 2. anoda.
3. katoda. 4. fluoroscentni zastorDok se kod svjetlostnog mikroskopa primjenjuju samo dvie metode za dobivanje povećane slike: metoda prosijavanja objekta kod običnog mikroskopa i metoda odbijene svjetlosti kod mikroskopa za iztraživanje kovnih površina — omogućuje elektronska optika više načina, da se dobije povećana slika. Tome je razlog s jedne strane kratka De Broglieova valna dužina brzih elektrona, a s druge strane mogućnost, da se dimenzije elektronskog izvora elektronsko-optičkim putem umjetno umanje do 105 puta. Tako se prve tri vrste e-og m-a u opisima, koji sliede, osnivaju na pravocrtnom gibanju elektrona u prostoru bez električkih i magnetskih polja. Vrste su poredane uglavnom tako, da s rednim brojem raste sličnost s normalnim svjetlostnim mikroskopom.
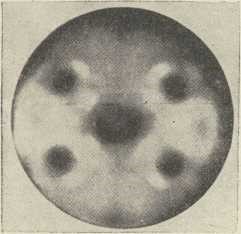 Sl. 2. Emisija elektrona iz ploha Volframova monokristala.
Sl. 2. Emisija elektrona iz ploha Volframova monokristala.
Povećanje blizu 100 000x. Snimka od E. W. Müllera1. Elektronski nadmikroskop emisijom autoelektrona (R. P. Johnson i W. Shockley, 1936; E. W. Müller, 1937) osniva se na sposobnosti vrlo jakih električkih polja (reda 106 do 107 volt/cm), da omoguće izlazak elektrona iz kovnih površina vrlo velike zakrivljenosti (autoelektroni). Bitni dielovi ovog nadmikroskopa u Müllerovoj izvedbi prikazani su shematski u sl. 1. Katoda (3) je vrlo oštar šiljak od volframa ili molibdena, gladko zašiljen kemičkim postupkom, a polumjer zakrivljenosti na vrhu reda je veličine 10-4 mm. Ciev je evakuirana do vrlo visokog vakuuma (kod 1 je spoj sa sisaljkom), a žice, koje vode do katodnog šiljka, služe za to, da se užarivanjem u vakuumu uklone iz šiljka tragovi adsorbiranih plinova. Anoda je prsten (2) uz stienu cievi oko katode, a napetost između nje i katode reda je 10 kV. Zakrivljena ploha cievi nasuprot vrhu katode obložena je fluorescentnim slojem (4). Brzi elektroni, koji izlaze iz katode, gibaju se pravocrtno i stvaraju na fluorescentnom sloju centralnom projekcijom sliku elektronske emisije iz vrha katode. To je jedina primjena ovog mikroskopa. Povećanje je određeno omjerom polumjera zakrivljenosti fluorescentnog zastora i vrha katodnog šiljka. Sl. 2 prikazuje jednu snimku emisije autoelektrona iz diela jednoga sitnog volframova monokristala; povećanje je blizu 100.000x.
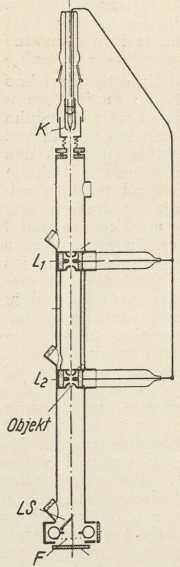 Sl. 3.
Sl. 3. Sl. 4. Dio oklopa jedne diatomeje.
Sl. 4. Dio oklopa jedne diatomeje.
Povećanje 4200x. Snimka od H. Boerscha2. Nadmikroskop pomoću projekcije sjene (H. Boersch, 1939). Slika, koju daje ovaj nadmikroskop, vrlo je povećana sjena mikroskopskog objekta projicirana u prostoru bez električkog polja iz točkastog elektronskog izvora izvanredno malenih dimenzija. Kao ovakav izvor djeluje vrlo umanjena elektronska slika primarnog elektronskog izvora. To je t. zv. elektronska sonda. Mikroskopski uređaj prikazan je shemom u sl. 3. Elektronsko-optičke leće L1 i L2 s kratkim žarištnim daljinama stvaraju u dva stepena izpod L2 vrlo umanjenu sliku točkastog vrha užarene katode K pomoću uzkog mlaza elektrona velike brzine. Promjer ove umanjene slike reda je 10-5 mm. Anoda visoke napetosti na slici uzki je otvor, drugi po redu, odmah izpod katode. U malenoj daljini a izpod elektronske sonde nalazi se mikroskopski objekt. Elektroni, koji prodru kroza nj, gibaju se pravocrtno u daljem prostoru do kraja cievi, jer je taj prostor bez električkog polja. Kako je broj takvih elektrona različit za različita mikropodručja objekta, i to zbog nejednakih gubitaka refleksijom i razpršavanjem, nastaje u daljini b od sonde na fluorescentnom zastoru LS ili na fotografskoj ploči F vrlo povećana sjena prosijanog diela objekta s pojedinostima njegove mikrostrukture. Povećanje je dano omjerom b/a. U sl. 4 prikazana je snimka diela jedne diatomeje dobivena ovakvim nadmikroskopom (povećanje 4200×). Snimke se odlikuju velikom dubinskom oštrinom. Raztvorna moć ograničena je s jedne strane sfernom aberacijom leća L1 i L2, s druge strane elektronskim ogibom Fresnelove vrste; u nekim je snimkama snižena do na 25 mμ. Područje primjene ovog nadmikroskopa podudara se s područjem nadmikroskopa opisanog pod 5.
 Sl. 5. Mikrokristali cinkova oksida snimljeni
Sl. 5. Mikrokristali cinkova oksida snimljeni
nadmikroskopom s rešetastim oslikavanjem.
Povećanje 8000x. Snimka od M. v. Ardennea3. Nadmikroskop s rešetastim oslikavanjem (M. Ardenne, 1938) pripada ovamo samo po upotrebljenoj elektronskoj optici, dok se sama povećana slika dobiva napola mehaničkim putem. Glavni dio Ardenneova elektronskooptičkog postupka isti je kao kod Boerschova nadmikroskopa; t. j. i on stvara elektronsku sondu s promjerom reda 10-5 mm pomoću dviju elektronskih leća kratke žarištne daljine. Ali kod njega elektronska sonda pada u sam mikroskopski objekt. Fotografska ploča dolazi neposredno iza objekta zastrta zaslonom, u kojem je u osi elektronskog mlaza uzak okrugli otvor za elektrone, koji su prodrli kroz objekt. Sonda nije nepomična, nego se pomoćnim odklonskim poljima pomiče po objektu, koji je reda veličine 10-2×10-2 mm2, redak po redak u razmacima oko 10-4 mm — slično kao u televizijskim uređajima — dok se fotografska ploča pomiče sinkrono pod objektom. Na taj je način povećanje određeno brzinom pomicanja ploče. Sl. 5 prikazuje dio jedne snimke dobivene ovim postupkom (mikrokristali cinkova oksida, povećanje 8000×). Raztvorna je moć manja u smjeru okomitom na redke nego u smjeru redaka.
4. Emisijski mikroskop je najstarija vrst e-og m-a (E. Brüche i H. Johannson, 1932). Njime se dobiva povećana slika emisije elektrona iz katode pomoću njih samih, pošto im je visoka napetost dala potrebnu veliku brzinu. No ovaj je mikroskop zbog tehničkih potežkoća oduže vrieme zaostajao povećanjima za drugim mikroskopima, koji su se razvili poslije njega; istom 1941 uspielo ga je usavršiti do nadmikroskopa (Mecklenburg). Elektronsko-optički je uređaj jednostavan: jednom elektronskom lećom (magnetskom ili elektrostatskom) stvori se povećana slika diela katode, a ova se slika drugom elektronskom lećom povećano projicira. Prema postupku, kako se izaziva emisija elektrona iz katode, diele se variante ovog mikroskopa kao i zadatci i područja iztraživanja pomoću njega:
a) Emisija elektrona izazvana je žarenjem katode;
b) osvjetljivanjem katode ultraljubičastom ili rentgenskom svjetlošću izaziva se fotoelektrički efekt; tako oslobođeni elektroni upotrebljavaju se za oslikavanje katode;
c) elektroni iz pomoćne užarene katode, koja je postrance od osi mikroskopa, ubrzani pomoćnom napetošću, udaraju u objekt smješten u osi mikroskopa kao njegova katoda. Slika objekta dobiva se u mikroskopu pomoću elektrona, koji se kod toga elastički odbiju od objekta.
Postupkom pod a) iztražuju se pojavi kod emisije elektrona iz užarenih katoda. Ako se u postupku pod b) upotrebi za katodu fotoelektrička katoda bez pogrješaka, pa se na nju projicira jedna umanjena svjetlostna slika, dobiva se e-im m-om ta slika povećana.
 Sl. 6. Prielaz željeza iz modifikacije
Sl. 6. Prielaz željeza iz modifikacije
β u modifikaciju γ. Povećanje 55x.
Snimka od Brüchea i KnechtaPostupak pod c) bio je prvobitno određen za iztraživanje kovnih površina u metalurgiji; čak i shema odgovara shemi metalurgijskog svjetlostnog mikroskopa. Ali je ovaj postupak postepeno iztisnut s jedne strane primjenom postupaka a i b na ovakva iztraživanja, a s druge strane metodom odtisaka, o kojoj će biti govora kod mikroskopa opisanog pod 5. Prevuče li se iztraživana ravna kovna površina kao katoda mikroskopa atomarnim slojem druge kovine, koja ima malenu izlaznu radnju, pa se žarenjem ili fotoelektričkim putem izazove emisija elektrona iz nje, daje emisijski mikroskop sliku površine s njezinom kristalitnom strukturom, jer se različita područja kristalita iztiču kontrastima zbog različitih jakosti elektronske emisije. U tu se svrhu upotrebljavaju atomarni slojevi alkalnih kovina, barija ili tanke navlake barijeva azida. Ovakvim su postupkom dobivene snimke b i c u sl. 6, koje prikazuju prielaz željeza iz modifikacije β u modifikaciju γ kod temperature 906°C.
 Sl. 7. Nadmikroskop s magnetskim lećama
Sl. 7. Nadmikroskop s magnetskim lećama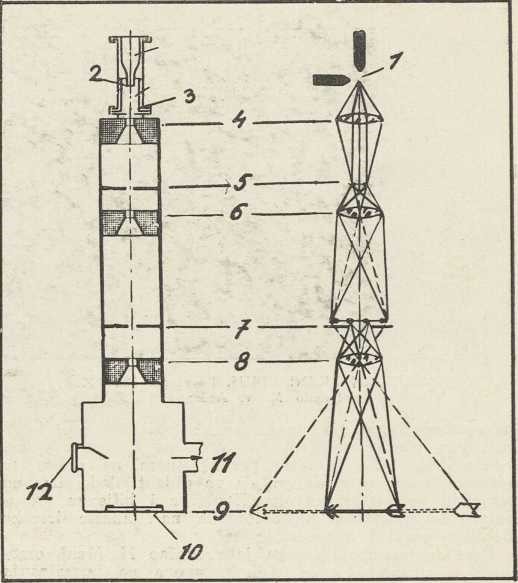 Sl. 8. Shema elektronskog nadmikroskopa uz prosijavanje objekta
Sl. 8. Shema elektronskog nadmikroskopa uz prosijavanje objekta
s ugrađenim magnetskim lećama. Uzporedba sa svjetlostnim
projekcijskim mikroskopom. Brojevi znače:
1. Izvor svjetlosti, 2 izvor elektrona (katodu),
3 anodu, 4 kondenzorsku leću,
5 ravninu objekta, 6 objektiv,
7 ravninu međuslike, 8 projekcijsku leću,
9 ravninu konačne slike, 10 fluorescentni zastor,
11 spoj sa sisaljkom, 12 prozorčić za promatranje. Sl. 9. Elektronski nadmikroskop
Sl. 9. Elektronski nadmikroskop
s elektrostatskim lećama
5. Nadmikroskop uz prosijavanje objekta elektronima podpuno odgovara postupkom i optikom normalnom dvostepenom svjetlostnom mikroskopu udešenom za projekciju ili za snimanje mikroobjekta. Najvažniji je od svih e-ih m-a, jer ima najšire područje primjene. Kad se govori o e-om m-u, obično se misli na nj. Prvi takav e. m. izradili su M. Knoll i E. Ruska 1932, a usavršili su ga na stupanj nadmikroskopa Ruska i B. Borries 1934. Prvi mikroskopi i nadmikroskopi ove vrsti radili su magnetskim lećama, dok nije H. Mahl (1939) izradio i nadmikroskop s elektrostatskim lećama. Sl. 7 prikazuje vanjski izgled nadmikroskopa s magnetskim lećama ugrađenima u cievi. U slici 8 lievo je prikazana shema istog nadmikroskopa, dok desna shema prikazuje za poredbu svjetlostni projekcijski mikroskop s prosijavanjem objekta. Uzki mlaz elektrona iz užarene katode, ograničen otvorom u anodi, dobiva veliku jednaku i stalnu brzinu od stalne visoke jednake napetosti stavljene između katode i anode. Kondenzorska uzvojnica koncentrira elektrone na objektu; pomoću elektrona, koji su prošli kroz objekt, stvara objektna uzvojnica (objektiv) u međuravnini povećanu sliku objekta, a dio ove slike projicira projekcijska uzvojnica u ravninu glavne slike. Svaka od ovih leća daje povećanje reda veličine 100×; prema tome konačno povećanje ima red veličine 10 000×. Konačna slika pada ili na fluorescentni zastor, na kojem se može promatrati kroz postrani prozorčić, ili se projicira na fotografsku ploču, pošto je postignuta najbolja oštrina. Postrani prozorčići kod međuravnine služe za promatranje međuslike na pomoćnom prstenastom fluorescentnom zastoriću, da bi se za snimku u konačnoj slici dalo odabrati zanimljivije mjesto na objektu. Prema formuli za f magnetske leće oštrina se slike može namjestiti ili finim promjenama anodne napetosti ili finim promjenama jakosti struje u uzvojnicama (→ elektronska optika); istodobno se i objekt dade mikrometrički pomicati. — Kod nadmikroskopa ove vrsti s elektrostatskom optikom anoda je izrađena tako, da djeluje kao kondenzorska leća. Sl. 9 prikazuje vanjski izgled takvog nadmikroskopa u izvedbi AEG-a. Tri vertikalna držka, završena kuglama, služe za smještanje objekta u točan položaj pred objektivom.
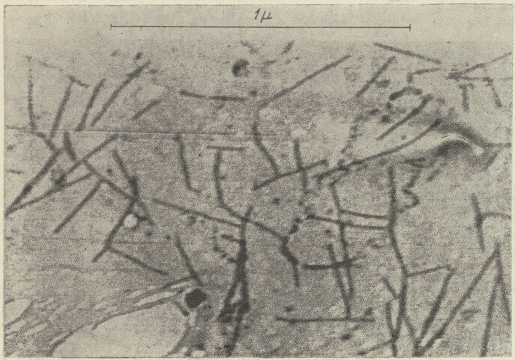 Sl. 10. Jedan biljni virus. Povećanje 50 000x.
Sl. 10. Jedan biljni virus. Povećanje 50 000x.
Snimio M. v. ArdenneOvaj je nadmikroskop već otvorio široka nova područja iztraživanja i primjena, možda manje u čisto fizikalnim pitanjima, ali to više u kemiji (struktura koloidnih čestica, celuloze, škroba i dr.), zoologiji, medicini i bakteriologiji. Njime su prvi put učinjeni vidljivima bakteriofagi, a u mnogo slučajeva i virusi (sl. 10). U pojedinim slučajevima učinjeni su vidljivima makromolekuli sa srednjim promjerom 8 mμ (molekul edestina). Preparat, koji se iztražuje, a tako i njegova podloga, moraju biti izvanredno tanki, da ne bi izazvali preveliko razpršavanje elektrona, koje bi, osim duge ekspozicije, prouzročilo i manju oštrinu slike. Za podloge se upotrebljavaju vrlo tanke kožice (nekoliko mμ) kolodija bez vlastite strukture. Ovakva se kožica s preparatom jednolično razastre preko otvora na držku za objekte; rjeđi su slučajevi, da se objekt dade izravno smjestiti na samom otvoru. Zooložke i biljevne preparate režu specialnim mikrotomima na klinaste izrezke debljine izpod 1 mikrona.
Poseban postupak, što ga je pronašao H. Mahl, omogućio je primjenu ovog nadmikroskopa na iztraživanja makroskopski ravnih površina kovina i slitina u metalurgiji; time je u mnogo pitanja iztisnuto iztraživanje takvih površina variantama a, b i c kod emisijskog mikroskopa. Taj se postupak sastoji u tome, da se napravi vrlo tanak jednoličan odtisak kovne površine, koja je na pr. kemičkim postupkom lako ojedena, pa se ovaj odtisak iztraži ovim nadmikroskopom. Kod aluminija i njegovih slitina napravimo termičkim putem tanku jednoličnu kožicu oksida, pa ovu odljuštimo elektrolitičkim putem. Kod drugih kovina radi se tako, da na površinu spustimo kap razrieđene raztopine zapon-laka pa dobivenu suhu kožicu odljuštimo elektrolizom. Ovako dobivene tanke kožice u prosijavanju elektronima pokazuju sve mikroskopske neravnosti kovne površine zbog mjestimičnih sitnih razlika u debljini.
Nekoliko snimaka iz različitih područja iztraživanja, koje su dobivene nadmikroskopima ove vrsti, prikazano je u slikama na tablama: Elektronski mikroskop I, II.
LIT.: H. Busch i E. Brüche, Beiträge zur Elektronenoptik, Leipzig 1937; M. v. Ardenne, Elektronen-Übermikroskopie, Berlin 1940; C. Ramsauer, Elektronenmikroskopie, Berlin 1942 (AEG).M. K.
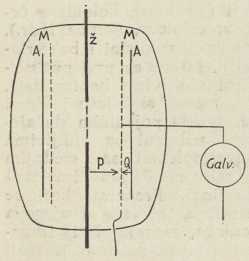 Sl. 1.
Sl. 1.Elektronski udarac je sraz, koji nastaje, kada elektron udari u atom ili molekulu. Obilna je prilika za proučavanje toga pojava, budući da se brzina tlektrona dade po volji mienjati. Jednostavan eksperimentalni uređaj za tu svrhu prikazan je u sl. 1. Vakuum-ciev s razrieđenim plinom, slična triodi (→ elektronska ciev), ima tri platinene elektrode: 1. valjkasti list A, u slici prikazan samo s dvie izvodnice, 2. u njemu valjkastu istoosnu (koaksialnu) mrežicu M i 3. u osi tih valjaka žicu Ž, kojoj je srednji dio tanak (razmak ŽM = 4 cm, MA = 1—2 mm). Električkom strujom tanki se dio žice užaruje te pušta iz sebe elektrone. Posebnom baterijom s odpornikom učini se M pozitivno električkim prema Ž, te M privlači elektrone, koji su emitirani iz Ž. Napetost P, koja vlada između M i Ž te pospješuje elektrone, može se mienjati. Jedan treći izvor struje stvara napetost između M i A, te je A slabo negativno električko prema M. Ta napetost Q ponešto zaustavlja elektrone, koji su prošli kroz oka mrežice, tako da prespori elektroni ne stizavaju do A niti teku kroz galvanometar, koji je metnut izpred A.
| km/sek |
volt |
| 100 |
0.0284 |
| 1000 |
2.84 |
| 10000 |
284 |
| 100000 |
31000 |