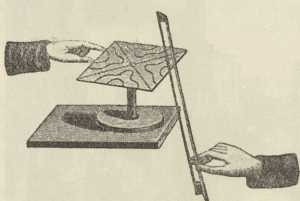
 Sl. 1. Postanak pješčane slike,
Sl. 1. Postanak pješčane slike,
uzbuđenje gudalomCHLADNI, Ernst Florens Friedrich, * Wittenberg 30. XI. 1756, † Breslau 4. IV. 1827, njemački fizičar. Svršivši pravne nauke posvetio se proučavanju akustičkih problema i glazbi. Nasuprot mišljenju svojih suvremenika C. je prvi dokazivao kozmičko porijeklo meteora. Poznate pješčane slike na pločama opisao je g. 1787 i izvađao ih na mnogim »akustičkim predstavama« u Njemačkoj, Francuskoj i Italiji. Uzdržavao se od prihoda takvih predstava i predavanja nastupajući i kao umjetnik s glazbalima, koje je sam izumio. Njegovi se pokusi izvode tako, da se gudalom (v. sl. 1.) ili udarcima uzbude vlastiti titraji ploča ili membrana, koje su pijeskom posute i zgodno učvršćene. Na čvornim se crtama pijesak sakuplja, a na ostalim ga mjestima ploča izbacuje. Titranje membrana brzoglasne slušalice, zvučnika, mikrofona s kondenzatorom može se istraživati i s pomoću ove metode. Na sl. 2. fotografirane su pješčane figure na okrugloj, duž ruba učvršćenoj ploči, kako ih je dobio američki akustičar D. C. Miller. — Backhaus je s pomoću ove metode ispitivao titranje kućice gusala (sl. 3). Chladnijeve slike se mogu načiniti i na pločicama, koje su isječene iz nekih ledaca (kremena, turmalina). U visokofrekventnom električnom polju, radi piezoelektričnog djelovanja, mijenja ovakva pločica debljinu i oblik, t. j. titra s frekvencijom polja. Pospe li se likopodijevim prahom, nastaju na njoj Chladnijeve slike, ako je frekvencija polja jedna a kojoj vlastitoj frekvenciji pločice. Slike 4 a, b, c, d pokazuju snimke ovog pojava na neučvršćenoj kvarcovoj pločici, koja ima dimenzije 30 X 30 X 8 mm i koja je iz ledca izrezana smjerom optičke osi. Kod ovih pokusa smjer električnog polja podudarao se sa smjerom optičke osi. Frekvencije pločice bile su redom: 130.000 (4a), 205.000 (b), 187.000 (c), 254.000 (d) titraja u sek. U slijedećim slikama 4e, f, g snimljeni su Chladnijevi likovi na kvarcovim pločicama, koje su brušene okomito na optičku os. Električno polje djelovalo je smjerom širine pločica. Frekvencije su bile: 134.000 (4e), 227.000 (f), 273.000 (g) titraja u sek. — Teorija titranja ploča težak je matematički zadatak. Integracija diferencijalne jednadžbe, koja ovdje dolazi, uspjela je za ploče, koje imaju oblik kruga, kvadrata, pravokutnika, romba, trokuta i elipse. D. P-ć.
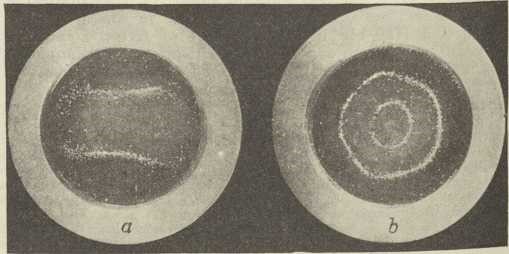 Sl. 2. Pješčane slike na okrugloj ploči
Sl. 2. Pješčane slike na okrugloj ploči
(po D. C. Milleru); frekvencije: 977 (a), 2460 (b) Sl. 3. Chladnijeva slika na guslama i frelvencija 690
Sl. 3. Chladnijeva slika na guslama i frelvencija 690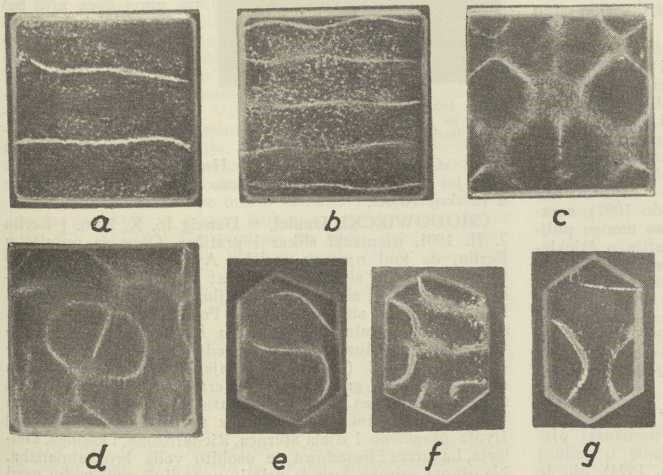 Sl. 4. Chladnijevi likovi na pločicama od kvarca
Sl. 4. Chladnijevi likovi na pločicama od kvarca
(pokusi i snimke D. Pejnovića 1935)