DVOLOM. Pojavi dvoloma opažaju se u optički anizotropnim tjelesima. Optička anizotropija sastoji se u tom, da brzina prostiranja svjetlosti zavisi o ravnini, u kojoj ona u takvom tielu titra, i o pravcu njezina prostiranja kroz tielo. Prirodno optički anizotropna tjelesa su kristali svih kristalnih sustava osim regularnog (→ anizotropski minerali). Neke organske tvari pokazuju d. u ograničenom temperaturnom području iznad svog prvog tališta; to su t. zv. tekući kristali. Optičku anizotropiju možemo proizvesti u prozirnim izotropnim tjelesima mehaničkim djelovanjem te električkim i magnetskim poljima; kod toga je često uzrok d-u poredavanje čestica i molekula. Ovamo pripadaju: d. natezanjem, tlačenjem ili savijanjem izotropnih čvrstih tjelesa; d. od strujanja (Maxwellov efekt) u viskoznim homogenim tekućinama te u nekim suspenzijama i koloidnim raztopinama; akustički d.; električki d. (Kerrov elektrooptički efekt); magnetički d. (Cotton-Moutonov efekt, Majoranin efekt, Voigtov efekt). Pribrojimo li d-u u širem smislu i cirkularni d. uzduž optičke osi kod kristala, koji zakreću ravninu polarizacije (v.), onda od d-a ne bi bio posve izuzet ni regularni kristalni sustav, jer neki kristali ovog sustava pokazuju zakretanje ravnine polarizacije u svim pravcima prolaza svjetlosti kroz njih. Cirkularni d. nije obrađen u ovom članku.
1. Dvolom u kristalima odkrio je Erasmus Bartholinus (1669) na islandskom dvolomcu. Nekoliko godina kasnije (1678) Huygens je upodpunio opažanja na dvolomcu i postavio optičku anizotropiju kao temeljnu hipotezu, na osnovu koje je mogao protumačiti glavni dio svojih opažanja. Obćenito objašnjenje za d. u kristalima dao je u prvoj četvrtini prošlog vieka Fresnel na osnovu elastične teorije svjetlosti. Prema načinu d-a dielimo dvolomne kristale u jednoosne i dvoosne. Promatrat ćemo samo pojave u prozirnim bezbojnim kristalima. U obojenim kristalima nastaju dihroizam i pleohroizam (→ dihroizam).
a) JEDNOOSNI KRISTALI. Amo pripadaju svi kristali kvadratnog i heksagonskog sustava. Od njih je najpoznatiji islandski dvolomac (kalcit). Pravac u jednoosnom kristalu, položen kroz točku upadanja svjetlosti paralelno s kristalografskom glavnom osi, zove se njegovom optičkom osi. Ravnina, položena kroz optičku os i kroz normalu upadanja, zove se glavnim presjekom kristala.
Zraka prirodne svjetlosti, koja prolazi kroz jednoosni kristal u pravcu, koji se ne podudara s optičkom osi ciepa se u dvie zrake, koje u slučaju posve prozirnih bezbojnih kristala imaju jednake intenzitete. Jedna lomljena zraka vlada se po običnom zakonu loma (redovna zraka r). Druga lomljena zraka (izvanredna, i) ne pokorava se običnom zakonu loma, jer obćenito ne leži u ravnini upadanja. Ona se lomi tako, da ostaje u ravnini glavnog presjeka. U pogledu njezina odklona u toj ravnini pokazuje se još jedna pravilnost: u t. zv. negativnim jednoosnim kristalima (na pr. kalcit) izvanredna zraka lomi se tako, da je kut između nje i optičke osi veći od kuta između upadne zrake i optičke osi; obrnuto je u t. zv. pozitivnim jednoosnim kristalima. Zbog toga se i kod okomitog upadanja svjetlosti na plohu kristala izvanredna zraka odklanja iz pravca okomice upadanja. Rezultat ovih svojstava izvanredne zrake očituje se u ovom pokusu: ako uzak svežanj svjetlosti upada okomito na plohu islandskog dvolomca, pa dvolomac okrećemo oko upadne zrake, jedna od dviju svietlih točaka na zastoru iza dvolomca ostaje kod vrtnje nepomična; ona pripada redovnoj zraci. Druga svietla točka, koja odgovara izvanrednoj zraci, okreće se kod vrtnje dvolomca u krugu oko nepomične točke. — Ako svjetlost pošaljemo kroz jednoosni kristal u pravcu njegove optičke osi, nema d-a, t. j. jednoosni kristali su u pravcu optičke osi optički izotropni.
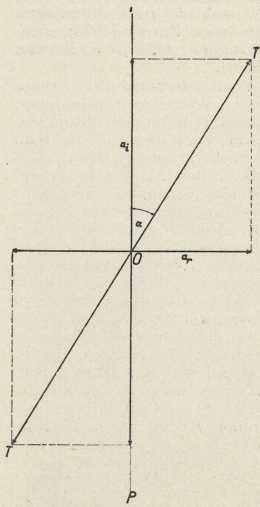
Ako kroz dvolomni kristal pošaljemo ravno polarizovanu svjetlost (jakost j), jakosti svjetlosti redovne i izvanredne zrake obćenito su nejednake, jer zavise o kutu α, koji ravnina titranja upadne svjetlosti zatvara s ravninom glavnog presjeka. Tragovi su ovih ravnina u sl. 1 označeni sa TT i sa PP. Amplitudu titranja ai svjetlosti izvanredne zrake dobit ćemo ortogonalnom projekcijom amplitude OT upadne svjetlosti na glavni presjek PP, a amplitudu titranja ar svjetlosti redovne zrake ortogonalnom projekcijom amplitude OT na ravninu okomitu na glavni presjek. Jakosti svjetlosti redovne i izvanredne zrake dane su onda Malusovim zakonom (1810):
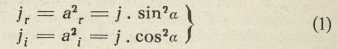
 Sl. 1.
Sl. 1.Huygensov pokus. Dva kristala islandskog dvolomca namjestimo jedan za drugim tako, da su im po dvie analogne granične plohe okomite na pravac upadne svjetlosti; Θ neka je kut među ravninama njihovih glavnih presjeka. Drugi kristal neka je učvršćen u napravi za vrtnju, s pomoću koje ga možemo obrtati oko pravca upadne svjetlosti. Na prvi kristal neka upada u uzkom okruglom svežnju prirodna svjetlost jakosti j. U put svjetlosti uključimo i jednu sabirnu leću, koja na zastoru daje oštru sliku okruglog otvora, kroz koji smo propustili svjetlost. Obćenito se i redovita (r) i izvanredna (i) zraka iz prvog kristala u drugom kristalu ciepa ju u redovitu (rr, ri) i u izvanrednu (ir, ii) zraku, pa na zastoru iza drugog kristala dobivamo obćenito četiri slike okruglog otvora. Vrtnjom ovoga kristala razabiremo, koje od ovih slika pripadaju zrakama ir i ii, jer se one vrte s kristalom, dok slike, koje pripadaju svjetlosti zraka rr i ri, ostaju kod vrtnje nepomične. Svjetlostni intenziteti ovih četiriju slika obćenito su nejednaki, jer zavise o kutu Θ među glavnim presjecima. Samo za Θ = (2n ± 1) • 45° sve četiri slike imaju jednake intenzitete. Za Θ = 0° i 180° izčezne par slika ri i ir, a za Θ = 90° i 270° izčezne par rr i ii.
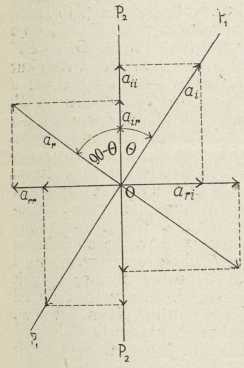
Redovita i izvanredna zraka su ravno polarizovane. U dvolomcu postoje za svaki smjer prostiranja svjetlosti samo dvie međusobno okomite ravnine, u kojima svjetlost može titrati: to su ravnina glavnog presjeka i ravnina položena kroz zraku okomito na ravninu glavnog presjeka. To je glavni zaključak u tumačenju Huygensova pokusa, koji je, uz transverzalnost titranja, izveo Fresnel (1821) iz svog i Aragoova nalaza iz g. 1816, da svjetlost redovite i izvanredne zrake ne mogu međusobno interferirati. Prirodna svjetlost, koja upada na kristal, dieli se u njemu u dva jednaka ravno polarizovana diela, od kojih jedan (izvanredna zraka i) titra u ravnini glavnog presjeka, a drugi dio (redovita zraka r) titra u ravnini okomitoj na glavni presjek. Svaka od ovih zraka ciepa se u drugom kristalu po Malusovu zakonu (1), pa primjenom ovog zakona dobivamo za jakosti svjetlosti u zrakama rr, ri, ir, ii ove izraze (sl. 2; P1P1, P2P2 su tragovi glavnog presjeka prvog, odnosno drugog dvolomca):
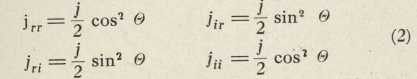
 Sl. 2.
Sl. 2.Kod Θ = 0° i zraka r i zraka i iz prvog kristala nastavljaju svoj put u drugom kristalu kao redovita i kao izvanredna zraka; oba se kristala vladaju kao jedan, pa je razmak među slikama rr i ii na zastoru proporcionalan ukupnoj debljini. Slično je kod Θ = 180°; samo se u ovom slučaju zraka i kao ii u drugom kristalu lomi na suprotnu stranu, pa na izlazu iz drugog kristala, ako oba kristala imaju jednake debljine, zrake rr i ii padaju zajedno i daju jednu sliku otvora (jakost j). Za Θ = 90° i Θ = 270° redovita zraka r iz prvog kristala prolazi kroz drugi kristal kao izvanredna zraka (ir), a izvanredna zraka i prolazi kroz drugi kristal kao redovita zraka (ri).
Lom pojedinih zraka, kako je ovdje protumačen, temelji se na prvom osnovnom svojstvu jednoosnih kristala, koje je upoznao već Huygens. Razlike u lomu redovne i izvanredne zrake u islandskom dvolomcu stoje po Huygensu u tome, što se svjetlost redovite zrake prostire kroz kristal u svim smjerovima istom brzinom, dok brzina prostiranja svjetlosti izvanredne zrake zavisi o kutu među pravcem prostiranja i optičkom osi. Konstrukcijom elementarnih valova za svjetlost redovne i izvanredne zrake dobivamo dvojake valne plohe: kuglu za svjetlost redovne zrake, rotacioni elipsoid za svjetlost izvanredne zrake. U pravcu optičke osi svjetlost redovne i izvanredne zrake prostiru se istim brzinama, pa se kugla i rotacioni elipsoid u pravcu optičke osi dodiruju. Kod nekih jednoosnih kristala brzine prostiranja izvanredne zrake u pravcima izvan optičke osi manje su od brzine prostiranja redovne zrake; dakle je kod njih rotacioni elipsoid upisan u kugli. To su pozitivni jednoosni kristali; takvi su kalomel, kvarc, led, rutil i dr. Veću skupinu čine jednoosni kristali, u kojima su brzine prostiranja izvanredne zrake u smjerovima izvan optičke osi veće od brzine prostiranja redovne zrake, tako da je u njima elementarna kugla upisana u elementarnom rotacionom elipsoidu. Takvi su kristali negativno jednoosni; ovakvi su: kalcit (islandski dvolomac), apatit, korund, natrijeva salitra i dr.
Najveću razliku među brzinama obiju zraka imamo u pravcu okomitom na optičku os. Brzina redovite zrake (νr) i brzina izvanredne zrake (νi) u ovom pravcu zovu se glavnim brzinama svjetlosti u kristalu. To su ujedno ekstremne vriednosti brzine svjetlosti izvanredne zrake. Prema tome je u pozitivnim jednoosnim kristalima νi a u negativnim νi>vr.
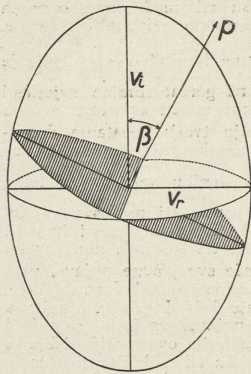 Sl. 3.
Sl. 3.Mjesto Huygensovom dvoslojnom valnom plohom mogu se brzine obiju zraka za različite kutove prema optičkoj osi prikazati Fresnelovim elipsoidom brzina za jednoosne kristale. To je rotacioni elipsoid, u kome se os rotacije podudara s kristalografskom osi kristala; glavna poluos učinjena mu je proporcionalnom sa νi, a sporedna poluos proporcionalnom sa vr. Prema tome je Fresnelov elipsoid produžen kod negativnih, a splošten kod pozitivnih jednoosnih kristala. Da bismo iz Fresnelova elipsoida odredili brzinu izvanredne zrake za smjer p, definiran kutom β prema optičkoj osi, presiečemo elipsoid diametralnim presjekom okomitim na p (sl. 3, za negativni kristal). Onda je brzina izvanredne zrake za smjer p predočena na ovoj presječnoj elipsi njezinom poluosi, koja leži izvan ekvatora elipsoida, dok poluos u ravnini ekvatora predstavlja konstantnu brzinu vr.
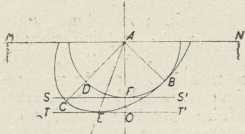 Sl. 4.
Sl. 4.U sl. 4 prikazan je dvolom ravnog vala svjetlosti, koji upada paralelno na graničnu plohu MN jednoosnog negativnog kristala; ravnina crtnje je glavni presjek kristala, AB je njegova optička os. Za vremenski razmak Δt valna je ploha redovne zrake kugla sa središtem u A; njezin trag u ravnini glavnog presjeka je krug BFD. Valna je ploha izvanredne zrake za isti vremenski razmak rotacioni elipsoid prikazan u ravnini glavnog presjeka elipsom BEC. Fronta ravnog vala, koji odgovara redovnoj zraci, za trenutak Δt je tangencialna ravnina SS1 kugle s diralištem u F, a fronta ravnog vala, koja odgovara izvanrednoj zraci, tangencialna je ravnina TT1 elipsoida s diralištem u E. Uzmemo li Δt za jedinicu vremena, AF je brzina svjetlosti redovne zrake u pravcu zrake, AE je brzina svjetlosti izvanredne zrake u pravcu zrake. Kod redovne zrake je brzina svjetlosti AF brzina širenja vala svjetlosti (valna brzina), jer je AF normala na valnu frontu SS1. Za izvanrednu je zraku valna brzina svjetlosti AO, jer je AO normala na valnu frontu TT1 izvanredne zrake; ona se obćenito razlikuje od brzine u smjeru zrake. Samo za glavne brzine vr i vi valna brzina svjetlosti izvanredne zrake podudara se s brzinom u smjeru zrake.
Pomoću valne brzine definira se indeks loma izvanredne zrake za dani smjer širenja ovako:
n’ = brzina svjetlosti u vakuumu / valna brzina u kristalu
Njegove su ekstremne vriednosti: nr=c/νr, gdje je nr ujedno indeks loma za redovnu zraku. U islandskom je dvolomcu za žutu natrijevu crtu: nr = 1,6584, ni = 1,4864.
Analogno Fresnelovu rotacionom elipsoidu za brzine u smjeru zraka može se konstruirati i indeksni elipsoid. To je rotacioni elipsoid, komu je ni; poluos vrtnje, koja ujedno pada u kristalografsku os, dok mu je nr ekvatorialni polumjer. Prema tome on je splošten kod negativnih, a produžen kod pozitivnih jednoosnih kristala. Iz njega se mogu konstrukcijom izvesti valne brzine svjetlosti izvanredne zrake: za dani smjer p valna je brzina proporcionalna s recipročnom vriednosti glavne poluosi presječne elipse, u kojoj diametralna ravnina, okomita na p, sieče indeksni elipsoid, računajući kao glavnu poluos onu, koja leži izvan ravnine ekvatora; valna brzina redovne zrake konstantno je jednaka recipročnoj vriednosti ekvatorialnog polumjera.
b) DVOOSNI KRISTALI (Brewster, 1815). U kristalima rombičkog, monoklinskog i triklinskog sustava pojavi su d-a mnogo zamršeniji, jer se obje zrake, u koje se u kristalu ciepa upadna zraka, obćenito vladaju kao izvanredne zrake. Samo u tri određene, međusobno okomite ravnine jedna se zraka vlada kao redovna zraka jednoosnih kristala.
Prvu suvislu teoriju d-a u dvoosnim kristalima, ujedno obću teoriju d-a, u koju ulaze jednoosni kristali kao jednostavniji slučaj, dao je Fresnel u nizu radnja od g. 1821 do 1827. Fresnelova teorija svodi d. na elastičnu anizotropiju etera u kristalima: elastičnost etera, koja uz njegovu gustoću u elastičnoj teoriji svjetlosti određuje brzinu svjetlosti u tvari, u optički anizotropnim tjelesima zavisi o položaju pravca širenja svjetlosti prema određenim iztaknutim pravcima u tielu. To su tri međusobno okomita pravca, kojima odgovaraju tri glavne vriednosti e1, e2, e3 elastičnosti etera, a ovima prema formuli:
v=√e/d,
gdje jed gustoća etera, odgovaraju tri glavne brzine svjetlosti v1, v2 v3. U elektromagnetskoj teoriji svjetlosti sveden je d. na električnu anizotropiju tvari: konstanta dielektričnosti u jednom pravcu u kristalu, koja prema Maxwellovoj relaciji: v = c/√ε određuje brzinu svjetlosti u tvari, zavisi o položaju tog pravca prema tri međusobno okomita pravca, u kojima konstanta dielektričnosti ima tri glavne vriednosti ε1, ε2, ε3. Obje teorije vode konačno na iste rezultate i izpravno tumače sve glavne pojave, ukoliko se ovi odnose na monohromatsku svjetlost. Njihova je značajka, da one promatraju kristal kao kontinuiranu tvar. Potežkoće u tumačenju pojava, zavisnih o valnoj dužini svjetlosti, na koje su nailazile ove teorije, izbjegle su novije, atomističke, teorije d-a (Ewald, Born), koje d. izvode iz građe kristala od atomskih skupina, koje tvore atomsku mrežu kristala.
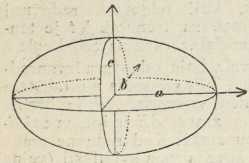 Sl. 5.
Sl. 5.Kod dvoosnih kristala ulogu Fresnelova rotacionog elipsoida zauzima Fresnelov troosni elipsoid, kojemu poluosi predočuju tri glavne brzine svjetlosti v1, v2, v3 (sl. 5). Brzine zraka za dani pravac p nalazimo i ovdje po pravilu, da su one jednake poluosima elipse, dobivene diametralnim presjekom elipsoida ravninom položenom okomito na p. Odatle izvodimo oblik valovne plohe zraka za dvoosne kristale.
Neka su glavne brzine svjetlosti v1 = a, v2 = b, v3= c, te neka je a>b>c. Brzine zraka za zrake u ravnini glavnih brzina ac (xz) nalazimo primjenom gornjeg pravila. Za smjer p, koji pada u pravac x, imamo u sl. 5 okomitu presječnu elipsu s poluosima b i c. To su brzine zraka u pravcu x. Za pravac p≡z nalazimo u sl. 5 vodoravnu presječnu elipsu s poluosima b i a.To su brzine zraka u pravcu z. Za ma koji drugi položaj pravca p u ravnini xz dobivamo presječnu elipsu, kojoj je jedna poluos uviek b, a druga poluos ima neku vriednost između a i c. Tako dobivamo kao presjek valovne plohe zraka s ravninom xz krug s polumjerom b simetrično presječen elipsom s poluosima a i c (sl. 6). Analogno dobivamo presjeke valovne plohe zraka s ravninama ab ≡xy i bc≡yz. Za pravac p≡y dobivamo presječnu elipsu s poluosima a i c, a za p≡x elipsu s poluosima b i c kao gore. Za sve druge položaje pravca p u ravnini xy imamo elipse, kojima je jedna poluos c, a druga ima vriednost između a i b. Dakle presjek valovne plohe zraka s ravninom xy sastoji se od elipse s poluosima a i b i u njoj koncentričnog kruga s polumjerom c (sl. 7). Napokon kao presjek valovne plohe zraka s ravninom yz izlazi krug s polumjerom a i u njemu koncentrična elipsa s poluosima b i c (sl. 8). Perspektivnu predočbu o valovnoj plohi zraka daje sl. 9, u kojoj su prikazani njezini presjeci s tri glavne ravnine xz, xy yz.
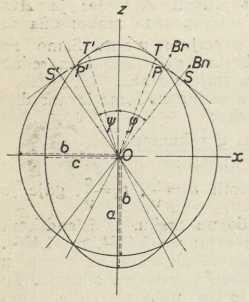 Sl. 6.
Sl. 6.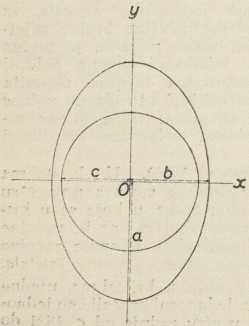 Sl. 7.
Sl. 7.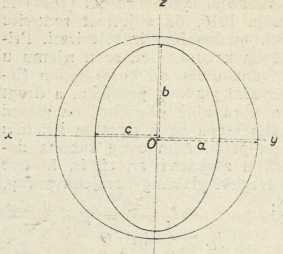 Sl. 8.
Sl. 8.Posebna važnost pripada nekim točkama i pravcima u ravnini xz. U točki P (sl. 6) sieku se elipsa i krug; to znači, da se u pravcu OP (kao i u analognom pravcu OP’) obje zrake u kristalu šire istom brzinom b. Pravci OP i OP’ zovu se optičkim osima zraka ili biradialama (Br). Kao kut među njima računa se kut POP’=2ψ. — Krug i elipsa u ravnini xz imaju zajedničku tangentu TS, dotično T’S’. Prema tome je TSOS, dotično T’S’OS’; dakle su OS zajednička normala, a TS zajednička valna fronta za oba međusobno okomito polarizovana vala, koji se šire smjerovima OS i OT, t. j. oba se vala šire u kristalu istom valnom brzinom b. Pravci OS i OS’ zovu se optičkim osima dvoosnog kristala ili binormalama (Bn); one odgovaraju optičkoj osi jednoosnih kristala. Kut među njima je SOS’=2φ. Njegova simetrala (os z) zove se srednjicom dvoosnog kristala. Dvoosni kristali diele se u pozitivne i negativne prema tome, je li kut 2φ oštar ili tup; to pak zavisi o tome, da li srednja glavna brzina valova dolazi bliže najvećoj ili dolazi bliže najmanjoj glavnoj brzini. Kutovi 2φ i 2ψ gotovo se uviek malo razlikuju jedan od drugoga. Veza između njih i glavnih indeksa loma glasi:
tgφ = n3/n1tgψ, (3)
a indeksi loma prosječno se malo razlikuju jedan od drugoga. Tako te razlike među ovim kutovima iznose kod gipsa 0°18’, a kod tinjca 0°59’. Veće su razlike kod rombičkog sumpora (7°23’) i kod nekih organskih kristala. Iz formule (3) izlazi ujedno, da φ i ψ obćenito zavise i o valnoj dužini svjetlosti, jer o njoj zavise indeksi loma (disperzija optičkih osiju).
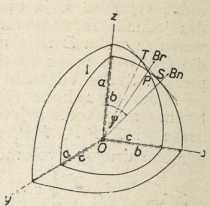 Sl. 9.
Sl. 9.Ravni val, koji se prostire u pravcu optičke osi (binormale) OS, t. j. koji napreduje paralelno s tangencialnom ravninom ST (sl. 6 i 9), ne dodiruje valnu plohu samo u točkama S i T, nego u svim točkama jednog kruga s promjerom ST, u kome tangencialna ravnina ST dodiruje valnu plohu oko njezine ljevkaste udubine kod P. Prema tome, ravnom valu ST odgovara bezbroj zraka ravno polarizovane svjetlosti, koje sačinjavaju izvodnice čunja s vrhom u O, a kojemu je baza krug s promjerom ST. Pri izlazu iz kristala u vanjsko sredstvo te se zrake lome tako, da su okomite na frontu ravnog vala, pa se dobiva šuplji cilindar zraka, koji na zastoru daje prsten svjetlosti. Promjer prstena nezavisan je o daljini zastora od kristala. Smjerovi titranja svjetlosti na pojedinim zrakama prstena upereni su prema točki S, a titraji na samoj zraci OS okomiti su na ravnini crtnje (Sl. 6). Taj je pojav nazvan unutrašnjom koničkom refrakcijom. Nju je pronašao teoretskim putem Hamilton (1832) kod proučavanja valne plohe, a iduće ju je godine dokazao Lloyd na aragonitu. Optičke osi (binormale) zovu se često i osima unutrašnje konicke refrakcije.
Svjetlosti, koja se u kristalu širi smjerom biradiale OP (sl. 6 i 9), odgovaraju u ravnini xz ravne fronte vala, koje su tangente valnih ploha u točki P. U prostoru odgovara joj bezbroj valnih fronta, koje su tangencialne ravnine obiju valnih ploha s diralištem u P, a pripadaju im različite brzine. Obrnuto, ako izvana upadaju na kristal takve tangencialne valne fronte, one se u kristalu šire smjerom biradiale kao nit zraka s različitim valnim brzinama. Na izlazu iz kristala na suprotnoj strani ove se zrake lome tako, da se svaki val prostire u smjeru svoje valne normale,pa sve zrake čine uzak čunj. Na zastoru se dobiva svietli prsten, kojemu promjer raste s daljinom zastora od kristala. Taj je pojav nazvan vanjskom koničkom refrakcijom. I nju je teoretskim putem našao Hamilton, a eksperimentalno ju je dokazao Lloyd. Biradiale se zovu i osima vanjske koničke refrakcije.
Karakter dvolomnih kristala određuje se pojavima interferencije u konvergentnoj polarizovanoj svjetlosti. Aparatura se sastoji od polarizatora i analizatora, koji se da vrtjeti, i sabirne leće između njih. Pločica kristala dolazi u konvergentni svežanj svjetlosti iza leće, a druga sabirna leća čini svjetlost paralelnom ili stvara sliku na zastoru. Za subjektivno opažanje može se upotriebiti Nörrenbergov polarizacioni aparat preinačen u tu svrhu (konoskop). Za iztraživanje malenih kristala služi polarizacioni mikroskop.
Sl. 1 na tabli: Dvolom pokazuje pojav interferencije, koji daje pločica jednoosnog kristala, izrezana okomito na optičku os, među ukrštenim nikolima u homogenoj konvergentnoj svjetlosti. U bieloj svjetlosti dobivaju se obojeni prstenovi. Kod debljih pločica prstenovi dolaze gušće jedan za drugim. Među paralelnim polarizatorima pojav je komplementaran, ukoliko crni križ prelazi u svietli, a tamni i svietli prstenovi, isto tako i svietla i tamna polja oko sredine, izmiene svoja mjesta.
Pločica jednoosnog kristala, izrezana paralelno s optičkom osi, smještena u konvergentnoj svjetlosti među ukrštenim nikolima tako, da optička os zatvara s ravninom titranja polarizovane svjetlosti kut oko 45°, daje dvostruki sustav hiperbola (sl. 2 na tabli: Dvolom).
Pločica dvoosnog kristala, izrezana okomito na njegovu srednjicu, daje u konvergentnoj svjetlosti sustav tamnih i svietlih krivulja, sličnih lemniskatama. Polovi lemniskata odgovaraju optičkim osima. Među ukrštenim polarizatorima sustav lemniskata presječen je crnim križem, kojemu jedan krak prolazi kroz polove, a drugi ide okomito kroz središte slike (sl. 3 na tabli: Dvolom). Među paralelnim polarizatorima, uz izmjenu tamnih i svietlih polja, tamni križ prieđe u svietli. Ako pločica leži tako, da trag ravnine optičkih osi zatvara kut 45° s ravninom titranja polarizovane svjetlosti, križ prieđe u dva luka hiperbole, koji prolaze kroz polove.
Pločica dvoosnog kristala, izrezana okomito na jednu od optičkih osi, daje u konvergentnoj svjetlosti sustav svietlih i tamnih krugova presječenih dvjema tamnim prugama, koje među ukrštenim polarizatorima prieđu u diametralnu tamnu prugu.
Predznak dvolomnih kristala može se odrediti s pomoću promjene u njihovoj slici interferencije u konvergentnoj polarizovanoj svjetlosti, koju proizvodi pločica jednog dvolomnog kristala istoga karaktera i poznatog predznaka brušena na analogan način. Ako se umetanjem ove pločice krivulje interferencije sužuju, obje su pločice istog predznaka, a ako se krivulje razilaze, pločice imaju protivne predznake.
Jednostavnije je odrediti predznak kristala iz promjena, koje u njegovoj slici interferencije u konvergentnoj svjetlosti izaziva umetanje jedne λ/4 -pločice u put zraka tako, da je njezina ravnina optičkih osi u azimutu 45° prema ravnini titranja polarizovane svjetlosti (Dove 1837). Sl. 4 (na tabli: Dvolom) prikazuje promjene, koje izaziva tako namještena λ/4 -pločica u slici interferencije jednoosnog kristala izrezanog okomito na optičku os: u dva suprotna kvadranta prstenovi su razmaknuti, a pojavile su se bkzu središta dvie tamne mrlje. Ako ove tamne mrlje leže u pravcu, koji odgovara tragu optičkih osi λ/4 -pločice, kristal je pozitivan; u suprotnom je slučaju negativan. Analogno se iz promjena, prouzročenih u sustavu lemniskata dvoosnog kristala, pomoću λ/4 -pločice da odrediti predznak takvog kristala.
Opažanja i mjerenja slabih d-a izvode se s pomoću pločica s osjetljivom bojom (na pr. Soleilova pločica) ili s pomoću pločica na načelu polusjene (Bravaisova, Calderonova). Pomoću Bravaisove pločice dadu se još sigurno razpoznati fazne razlike reda veličine 0,0001 • 2π.
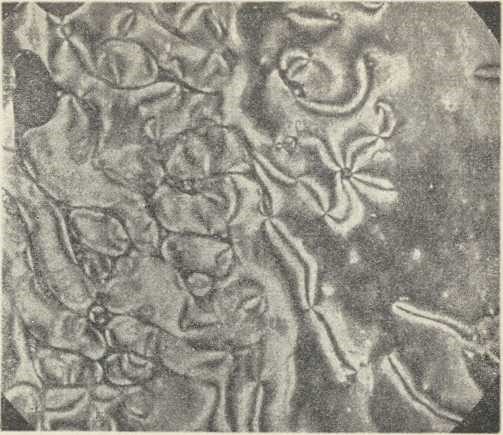 Sl. 10. p-azoksifenetol u polarizacionom mikroskopu
Sl. 10. p-azoksifenetol u polarizacionom mikroskopu
među ukrštenim nikolima
(Wien-Harms, Handbuch der Experimentalphysik,
sv. 18., Leipzig 1928)c) TEKUĆI KRISTALI. Ima cieli niz organskih kristaliničnih tvari, koje kod postepenog dizanja temperature pokazuju dva tališta: kod nižeg tališta kristal prelazi u jednu, ponajčešće mutnu tekuću fazu, koja je optički anizotropna (»mezomorfno stanje«), a kod višeg tališta ova faza prelazi u bistru, optički izotropnu tekuću fazu. Pojav je odkrio Reinitzer (1888) na holesterinu, a glavna iztraživanja izveo je O. Lehmann, koji je tomu posvetio dobar dio svog života. Od njega potječe i naziv »tekući kristali« za optički anizotropnu fazu. Međutim iztraživanja Debye-Scherrerovom metodom pokazala su, da u toj fazi nema ni traga mikropodručjima s kristaličnom strukturom (Hückel 1921). Temperaturni razmak, u kojem postoji ova faza, različit je kod različitih tvari pa ide od nekoliko °C do preko 100°C. Anizotropna faza se u pogledu viskoznosti nimalo ne iztiče prema običnim tekućinama; ima čak tvari, kod kojih je ona židkija od vode (na pr. p-azoksifenetol). Promatramo li anizotropnu fazu u polarizacionom mikroskopu (konvergentna svjetlost), pokazuju se više manje jasne slike interferencije (sl. 10). D. se pripisuje lančastoj građi molekula. Po Lehmannu on nastaje tim, što se takvi lančasti molekuli ili snopovi njih spontano poredaju u povećim područjima u prosječno iste pravce. Prema tome bi ovaj d. pripadao širem području d-a onentacijom.
2. Akcidentalni dvolom ili dvolom deformacijom. Pod tim razumievamo d., koji pokazuju homogena izotropna prozirna čvrsta tjelesa pod djelovanjem mehaničkih napetosti izazvanih tlakom, natezanjem ili torzijom. Prvi je odkrio Brewster god. 1815, da pločica želatina kod savijanja postaje dvolomna, a onda je taj pojav našao i iztražio na staklu, fluoritu, čvrstim smolama i t. d. Pokazalo se, da d. u ovakvim tvarima prouzrokuju već slabe vanjske sile. Kod toga sve tvari, koje nisu kristalinične, postaju pod djelovanjem tlaka optički jednoosne, i to većinom negativno, s optičkom osi paralelnom s pravcem djelovanja tlaka. Neke vrsti flintova stakla pokazale su u takvom slučaju pozitivnu jednoosnost.
 Sl. 11. Dvolom u štapiću trolona pod obterećenjem
Sl. 11. Dvolom u štapiću trolona pod obterećenjem
(G. Mesmer, Spannungsoptik, Berlin 1939)Iztraživanja su pokazala, da je ovakav d. u elastičnim tjelesima proporcionalan izazvanoj deformaciji do krajnje granice elastičnosti. Prema Hookeovu zakonu elastičnosti izlazi onda, da je d. proporcionalan vanjskoj sili. Na osnovu toga moguće je d-om iztražiti razpodjelu mehaničkih napetosti u deformiranom tielu, pa se to primjenjuje u fotoelastičkim iztraživanjima čvrstoće i obteretljivosti dielova građevina i strojnih dielova s pomoću d-a u modelima izrađenim iz zgodnog prozirnog izotropnog tvoriva (Mesnager 1901). Od takvog tvoriva traži se, da ima velik elasto-optički koeficient, da je što savršenije elastično, i da d. nestane bez ostataka, kad prestane djelovati vanjska sila. Tome najbolje odgovaraju staklo, neke vrsti celuloida, ksilonit i neki derivati umjetnih smola (trolon, dekorit). Iztražuje se izključivo interferencijom u paralelnoj polarizovanoj svjetlosti među ukrštenim polarizatorima (sl. 11).
Dosada nema nijedne teorije, koja bi posve osvietlila akcidentalni d. s gledišta unutrašnje strukture tvari. Prvu fenomenoložku teoriju pojava izradio je F. Neumann (1841).
Ovamo idu i liepi pojavi hromatske interferencije, koju trajno pokazuju naglo ohlađeni komadi stakla (sl. 12). Prvi ih je opažao Seebeck (1813), a izpravno ih je protumačio Brewster akcidentalnim d-om, komu je uzrok u unutrašnjim mehaničkim napetostima izazvanima nejednolikim ohlađivanjem. Isto tako kod nejednoličnog zagrijavanja stakla nastaje d. zbog nejednolike razpodjele mehaničkih napetosti.
 Sl. 12. Dvolom u naglo ohlađenoj ovalnoj staklenoj pločici
Sl. 12. Dvolom u naglo ohlađenoj ovalnoj staklenoj pločici
(Müller-Pouillets,
Lehrbuch der Physik,
2. sv., Braunschweig 1929)I optička svojstva kristala mienjaju se pod utjecajem mehaničkih sila. Kristali regularnog sustava, za razliku od drugih optički izotropnih tjelesa, postaju pod djelovanjem tlaka obćenito optički dvoosnima; međutim pod djelovanjem jednostranog tlaka u nekim određenim pravcima i oni postaju optički jednoosnima. Optički jednoosni kristali ostaju jednoosni, ako tlak djeluje paralelno s optičkom osi, a postaju dvoosnima, ako tlak djeluje okomito na optičku os. Kod dvoosnih kristala mienja se pod tlakom kut među optičkim osima.
3. Dvolom orientacijom. O. Wiener (1904) razvio je teoriju, prema kojoj je jedno tielo, složeno od homogenih i jednakih čestica, malenih prema valnoj dužini svjetlosti i poredanih izvjestnim redom u drugom homogenom sredstvu, dvolomno i onda, ako su i čestice i sredstvo po sebi optički izotropni. Predpostavka je, da se uklopljene čestice razlikuju indeksom loma od sredstva. Ako su uklopljene čestice uzporedni štapići od prilike jednakih dužina (na pr. vlakna kod nekih tvari s mikro-vlaknastom strukturom), složeno se tielo vlada kao pozitivan jednoosni kristal, koji ima optičku os u pravcu vlakana. Ako uklopljene čestice imaju oblik lamela, poredanih paralelno, složeno se tielo vlada kao negativan jednoosni kristal, kojemu optička os leži okomito na pravac lamela. Friedel je eksperimentalno potvrdio ove Wienerove zaključke. Ovamo ide d., koji pokazuju listići celofana, kao i anomalni dvolom (t. zv. lamelama polarizacija), koji se kadkada opaža na kristalima regularnog sustava, ako imaju lamelarnu strukturu (Biot 1842). Ambronn je dalje razvio ove Wienerove nazore te je pokušao primieniti ih na tumačenje akcidentalnog d-a deformacijom. Ujedno je temeljna misao ove Wienerove teorije bila putokazom u tumačenju nekih slučajeva umjetno izazvanog d-a, koji ovdje sliede.
4. Akustički dvolom. Već je Biot (1820) u vezi s Brewsterovim opažanjima o akcidentalnom d-u u staklu našao d. u uzkoj i dugoj staklenoj ploči, koju je trenjem vlažnom krpom doveo u longitudinalno titranje. Kasnije je Kundt s pomoću svog polarizacionog vibroskopa dokazao, da je kod toga d. najjači u čvorovima stojnih valova, te da se staklo u titrajnoj poluperiodi stezanja vlada kao optički negativan, a u poluperiodi raztezanja kao optički pozitivan jednoosni kristal. Nakon mnogih uzaludnih pokušaja, da se dokaže akustički d. u čvorovima stojnih zvučnih valova u tekućinama, ovakav su d. dokazali nekako istodobno Lucas i Kawamura posljednjih godina (1938) s pomoću ultrazvučnih valova. Lucas ga je našao u nekim vrlo viskoznim tekućinama (ricinusovo i laneno ulje) pod djelovanjem progresivnih ultrazvučnih valova, a Kawamura u suspenzijama vanadijeva pentoksida pod djelovanjem ultrazvučnih stojnih valova. Pojavi su dosada premalo iztraženi. Po Lucasu se akustički d. u viskoznim tekućinama ima pripisati tlakovima i natezanjima zbog gradienta polja brzina u smjeru širenja valova. Za akustički d. u suspenzijama, ukoliko bi on bio ograničen na hidrosole i hidrogele s elipsoidalnim i pločastim česticama, Oka polazi od temeljne misli orientacionog d-a. Pločaste bi se čestice u polju ultrazvučnih stojnih valova vladale kao Rayleighove (Dvořákove) pločice namještajući se u trbusima stojnih valova okomito na smjer širenja ultrazvuka.
5. Dvolom u tekućinama kod strujanja. Kod ovog d-a razlikujemo dvie skupine pojava: d. u čistim viskoznim tekućinama u strujanju (Maxwellov efekt) i d. u koloidnim raztopinama u strujanju. Zajednički je preduvjet za obje skupine taj, da među susljednim slojevima tekućine u gibanju ima postojati neprekidan pad brzina. Po starijem tumačenju ovakav je d. u čistim viskoznim tekućinama neposredna posljedica pada brzina. Zbog toga nastaju mehaničke napetosti među slojevima, pa bi s fenomenoložkoga gledišta ovakav d. pripadao među d-e deformacijom. Kod d-a koloidnih raztopina u strujanju radi se o djelomičnoj orientaciji duguljastih čestica. Po tome bi d. u raztopinama lančastih makromolekula u strujanju bio prelazno područje između ovih dviju skupina. Molekularne teorije svode i d. u čistim tekućinama u strujanju na d. orientacijom.
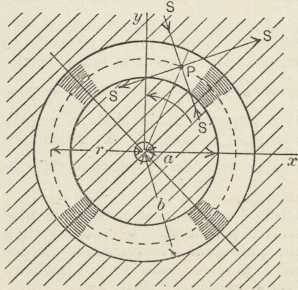 Sl. 13. Shematski prikaz uređaja
Sl. 13. Shematski prikaz uređaja
za II. Maxwellovu metoduD. kod strujanja prvi je opazio Maxwell na kanadskom balsamu (1873). Prvi veći niz iztraživanja na različitim tekućinama izveo je Kundt (1881) upotrebljavajući kod toga t. zv. II. Maxwellovu metodu, koja se i danas gotovo izključivo upotrebljava u ovakvim iztraživanjima. Uređaj se sastoji od dva koncentrična kovna valjka, od kojih se unutrašnji jednoliko vrti. Tekućina dolazi u uzki prostor između njih, pa se ona poslije postignuća stacionarnog stanja nalazi u takvom strujanju, da kutna brzina susljednih slojeva opada prema stieni mirnog valjka. Brzina vrtnje unutrašnjeg valjka mora biti tako odmjerena, da tekućina uz njegovu stienu struji laminarno. Snop ravno polarizovane svjetlosti prolazi kroz tekućinu paralelno s osi valjaka. Svaki elementarni volumen tekućine podvrgnut je zbog radialnog opadanja brzine tangencialnom natezanju, koje proizvodi njegovu deformaciju u dva međusobno okomita pravca nagnuta za 45° prema polumjeru (sl. 13). Među ukrštenim polarizatorima d. se očituje pojavom svjetlosti u određenim kutnim područjima vidnog polja, a raste proporcionalno s kutnom brzinom unutrašnjeg valjka.
Koloidne raztopine u jednakom uređaju pokazuju d., ako čestice disperzne faze imaju duguljast ili pločast oblik; tako ga pokazuju hidrosoli vanadijeva pentoksida. Djelovanje natezanja zbog pada brzine na ovakve čestice jest u tom, da one nastoje orientirati se oko trajektorije strujanja tako, da izduženi elipsoidi dođu svojom dužom osi u pravac strujanja, a pločaste čestice da se smjeste oko okomice na taj pravac. Ovakva je orientacija samo statistička, jer nasuprot poredanju djeluje Brownovo gibanje; s druge strane teorija pokazuje, da i same čestice dolaze kod strujanja u nejednoliku vrtnju. D. koloidnih raztopina u strujanju obćenito odgovara d-u jednoosnih kristala. Tumačenje eksperimentalnih rezultata često je otežčano tim, što su suspendirane čestice već po sebi optički anizotropne, ili takva anizotropija može nastati njihovom deformacijom pod djelovanjem sila u strujanju. Anomalije dolaze i od polidisperznosti suspenzija.
Pojedinačno zastupana mišljenja (Krüger, Björnståhl), da bi se d. homogenih tekućina u strujanju imao svesti na d. orientacijom prašine stranih čestica u njima, uklonjena su, kad je prašina odstranjena destilacijom tekućine u vakuumu, pa je tako očišćena tekućina u strujanju ipak pokazala d. Preduvjet je, da takva tekućina nema premalenu viskoznost. Molekularnu teoriju d-a strujanjem za čiste homogene tekućine obradili su Raman i K. S. Krishnan (1928) uz predpostavku, da molekuli takve tekućine imaju oduljen elipsoidalan oblik i da su po sebi optički anizotropni. Djelovanje pada brzine na njih izlazi na to, da molekuli u strujanju teže da se pravcem svoje duže osi nagnu za 45° prema polumjeru. Između ove težnje i suprotnog djelovanja termičkog gibanja molekula uzpostavi se konačno dinamička ravnoteža, u kojoj znatan dio molekularnih odklona koleba oko ovakvog poređaja. Broj poredanih molekula raste s brzinom vrtnje. Za iznos d-a, izražen indeksima loma tekućine u strujanju za dva međusobno okomita pravca, ova teorija daje izraz:
np - ns = Mη ν/r (4)
gdje je η koeficient viskoznosti, ν/r je radialni pad brzine na promatranom mjestu, dok je M t. zv. Maxwellova konstanta tekućine, reda veličine 10-10.
6. Električki dvolom (elektrooptički Kerrov efekt) sastoji se u tome, da homogeno izotropno tielo, dovedeno u jako električko polje, postane dvolomno, jer se svjetlost, koja titra uzporedno sa silnicama električkog polja, prostire kroz tielo drugom brzinom nego svjetlost, koja titra okomito na silnice. Takvo se tielo onda vlada kao ploča jednoosnog kristala izrezana paralelno s optičkom osi; ova je paralelna sa smjerom polja.
Pojav je odkrio J. Kerr (1875) na staklenoj prizmi, u koju su bile utaknute dvie elektrode spojene s polovima jednog induktora. Sumnje, da bi se moglo raditi o d-u, izazvanu mehaničkom deformacijom stakla pod djelovanjem električkog polja, uklonjene su, kad je Kerr g. 1879 odkrio isto djelovanje električkog polja u nevodljivim tekućinama. Napokon je Leiser (1911) dokazao električki d. i u plinovima.
 Sl. 14.
Sl. 14.Eksperimentalni je uređaj prikazan shematski u sl. 14. N1 i N2 su polarizator i analizator u ukrštenom položaju, CC je posudica s tekućinom (Kerrova stanica), P1, P2 su elektrode uronjene u tekućini u međusobnom razmaku h. Ravnine glavnog presjeka u N1 i N2, nagnute su prema smjeru električkog polja za ±45°. Kad se uzbudi električko polje, vidno se polje kod U razsvietli i ne da se posve zamračiti ni u jednom položaju analizatora. To pokazuje, da je svjetlost, koja je izašla iz tekućine, eliptički polarizovana. Pošto je titrajna amplituda komponente, koja titra u ravnini električkog polja, jednaka amplitudi komponente, koja titra okomito na tu ravninu, eliptičnost, a s njom i jakost svjetlosti, propuštene kroz analizator, zavise samo o razlici hoda među komponentama. Za razliku hoda Δ, izraženu u λ, našao je Kerr zakon:
Δ = B • 1 • E2, (5)
gdje l znači dužinu puta među elektrodama, u kome je električko polje homogeno, E = V/h je jakost polja (V = napetost među elektrodama), a veličina B je konstanta značajna za tekućinu ili uobće tvar među elektrodama. Dakle jakost razsvjete u točki U zavisi o jakosti polja nezavisno o njegovu predznaku. Izrazi li se 1 u cm, a E u elektrostatskim cgs jedinicama, B se zove Kerrovom ili elektrooptičkom konstantom. Ona je za tekućine većinom pozitivna (t. j. tekućina se vlada kao pozitivni jednoosni kristal), a reda je veličine 10-7. U nitrobenzolu i u nitrotoluolu B ima abnormno velike vriednosti: 346∙10-7 (nitrobenzol) i 121∙10-7 (nitrotoluol); obje su vriednosti za zelenu svjetlost. U plinovima B je reda veličine 10-10.
 Sl. 15.
Sl. 15.Vremenski razmak od uzpostavljanja električkog polja o porasta električkog d-a u tekućinama na podpuni iznos raci je od 10-8 sec., a vrieme od prekida električkog polja do nestanka električkog d-a reda je veličine 10-9 sec. Prema tome, ako se na P1 i P2 stavi visoka izmjenična napetost visoke frekvencije, električki d. sliedi titraje napetosti bez tromosti i onda, ako frekvencija nadilazi 106 hca, pa se električke oscilacije pretvaraju u oscilacije intenziteta svjetlosti, jer je jakost svjetlosti iz analizatora j = j0∙sin2δ/2, gdje je j0 jakost svjetlosti iz polarizatora, a δ je fazna razlika, koja odgovara razlici hoda. Na tome se osnivaju tehničke primjene električkog d-a (snimanje zvučnog filma; primanje kod bezžičnog prienosa slika) i neke njegove znanstvene primjene (mjerenje brzine svjetlosti: Gaviola 1926, Karolus i Mittelstaedt 1928). U sl. 15 prikazana je tehnička izvedba Kerrove stanice. Kao tekućina upotrebljava se nitrobenzol.
Električki d. tumači se tim, da molekuli tekućine, koji su po sebi električki i optički anizotropni, nastoje da se usuprot nesređenog termičkog gibanja orientiraju u smjeru električkog polja (Larmor 1898; Langevin 1910). Tako je pojav shvaćao već Kerr. U rezultatima teorija, razvijenih na ovoj osnovnoj misli, ima nekih razlika prema tome, da li se uzme, da molekuli nemaju permanentnog električkog momenta, nego da se ovakav stvori pod djelovanjem električkog polja, ili se molekuli predpostavljaju kao gotovi električki dipoli. Te se razlike odnose na predznak Kerrove konstante i na njezinu zavisnost o temperaturi.
I koloidne raztopine pokazuju d. u električkom polju. Ovaj je posljedica djelomične orientacije suspendiranih čestica u smjeru polja, a tim se izaziva optička anizotropija cielog disperznog sustava. D. raste s veličinom čestica, ali ne raste s kvadratom jakosti polja, nego u mnogo slučajeva krivulja porasta pokazuje zasićenost.
7. Magnetički dvolom. Kod njega razlikujemo tri vrsti pojava. a) Cotton-Moutonov efekt. Cotton i Mouton (1907) našli su, da nitrobenzol i α-bromnaftalin postaju dvolomni u vrlo jakom magnetskom polju, koje je upereno okomito na smjer prostiranja svjetlosti. Pojav su kasnije dokazali i iztražili na nizu čistih organskih tekućina. Pojav je magnetički analogon Kerrovu efektu, pa i eksperimentalni uređaj načelno odgovara onome u sl. 14, ako ondje zamislimo P1 i P2 kao čeone plohe vrlo jakog elektromagneta. Kod Cottona i Moutona tekućina se nalazila u cievi, koja je sprieda i otraga bila zatvorena staklenim pločicama bez unutrašnjih napetosti. Kad se uzbudi elektromagnet, vidno se polje iza analizatora slabo rasvietli (eliptička polarizacija). Tekućine moraju biti oslobođene od prašine, da bi se uklonio Majoranin efekt. Učinak je vrlo slab, pa se moraju upotrebljavati najosjetljivije metode za iztraživanje slabih d-a. Cotton i Mouton su iz svojih mjerenja našli za razliku hoda Δ među komponentom, koja titra paralelno s magnetnim poljem, i onom, koja titra okomito na nj, izraz analogan izrazu (5):
Δ = C • 1- H2, (6)
gdje je H jakost magnetskog polja, a C je konstanta reda veličine 10-12 (Cotton-Moutonova konstanta). Ona je najveća za nitrobenzol i za monobromnaftalin (2,9 i 2,7 • 10-12 za žutu svjetlost, kod 25°C). Njezina vriednost jako zavisi o temperaturi i o λ. Tekućina se u magnetskom polju vlada kao jednoosni kristal, većinom pozitivan, izrezan paralelno s optičkom osi; ova leži u smjeru polja. Pojav je zbog velikih eksperimentalnih potežkoća dosada malo iztraživan. Tumači se orientacijom molekula tekućine u smjeru magnetskog polja. U vrlo stlačenim plinovima (kisik i dušik kod 100 at) jedva je zamjetljiv.
b) Majoranin efekt. To je magnetički d. koji pokazuju koloidne raztopine u jakim transverzalnim magnetskim poljima. Odkrio ga je Qu. Majorana (1902). D. je vrlo često spojen s dihroizmom (v.), koji se sastoji u tom, da se nejednako absorbiraju komponenta, koja titra paralelno s magnetskim poljem, i ona, koja titra okomito na nj. Pokazuju ga i koloidne raztopine paramagnetičkih tvari i koloidne raztopine nekih diamagnetičkih tvari. I taj se pojav tumači orientacijom anizotropnih čestica suspenzije u magnetnom polju.
c) Voigtov efekt. Inverzni Zeemanov efekt (v.) popraćen je u blizini absorpcionih crta od magnetičkog d-a. Ovaj stoji u različitom utjecaju magnetskog polja na brzine prostiranja komponenata, koje titraju okomito na magnetsko polje i paralelno s njim. D. naglo raste s primicanjem absorpcionoj crti i ima na protivnim stranama suprotne predznake. Da se opažati samo najosjetljivijim metodama. Voigt ga je teoretski predvidio, a dokazali su ga gotovo istodobno sam on u zajednici sa Wiechertom i A. Cotton (1898).
LIT.: Erasmus Bartholinus, Experimenta crystalli islandici disdiaclastici, Hafniae 1669 (prievod: Ostwald’s Klassiker, br. 205); Ch. Huygens, Traité de la lumière, Leyde 1690 (prievod: Ostwald’s Klassiker, br. 20.); A. Fresnel, Oeuvres complètes, gv. II.-III., Pariz 1866—69; W. R. Hamilton, Rep. Brit. Assoc. 1833, 368; H. Lloyd, Phil. Mag. (3) 2, 112, 207, 1833; O. Lehmann, Wied. Ann. 40, 401, 1890; Ann. d. Phys. (4) 17, 728, 1905; 18, 796, 1905; D. Brewster, Phil. Trans. 1815, 60; 1816, 40. 156; F. Neumann, Pogg. Ann. 54, 449, 455, 1841; A. Seebeck, Schweiggers Journ. 7, 252, 382, 1913; 11, 471, 1814; 12, 1, 1814; A. Mesnager, Ann. Ponts Chauss., 4, 128, 1901; R. Lucas, C. R. 206, 827. 1938; Journal de physique (7) 10, 151, 1939; S. Oka, Kolloid-Ztschr. 87, 37, 1939; Ztschr. f. Phys. 116, 632, 1940; O. Wiener, Phys. Ztschr. 5, 332, 1904; J. C. Maxwell, Proc. Roy. Soc. 22, 46, 1873; Pogg. Ann. 151, 1874; A. Kundt, Wied. Ann. 13, 110, 1881; C. V. Raman a. K. S. Krishnan, Phil. Mag. (7) 5, 769, 1928; J. Kerr, Phil. Mag. (4) 50, 337, 1875; (5) 8, 85, 225, 1879; 13, 153, 248, 1882; P. Langevin, C. R. 151, 475, 1910; A. Cotton & H. Mouton, C. R. 145, 229, 1907; Ann. de phys. (8) 19, 153, 1910; 20, 194, 1910; Qu. Majorana, Lincei Rendic. (5) 11, 1, 374, 1902; W. Voigt, Gött. Nachr. 1898, 355; Wied. Ann. 67, 359, 1899; A. Cotton, C. R. 127, 953, 1256, 1898; 128, 294, 1899.
PREGLEDNA DJELA: F. Pockels, Lehrbuch d. Kristalloptik, Leipzig 1906; G. Szivessy, Kristalloptik, Besondere Fälle der Doppelbrechung (Geiger-Scheel, Handb. d. Physik, sv. XX., str. 635—904; sv. XXI., str. 724—884, Berlin 1929); E. G. Coker a. L. N. G. Filon, Photo-elasticity, Cambridge 1931; G. Mesmer, Spannungsoptik, Berlin 1939.M. K.