DIFRAKCIJA ili ogib (franc. i engl. diffraction) je zajednički izraz za velik broj fizikalnih pojava, koje nastaju, ako se širenje valova ograniči izvjesnim zaprekama. Dolaze li na pr. valovi, pobuđeni na površini vode, do dovoljno široke zapreke, nalazi se prostor iza nje u »sjeni«, koja je prilično dobro omeđena krajnjim zrakama, što izlaze iz ishodišta valova (sl. 1). Umanjujemo li zapreku, ulazit će valovi sve više u prostor geometrijske sjene, a kod dovoljno malene zapreke raširit će se po cijelom tom prostoru (sl. 2). Ovakav pojav, nazvan ogibom ili difrakcijom, javlja se jasno, ako je širina zapreke veličina istog reda s dužinom vala. Pojavi difrakcije postoje kod valova zvuka, svjetlosti, električnih valova, röntgenskih zraka, a i kod valova, koje pripisujemo najsitnijim materijalnom česticama.
Budući da su zvučni valovi dugi, na pr. 1 m, ogib je zvuka običan pojav, a sjene se zvuka slabo ističu. Baš obratno je kod svjetlosti, gdje nas sjene upućuju na pojam zrake i na t. zv. geometrijsku optiku, dok je ogib svjetlosti obično neprimjetljiv. U ostalom je pojam ogiba nastao baš u optici, gdje se taj pojav najlakše ispituje.
 Sl. 1. i Sl. 2. Širenje valova na površini vode sa zaprekama
Sl. 1. i Sl. 2. Širenje valova na površini vode sa zaprekama Sl. 2.
Sl. 2.Difrakcija svjetlosti. 1. Povijesni podatci. Često se opaža, da bačena sjena nije oštro ograničena. Na mjestima, koja bi se radi pravocrtnog širenja svjetlosti morala nalaziti u oštro ograničenoj sjeni, a djelomice i izvan tih mjesta, nalazi se nekoliko prelaznih svijetlih i tamnih pruga, ravnih ili zakrivljenih, koje se zovu pruge ogiba ili difrakcije.
Neke subjektivne pojave ogiba vidio je već Leonardo da Vinci. Motreći kroz rupicu u papiru zvijezdu opazio je, da je okružena s dva svijetla prstena. Objektivne pojave ogiba opisao je najprije F. Grimaldi sredinom 17. stoljeća. On se služio sunčanom svjetlosti i nazvao je te pojave difrakcijom (= »razbijanje«) svjetlosti. Grimaldijeve pokuse je nastavio Newton. On je radio i s homogenom svjetlosti. Našao je, da je razmak pruga to veći, što je slabiji lom svjetlosti. Sa stajališta svoje korpuskularne teorije svjetlosti tumačio je Newton ove pojave, koje je zvao infleksijom svjetlosti, pomoću privlačnih i odbojnih sila, kojima rubovi tijela, koje baca sjenu, djeluju na leteće čestice svjetlosti. Sa stajališta valne teorije pokušao je najprije protumačiti ogib Th. Young. On je uzeo, da pruge nastaju interferencijom zraka svjetlosti, koje prolaze blizu rubova tamnog tijela, i zraka, koje se na tim rubovima reflektiraju. Neosnovanost toga tumačenja pokazao je Fresnel time, da je isporedio ogibe na pukotinama sa svijetlim i pocrnjelim rubovima. Našao je, da je intenzitet pruga jednak u oba slučaja.
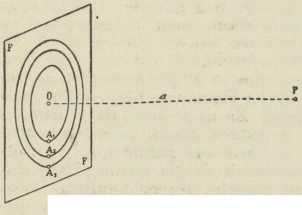 Sl. 3. Fresnelove zone
Sl. 3. Fresnelove zone2. Elementarna teorija ogiba. Fresnelove zone. Prema Huygens-Fresnelovu načelu iz fronte FF ravnog vala neka stižu prema točki P elementarni valovi s valnom dužinom λ (sl. 3). Titranje točke P je određeno superpozicijom sviju ovih elementarnih valova. Amplituda i faza ovog titranja može se odrediti računom. Iz točke P povući ćemo na ravninu FF okomice a — PO i oko »pola« O opisati takav red koncentričnih kružnica, da točka P bude od sviju točaka prve kružnice udaljena za a + λ/2, a od točaka druge kružnice za a + 2λ/2 i t. d. Lako se može izvesti, da su polumjeri nacrtanih krugova približno r1= √ aλ , r2= √ 2aλ .... a njihove površine παλ, 2παλ... Ravnina FF je tim razdijeljena u vijence, koji se zovu Fresnelove ili Huygensove zone. Kao prva ili centralna zona računa se najmanji krug. Radi jednake površine παλ sviju zona uzimamo, da iz svake od njih izlazi jednaka množina elementarnih valova.
Primjer: za zelenu svjetlost λ = 0,5 ∙ 10-3 mm kod a =1000 mm izlazi r1 = 0,7, r2, = 0,7 √ 2 mm.
Amplitude titraja u točki P, koje daju pojedine zone, označit ćemo redom sa z1, z2,... zn. Budući da razlici hoda λ/2 odgovara promjena faze 180º, skupno djelovanje sviju zona u točki P dobivamo tako, da s alternirajućim predznakom zbrojimo amplitude, koje daju pojedine zone. Imamo S = z1 — z2 + z3 — z4 + ... Veličine z1, z2,... zn zavise o daljini a te o kutu AnPO (sl. 3). Prijelazom na slijedeću zonu mijenja se zn neznatno. Približna elementarna teorija, kako ju je razvio engleski fizičar A. Schuster, daje rezultat:
S = z1/2 + zn/2 (n neparno); S = z1/2 — zn/2 (n parno).
Ako je valna ploha neograničena ravnina, djelovanje posljednje zone iščezava, te je S = z1/2, t. j. ravni val djeluje u točki P kao polovica centralne zone z1. Strožu teoriju različnih slučajeva ogiba razvili su Fresnel, zatim Kirchhoff, Sommerfeld, Schwarzschild, Rayleigh i dr.
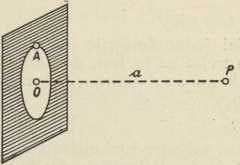 Sl. 4. Prolaz svjetlosti kroz
Sl. 4. Prolaz svjetlosti kroz
okrugao otvor3. Ogib na okruglom otvoru i okruglom zastorčiću. Na okrugli otvor s polumjerom OA = r u ravnini valne fronte neka dolazi val dužine λ (sl. 4). Uzet ćemo, da otvor obuhvaća malen broj n zona, i da svaka od njih jednako utječe na amplitudu titraja u aksijalnoj točki P. Iz formule S = z1/2 ± zn/2 slijedi, da je za taki broj n amplituda u točki P jednaka ništici, a za lihi S — z1.
U drugom je slučaju amplituda u točki P dvaput, a svjetleća četiri puta veća nego bez zaslona s otvorom. Maksimume i minimume svjetloće u aksijalnim točkama P dobivamo samo, ako otvor obuhvaća točno cijeli broj zona. Označimo li sa a okomicu PO, imamo √ a2 + r2 — a = nλ/2. Slijedi, da je približno a = r2/nλ. Ako je ovdje n neparan broj, izlazi u točki P maksimum, a ako je paran broj, minimum svjetloće. Odaberemo li točku P’ izvan osi PO, zamršeniji račun pokazuje, da ogibom nastaju svijetli i tamni kolobari, kojima je P središte. U sl. 5a, 5b vidimo fotografske snimke ogiba na otvorima, koji obuhvataju 2, odnosno 3 zone. Za n = 2 središte je tamno, a za n = 3 svijetlo, kako i teorija zahtijeva. Nalazi li se na mjestu O (sl. 4) mjesto pločice s rupicom okrugli zastorčić, možemo s pomoću Fresnelovih zona odrediti svjetloću u aksijalnoj točki P. Iz prijašnjih razmatranja slijedi, da na amplitudu u točki P utječe samo polovica prve zone izvan zastorčića. Ako je zastorčić dovoljno malen, djelovala bi ova zona jednako kao centralna zona, koju sad zastorčić pokriva. Slijedi, da se u središtu sjene zastorčića mora nalaziti mrljica sa svjetloćom, kao da zastorčića nema. Do važnog ovog rezultata došao je Poisson god. 1823 diskusijom opće Fresnelove teorije. Smatrajući ovaj rezultat apsurdnim i protivnim iskustvu, držao je Poisson, da Fresnelova teorija ne vrijedi. Međutim je Arago-ov pokus s okruglom pločicom posve potvrdio tu teoriju. Deslisle je već 1715 opazio svijetlu mrljicu u središtu sjene okrugle pločice, no na taj su pokus zaboravili. Slike 5c i 5d pokazuju snimke pokusa, kod kojih je zastorčić obuhvatio 2, odnosno 3 zone. U središtima obiju slika vidi se svijetla Poissonova mrlja.
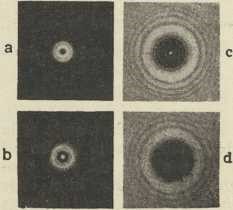 Sl. 5. Ogib svjetlosti na okruglom otvoru (a, b)
Sl. 5. Ogib svjetlosti na okruglom otvoru (a, b)
i na okrugloj pločici (c, d):
(po Arkadijevu) Sl. 6. Crtnja pločice po zonama
Sl. 6. Crtnja pločice po zonama
(po Woodu).4. Pločica sa zonama je staklena pločica, na kojoj je točno nacrtan velik broj Fresnelovih zona, kod čega je svaka druga zona načinjena neprozirnom. Na pr. može biti centralna zona prozirna, druga zona neprozirna, treća prozirna i t. d. Dolaze li na tu pločicu od udaljenog predmeta okomito svijetle zrake, stvarat će ona u određenoj »žarišnoj daljini« a optičku sliku poput zbirne leće. Takve slike nastaju i u daljinama 2a, ... a/2, a/4 ... Radi neprozirnih dijelova pločice otpadaju djelovanja zona s parnim rednim brojem (z2 = z4 =...= ø), a učinci zona s neparnim rednim brojem se zbrajaju. Na dvjema prozirnim zonama možemo uvijek odabrati po dvije korespondentne zrake, za koje je razlika hoda jednaka parnom broju λ/2. Na sl. 6 reproducirana je crtnja Fresnelovih zona, kakvu je načinio američki fizičar R. W. Wood (1898). Polumjeri nacrtanih krugova odnose se kao korijeni iz rednih brojeva 1, 2.. Fotografiranjem ovakvih crtnja dobivaju se negativi, koji ispunjavaju uvjete za pločice sa zonama (t. zv. Woodove pločice). Može se načiniti i dalekozor, kojemu je objektiv Woodova pločica s velikom žarišnom daljinom (na pr. a=50 cm), a okular pločica s malenom žarišnom daljinom.
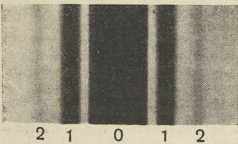 Sl. 8. Ogib svjetlost i na pukotini;
Sl. 8. Ogib svjetlost i na pukotini;
fot. negativ;
crvena svjetlost (po R. W. pohlu)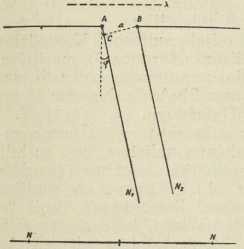 Sl. 7. Shema za ogib
Sl. 7. Shema za ogib
svjetlosti na pukotini5. Ogib na ravnoj pukotini. Na pukotinu AB, koja je usporedna s valnom frontom, neka dolazi ravni val dužine λ (sl. 7). Razmještaj svjetloće slike ogiba na vrlo udaljenom zastoru NN može se odrediti računom. Usporedni svežanj zraka AN1, BN2, koji sa simetralom pukotine zatvara kut φ, utječe na amplitudu titraja u točki N zastora iznosom, koji zavisi o razlici hoda δ krajnjih zraka AN1, BN2.
Načinimo li BC AN1,imamo δ = a sin φ, gdje je a širina pukotine. Elementarna teorija vodi do rezultata: mjesta minimalne svjetloće u tamnim prugama ogiba nastaju, ako je a sin φ=λ, 2λ, 3λ... Mjesta maksimalne svjetloće u svijetlim prugama ispunjavaju uvjete a sin φ = 0; 1,43λ; 2,459λ...
Slika 8 pokazuje pojav ogiba na 0,3 mm širokoj pukotini u daljini 1 m. Kraj široke srednje pruge, kojoj pripada glavni maksimum svjetloće, vide se 2 para sporednih pruga. Njihove svjetloće umanjuju se prema redu 1 : 1/20 :1/56.
Jednostavna teorija ogiba vrijedi, ako se daljina zastora od pukotine može smatrati beskonačnom. Fraunhofer je pokazao, da se mjesto udaljenog zastora može u koju god daljinu staviti zbirna leća i u njezinoj žarišnoj ravnini motriti slika ogiba. Pojav ogiba uz pomoć leće ili dalekozora nazvan je Fraunhoferovim ogibom. Radimo li bez leće, imamo Fresnelov ogib.
6. Optička mrežica (njem. Beugungsgitter, franc. réseau, engl. grating) jest pločica od kovine ili od prozirne tvari sa mnogo bliskih usporednih crta u jednakim međusobnim razmacima. Dolaze li valovi svjetlosti na takvu pločicu, mijenja se periodski od mjesta do mjesta intenzitet ili faza valova, koje ona reflektira ili propušta. Interferencijom ovih valova nastaju pojavi, nazvani spektri ogiba ili difrakcije.
Jednostavne optičke mrežice načinio je već Fraunhofer od usporednih tankih žica. Mnogo bolje mrežice izrađuju se tako, da se dijamantom, koji je montiran na stroju za dijeljenje dužina, režu blize crte na pločici. Ako je ta pločica prozirna, imamo transmisijsku ili propusnu mrežicu. Na kovnom zrcalu urezane crte daju refleksnu mrežicu. Krajem prošlog stoljeća dotjerao je H. A. Rowland (Baltimore, USA) tehniku izrađivanja ovakvih mrežica do velikog savršenstva. Načinjena je Rowlandova mrežica sa 110.000 crta na prostoru od 14,5 cm. Najveću optičku mrežicu, dugu 20 cm, visoku 10 cm, sa 500 crta na mm, načinio je američki fizičar A. A. Michelson. Ukupni broj crta na njoj iznosi 110.000, tako da bi sve crte, nanizane u jedan niz, dale dužinu 10 km.
Izrađivanje optičke mrežice težak je posao. I kraj automatskog rada najtočnijeg stroja za dijeljenje i opreznog postupka lako nastaju pogrješke. Dobre mrežice, kakve trebaju za spektralne aparate, vrlo su skupe i ima ih malo. Kopija kovne mrežice pravi se tako, da se strana s urezanim crtama polije rastopljenim celuloidom ili kolodijem. Kad se tekućina ispari, skine se oprezno kožica i fiksira na staklenoj pločici. Rezanje crta na staklu teže je nego na kovini. U spektralnim aparatima za vidljivu svjetlost dolaze većim dijelom refleksne mrežice, s 500 do 600 crta na mm.
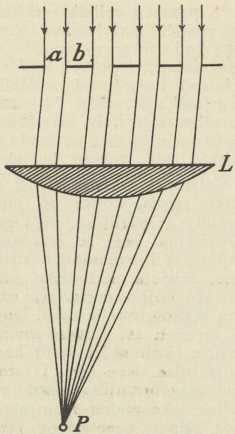 Sl. 9. Shema za ogib svjetlosti
Sl. 9. Shema za ogib svjetlosti
na nekoliko pukotinaTeorija mrežice. U elementarnoj teoriji smatra se propusna mrežica ravnim nizom usporednih pukotina. Uzmimo, da od vrlo udaljenog linearnog izvora dolazi svjetlost dužine vala λ okomito na takav niz pukotina (sl. 9). Usporedne zrake, koje iz pukotina izlaze, sabrane lećom L na način Fraunhoferov, neka interferiraju u točki P. Označimo sa φ kut ovih zraka s normalom na mrežicu, sa a širinu pukotine, sa b širinu zapreke, koja pukotine dijeli. Razlika hoda δ za svaki par zraka, koje izlaze iz susjednih pukotina, iznosi (a + b) sin φ. Zbroj a + b = d zove se konstanta mrežice. Njezinu vrijednost dobivamo, ako dužinu mrežice podijelimo s ukupnim brojem crta. Na mjestu P dobivamo maksimum svjetloće, ako je δ cijeli mnogokratnik od λ. Dolazimo tako do formule mλ=a sin φ (m = 0, 1, 2...), koja vrijedi za propusnu i refleksnu mrežicu. Radimo li s crvenom svjetlosti, pojav ogiba, koji nastaje u žarišnoj ravnini leće L, pokazuje niz I u sl. 10. Oko srednje pruge O, koja se nalazi u osi leće L i koja je izravna slika izvora svjetlosti, imamo s lijeva i s desna nekoliko pruga, koje odgovaraju rednim brojevima m = l, 2... Te su pruge to svjetlije i oštrije, što je veći ukupni broj crta mrežice i što je ona šira. Pruge 1, 2... zovemo spektrima ogiba reda 1, 2.... Niz II u sl. 10 pokazuje ogib za ljubičastu svjetlost. Veći razmak pruga reda I nego pruga reda II kazuje, da je veća dužina vala za crvenu svjetlost nego ljubičastu. Dolazi li na mrežicu bijela svjetlost, cijeli je spektar 1. reda odijeljen od spektra 2. reda. Spektri viših redova djelomično se prekrivaju, a njihove boje miješaju, što je naznačeno u slici 10-III. Da je red spektara ograničen, pokazuje slijedeći primjer: na mrežicu s konstantom d = 1/500 mm neka dolazi zelena svjetlost λ=0,0005 mm. Vrijednosti za m, sin φ = mλ/d, φ sabrane su u tablici
| m |
0 |
1 |
2 |
3 |
4 |
| sin φ = 0,25 m |
0 |
0,25 |
0,50 |
0,75 |
1 |
| φ |
0º |
14º |
30º |
49º |
90º |
Ovakva mrežica daje samo spektre 1., 2. i 3. reda. Mrežica s 1200 crta na mm daje samo spektar 1. reda.
Spektar mrežice ispunjava približno uvjet za normalni spektar, kod kojeg je promjena valne dužine svjetlosti razmjerna pomaknuću spektralne crte. Konkavna refleksna mrežica ispunjava točno taj uvjet. Svjetloća ovih spektara raste proporcionalno s kvadratom ukupnog broja crta mrežice. Radimo li s mrežicom od 10.000 crta, svjetloća je 108 puta veća, nego što bi je dala jedna pukotina omeđena s dvije crte.
 Sl. 10. Spektri mrežice za crvenu (I), ljubičastu (II) i bijelu (III) svjetlost
Sl. 10. Spektri mrežice za crvenu (I), ljubičastu (II) i bijelu (III) svjetlostS pomoću mrežice postizava se veća disperzija spektra nego s pomoću prizme. U formuli za mrežicu promjeni dužine vala dλ neka odgovora promjena kuta dφ. Za kutnu disperziju izlazi dφ = m/d cosφ dλ. Uzet ćemo, da na mrežicu sa 500 crta na mm dolazi natrijeva svjetlost, sastavljena od valnih dužina λ = 0,5890 μ, λ + dλ = 0,5896 μ. Za kutnu disperziju spektra 1., 2., 3., reda izlaze redom vrijednosti 1,1'; 2,5'; 6,5'.
Za snagu razlučivanja (pouvoir de résolution, resolving power, Auflösungsvermögen) u spektru ogiba vrijedi Rayleighova formula R = λ/dλ = Nm, u kojoj je m red spektra, a N ukupni broj crta mrežice. S pomoću velikih mrežica može se za vidljivu svjetlost postići maksimalno R = 300.000, koje je mnogo veće nego kod spektra prizme.
U spektru mrežice javljaju se zanimljivi pojavi, koji se zovu lažne crte ili dusi (engl. ghosts). Potječu od različnih pogrješaka mrežice. Nijedna mrežica nije tako savršena, da bi razmaci crta na svakom mjestu bili točno jednaki.
Valjanost mrežice zavisi o vijku stroja, kojim se ona izrađuje. Opazili su, da i na mrežicama, koje su izrađene najboljim Rowlandovim strojem, postoje periodičke pogrješke, koje se ponavljaju nakon svakog okreta vijka. One su izvor t. zv. Rowlandovim dusima, koji se javljaju kao dvije blize slabe crte. U sredini između njih nalazi se uvijek jaka realna spektralna crta. Radi simetričnog razmještaja Rowlandove se lažne crte Iako raspoznaju i ne zamjenjuju se s realnim crtama. Njihova je svjetloća proporcionalna s kvadratom reda spektra.
Optičke mrežice mogu imati i drukčije periodičke, a i neperiodičke pogrješke. U nekim slučajevima javljaju se lažne crte s obiju strana realne crte, no dosta daleko od nje. Ovakve pojave istraživali su M. Lyman i R. W. Wood. Oni su našli metode, s pomoću kojih se može prosuditi, je li neka crta realna ili lažna.
Optička mrežica, ugrađena mjesto prizme u spektralni aparat, omogućuje jednostavno i točno mjerenje dužine vala svjetlosti. U tom je važna njezina upotreba. Za mjerenje dužine vala ultracrvenih zraka služe mrežice s malenim brojem crta na mm i mrežice od tankih žica.
 Sl. 12. Ogib homogene svjetlosti
Sl. 12. Ogib homogene svjetlosti
na ultra zvučnim valovima u tekućini;
negativ; (D. P-ć 1935)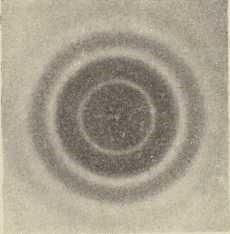 Sl. 11. Ogib homogene svjetlosti
Sl. 11. Ogib homogene svjetlosti
na sitnim česticama: Fot. negativ
(po R. W. Pohlu)7. Ogib na sitnim česticama. Atmosferski pojavi ogiba svjetlosti. Ako kroz staklo, na kojem se nalazi mnogo zrnaca prašine ili vodenih kapljica, nastalih kondenzacijom, motrimo daleki izvor svjetlosti, vidjet ćemo, da je okružen vijencem. Da se ovaj pojav osniva na ogibu svjetlosti, pokazao je već Fraunhofer. Gledamo li homogeni izvor svjetlosti, izmjenjuju se svijetli i tamni kolobari vijenca, kako pokazuje sl. 11. Kolobari su to veći, što su sitnija zrnca ili kapljice. S pomoću formule sin φ= 3/2 λ/a, koja vrijedi i za ogib svjetlosti na sitnoj čestici, možemo izračunati promjer čestice a. Vidimo li na pr. kod crvene svjetlosti λ = 0,7 μ polumjer prvog svijetlog kolobara pod kutom φ = 2º, izlazi a = 30 μ. Vijenac oko bijelog izvora svjetlosti ima boje Newtonovih koluta.
Sitne čestice vode ili leda u zraku mogu izvesti pojav ogiba. Neposredno oko Mjeseca opažamo često jedan ili više svijetlih vijenaca (engl. halo, njem. Hof). Nutrašnja strana vijenca redovno je bijela, a prema vanjskoj strani slijede prelazne boje: modra, crvena, žuta. Boje su to jasnije, što su čestice jednoličnije. Prema teoriji, koja vrijedi za ogib svjetlosti na sitnim kuglastim česticama, promjeri svijetlih kolobara homogene svjetlosti odnose se kao 1 : 1,83 : 2,76. Za ogib svjetlosti na iglicama leda, koje imaju presjek pravokutnika, vrijede omjeri 1 : 2 : 3. Mjerenjem se može prosuditi, imamo li ogib na vodenim kapljicama ili na ledenim iglicama. Veliki bojadisani kolobari oko Mjeseca s polumjerima 22º i 46º jesu pojav disperzije svjetlosti na ledenim iglicama.
8. Ogib svjetlosti na ultrazvučnim valovima. S pomoću pločica od kvarca i turmalina, koje u visokofrekventnom električnom polju titraju radi piezoelektričnog djelovanja, stvaraju se u tekućinama i plinovima valovi visoke frekvencije, nazvani ultrazvučnim valovima (→ akustika 3). Ako je njihova dužina vala dosta malena, čine oni t. zv. ultrazvučnu mrežicu, koja se prema svjetlosti vlada slično kao obična optička mrežica. Konstanta je ultrazvučne mrežice kod stojnih i progresivnih valova ista i jednaka cijeloj dužini vala. Na ultrazvučnu mrežicu može se primijeniti formula, koja vrijedi za optičku mrežicu. Ogib svjetlosti na ultrazvučnim valovima otkrili su 1932 Debye i Sears te Lucas i Biquard.
Na sl. 12 snimljen je ogib žute natrijeve svjetlosti na ultrazvučnoj mrežici u alkoholu. Vide se spektri 0., 1., 2. i 3. reda. Za pokus je služila kvarcova pločica 25X25X0,9 mm, koja je, uzbuđena na osnovnu frekvenciju 3,200.000 titraja u sek., titrala u tekućini smjerom svoje debljine. Dužina ultrazvučnog vala bila je Λ = 0,042 cm, tako da na 1 cm dolazi 23,8 Λ. Otkriće Debyea i Searsa daje jednostavnu metodu za mjerenje brzine zvuka u tekućinama. Kod ove metode treba vrlo malena količina tekućine.
Za druge pojave ogiba → röntgenske zrake, → elektron.
LIT.: R. W. Wood, Physical Optics, III. izd., New York 1934; R. W. Pohl, Einführung in die Optik, 4. i 5. izd., 1943.D. P-ć.