DALEKOZOR. Ako udaljen predmet ne vidimo dosta jasno, nastojimo da mu se približimo. Približavanjem postaje veći vidni kut, t. j. kut, što ga čine pravci povučeni od oka prema dvjema točkama predmeta, a povećava se i množina svjetlosti, koja od predmeta ulazi u oko. Ako se ne ćemo ili ne možemo približiti, postizavamo povećavanje vidnog kuta i veće obilje svjetlosti na taj način, da predmet motrimo kroz dalekozor, dogled, staklo, durbin, teleskop. (Perzijski: dur »daleko«, bin »vid«; grč. τήλε »daleko«, σϰοπέω »motrim«).
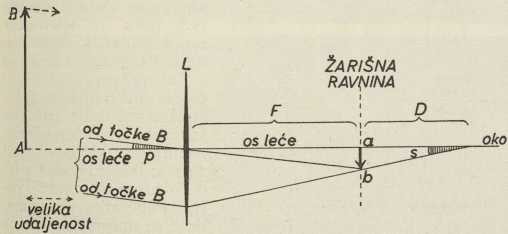 Sl. 1. Povećanje jednom lećom
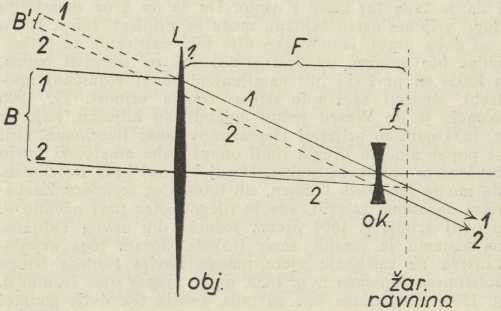
Sl. 1. Povećanje jednom lećomJedna leća kao dalekozor. Najjednostavniji dalekozor bila bi jedna jedina zbirna leća. Ako je os leće L (sl. 1) upravljena prema točki A vrlo udaljenog predmeta AB, zrake svjetlosti, što padaju od predmeta na leću, lećom se lome i stvaraju sliku ab u žarišnoj ravnini leće, te je u toj ravnini žarište leće a slika točke A; udaljenost F od leće do žarišta zove se žarišna daljina. Slika točke B nalazi se tamo, gdje pravac, povučen od B kroz sredinu b leće, zgađa žarišnu ravninu. U točki B sastaju se iza prolaza kroz leću sve zrake, što dolaze od B, kao što se u a sastaju zrake, koje su došle iz A. Slika ab je dakle s obzirom na predmet AB obrnuta. Ako je predmet dosta svijetao, možemo sliku njegovu uhvatiti na bijel zastor i motriti je. Nema li zastora, slika lebdi u zraku, pa i tu sliku možemo vidjeti, ako oko O smjestimo u os leće još dalje od žarišne ravnine. Kut s, pod kojim pri tome vidimo sliku, postaje veći, ako D, udaljenost oka od slike, smanjujemo. Ako je D < F, taj je kut veći od kuta p, pod kojim vidimo sam predmet, i leća postaje dalekozor. Omjer kutova s : p zove se povećanje. On je jednak F : D, te je za odabranu leću, t. j. kraj odabranog F, povećanje obrnuto razmjerno sa D. Međutim za približavanje postoji kod svakoga oka granica, te dobrovidno oko odrasla čovjeka ne može jasno vidjeti na udaljenosti manje od kojih 25 cm, tako da je za takvo oko najveće moguće povećanje F : 25 (F u cm). Ako je leća prejaka, te je F < 25 cm, povećanje je nemoguće.
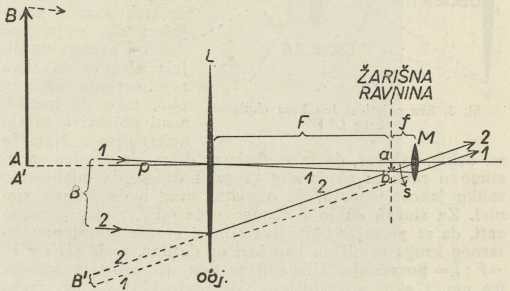 Sl. 2. Načelo Keplerova dalekozora
Sl. 2. Načelo Keplerova dalekozoraKeplerov dalekozor. Niti je povećanje, što se jednom lećom dobije, znatno, niti je vidno polje pri tom jednostavnom uređaju široko, tako da se jedna leća ne upotrebljava kao dalekozor. Dalekozor dobijemo, ako leći L dodamo drugu zbirnu leću M, i to leću malene žarišne daljine f (sl. 2). Kroz tu leću motrimo sliku ab od prilike onako, kako se lupom (jednostavnim sitnozorom) sitni predmeti vide povećani. Budući da lupa pokazuje predmet uspravno, a slika je ab obrnuta, takav će dalekozor pokazivati predmet obrnuto. Tako složen d. zove se Keplerov, jer ga je Kepler prvi opisao.
Leća L d-a, jer je okrenuta prema predmetu (objektu), zove se objektiv, leća M, jer je bliža oku, zove se okular. U astronomiji, gdje Keplerov d. ima golemu važnost, taj se d. često zove refraktor (»koji lomi«), za razliku od drugog astronomskog d-a, koji se zove reflektor (»koji odbija«), a objektiv mu nije leća i ne lomi svjetlosti, nego zrcalo, te odbija svjetlost.
Za dobrovidno oko stavlja se okular u takvu daljinu od slike ab, da je a, žarište objektiva, ujedno i žarište okulara. U tom slučaju zrake, koje su prošle kroz koju god točku b slike ab, poslije loma u okularu idu usporedno; na oko te zrake tako djeluju, kanda su došle iz beskrajno udaljene točke B', koja je prema tome slika točke b, t. j. slika slike točke B. Kod takvog namještaja slike dobrovidno oko gleda bez napora akomodacije.
Kao kod leće tako je i ovdje povećanje (kuta) s : p. Iz sl. 2. slijedi, da je približno s : p = F: f, t. j. povećanje se nađe tako, da se žarišna daljina objektiva podijeli sa žarišnom daljinom okulara. Prema tome, da povećanje bude veliko, treba da objektiv ima veliku žarišnu daljinu, a okular malenu; drugim riječima, objektiv je »slaba« leća, okular »jaka«. Ako na pr. objektivu, kojemu je F = 17 m (na Lick-zvjezdarnici), dodamo okular za f = 10 cm = 0∙1 m, povećanje je 170-struko. (Neka je spomenuto, da leća ima dva žarišta, od kojih se kod tanke leće jedno nalazi toliko daleko ispred leće, koliko je drugo daleko iza leće; kod Keplerova d-a zanimaju nas stražnje žarište objektiva i prednje žarište okulara).
Prirodno je, da se objektiv i okular sjedinjuju na taj način, da se d-u dade oblik cijevi, koja je na jednom kraju zatvorena objektivom, na drugom okularom. Duljina je te cijevi određena zbrojem žarišnih daljina objektiva i okulara F + f. Objektiv i okular treba da su dobro centrirani, t. j. površine (kuglaste) leća treba da imadu svoja središta u jednom istom pravcu, koji se zove os d-a. Od objektiva tražimo, da ima dosta velik promjer, tako da hvata mnogo svjetlosti, te je on daleko najskupocjeniji dio d-a. Okular se dade lako ukloniti i zamijeniti drugim, na pr. da se dobije drugo povećanje. Njegov se smještaj lako mijenja, te za kratkovidno oko, kojemu vid nije ispravljen naočarima, treba primjereno smanjiti udaljenost okulara od objektiva.
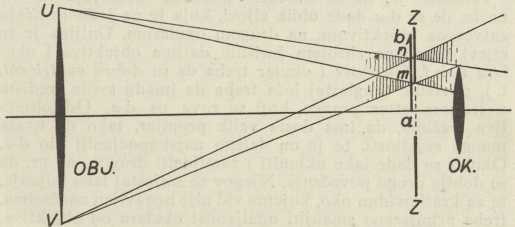 Sl. 3. Sva svjetlost ide kroz okularni krug U' V'
Sl. 3. Sva svjetlost ide kroz okularni krug U' V'Okularni krug. Ako Keplerov d. danju upravimo prema nebu, možemo iza okulara na bijel papir uhvatiti sliku U'V', koju okular načini od objektiva UV (sl. 3). U'V' je svijetao krug, jer rub objektiva ima oblik kružnice. Taj se krug zove okularni krug. Sva svjetlost, koja prođe kroz objektiv i okular bez odbijanja i stramputica, mora proći kroz okularni krug. Svagdje drugdje iza okulara zrake svjetlosti ispunjaju širi prostor nego li na mjestu okularnog kruga; tu se skup svih svežnjeva svjetlosti najviše suzuje.
Ako je promjer okularnog kruga manji od promjera očne zjenice i ako oko zgodno namjestimo, moći će sva svjetlost, koja je prošla kroz d., ući u oko. Naprotiv, ako je U'V' veće od promjera zjenice, ne možemo toga postići. Na zjenicu može onda pasti samo dio slike objektiva, iz čega onda slijedi, da u tom slučaju pri motrenju udaljenoga predmeta upotrebljavamo samo jedan dio objektiva, dok od preostalog dijela njegova nikakva svjetlost ne ulazi u oko, tako da mogućnosti objektiva ostaju neizrabljene. Nameće se, dakle, zahtjev, da tako gledamo d-om, da zjenicu smjestimo u ravninu okularnog kruga, i drugo, da odaberemo toliku jakost okulara, da okularni krug bude jednak zjenici. Za slučaj, da je F mnogo veće od f, može se pokazati, da se promjer objektiva odnosi prema promjeru okularnog kruga približno kao žarišne daljine, te je UV : U'V’ = F : f = povećanje. Uzme li se, da je promjer zjenice 0∙6 cm, i ako se zahtijeva, da bude U'V' = 0∙6, treba onda uzeti povećanje UV : 0∙6. Uz manje povećanje ne bi bila izrabljena cijela širina objektiva. Uostalom, promjer se zjenice mijenja, te se ona pri motrenju svjetlijih predmeta suzuje; ako taj promjer pri motrenju punoga mjeseca iznosi samo 0∙2 cm, treba u tom slučaju prijeći na veće povećanje UV : 0∙2.
Budući da se površine dvaju krugova odnose kao kvadrati njihovih promjera, izlazi uz takvo povećanje, da je omjer množine svjetlosti, koja ulazi u d., prema množini, koja bi ulazila u prosto oko, jednak kvadratu povećanja. Premda se od svjetlosti, koja pada na d., jedan dio gubi refleksijama i apsorpcijom u staklu, ipak nam spomenuti omjer pruža uporište za prosuđivanje, koliko puta više svjetlosti ulazi u oko, kada gleda kroz dalekozor, nego kad gleda bez njega.
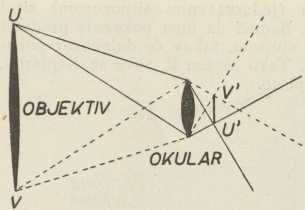 Sl. 4. Ograničenje vidnoga polja
Sl. 4. Ograničenje vidnoga poljaNeka ab (sl. 4) znači sliku udaljenog predmeta, koju je načinio objektiv. Nameće se pitanje, koliko od te slike vidimo kroz okular. U sl. 4 prikazan je svežanj zraka, koji je, prošavši kroz objektiv UV, stvorio točku n slike, a dotiče se okulara izvana. Točka n jest na granici vidljivosti. Točke, koje su bliže osi d-a nego li točka n, dakle komad an slike, vide se kroz okular, dok se točke udaljenije, naime komad nb slike, ne vide. U drugu ruku, svežanj zraka, koji je stvorio točku m slike, dotiče rub okulara iznutra, te je m krajnja točka među onima, od kojih sve zrake, koje su točku-sliku stvorile, pogađaju okular. Sve točke, koje bliže osi nego li točka m, vidimo kroz okular u punoj svjetlosti objektiva, dok dalje od m, prema n, svjetloća opada. Da ne smeta to padanje svjetloće, ono se naprosto tako ukloni, da se u ravninu slike ab stavi zaslon ZZ, i to crn okrugao prsten, kojemu je unutarnji polumjer am. Time se, doduše, vidno polje smanji, ali samo za jedan rub manje vrijednosti, jer je nejednake svjetloće.
Veličina vidnoga polja d-a određena je kutom v, što ga čini os d-a sa zrakama, koje dolaze u oko od ruba vidnoga polja. Predmet, kojemu slika u d-u seže od sredine do ruba vidnoga polja, bez dalekozora se vidi pod kutom, koji mjeri »pravo« vidno polje. Taj se kut približno izračunava tako, da v podijelimo s povećanjem.
Objektiv i okular D., kako je do sada opisan i kako se isprva gradio, ima veliku manu. Zrake, koje iz svijetle točke padnu na leću, lećom se lome, a iza toga trebalo bi da se sastanu u jednoj točki, slici svijetle točke. No objektiv, koji je jedna jedina leća, ne može tomu zahtjevu dobro udovoljiti. Jedno zato, što se zrake raznobojne svjetlosti, na pr. žute i modre, ne lome jednako, te se sastaju na različnim mjestima; a drugo zato, što se ni zrake svjetlosti iste boje, koje su izašle iz jedne točke i prošle na različnim mjestima kroz objektiv, ne će sastati baš u jednoj točki. Slično vrijedi o okularu, ako je on samo jedna leća. Poradi te kromatične i sferne aberacije (→ aberacija 2, → akromatičnost) slike, dobivene najstarijim d-ima, bile su loše, i nikako se nisu dala tim spravama postići znatnija povećanja.
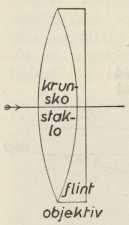
Trebalo je u prvom redu riješiti zadaću, da se aberacija ukloni za žarište objektiva, tako da se zrake zvijezde, na koju je uperena os d-a, sve sastanu u tom žarištu. Sferna aberacija sama dala bi se ukloniti, kako je Descartes pokazao, kada bismo za objektiv uzeli leću, kojoj nisu obje površine kuglaste. Međutim je Huygens našao, da se ta aberacija lakše uklanja, ako se za objektiv uzme sustav od dvije leće kuglastih površina, jedne jače, zbirne, i druge slabije, rastresne; te su leće sasvim blizu jedna drugoj, te skupa djeluju kao jedna zbirna leća, a ako se zgodno odaberu četiri polumjera krivosti površina jedne i druge leće sastavnice, može se sferna aberacija ukloniti. To ide, kako račun pokazuje, čak na bezbrojno mnogo načina. Da nestane i kromatična aberacija, uzme se jedna leća, zbirna, od krunskoga stakla, druga, rastresna, od flintova stakla, pa se i tu može zgodnim izborom polumjera krivosti postići željeni cilj (→ akromatičnost). Uvjeti, koji se jednim i drugim zahtjevom stavljaju izboru polumjera krivosti, ne protuslove jedni drugima nego se dopunjuju i još uvijek ostavljaju bezbroj mogućnosti za građenje akromatičnog objektiva. Redovno je krunsko staklo na prednjoj, izvanjoj strani objektiva, tako da svjetlost, udarajući u d., zgađa najprije krunsku leću objektiva (Sl. 5a).
 Sl. 5a.
Sl. 5a.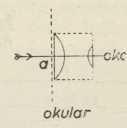 Sl. 5b.
Sl. 5b.Što se tiče uklanjanja aberacije kod okulara (v.), neka je spomenut samo okular, koji je izumio Ramsden, koji se u zvjezdarnicama najčešće upotrebljava, a sastoji se od dvije jednako jake plankonveksne leće, načinjene od iste vrsti stakla; leće su jedna prema drugoj okrenute svojim pupčastim stranama, dok su im ravne strane okrenute prema objektivu, dotično oku (sl. 5b). Obje leće razmaknute su jedna od druge za nešto manje nego što je njihova žarišna daljina, tako da se rezultujuće žarište a okulara nalazi nešto malo izvan okulara. Uz primjenu toga okulara polumjer vidnog polja može iznositi do 30°.
Utjecaj ogiba. Dovle se djelovanje dalekozora razmatralo s gledišta t. zv. geometrijske optike, nauke, koja se osniva na pojmu zrake svjetlosti i na zakonima odbijanja i loma. Međutim nauka o valovima svjetlosti u skladu s iskustvom pokazuje, da takvo razmatranje u skrajnjim zaključcima nije više valjano. Zrake, koje dolaze od udaljene svijetle točke, na pr. zvijezde stajačice, i prođu kroz objektiv, mogu se po računima geometrijske optike makar savršeno točno sastati u jednoj točki, pa ipak se u zbilji u toj točki ne sabere sva svjetlost, već poradi ogiba (→ difrakcija) nastaje oko te točke zamršenija podjela svjetlosti, koja se može vidjeti dovoljno jakim okularom. Umjesto točke vidi se svijetao krug, kojemu svjetlost pada prema rubu, i oko kruga koncentrični kolobari, bojadisani, ako je svjetlost sastavljena, kako to obično biva (sl. 6.)
 Sl. 6. OGIBNI KRUG (Negativ)
Sl. 6. OGIBNI KRUG (Negativ)
(Pohl, Optik)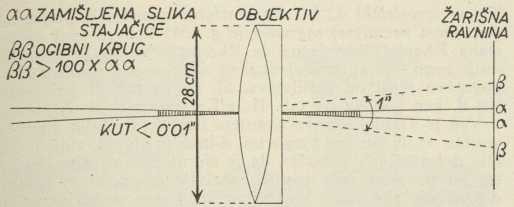 Sl. 7. UTJECAJ OGIBA
Sl. 7. UTJECAJ OGIBA
(Sitne veličine u crtnji su krupne i nerazmjerne).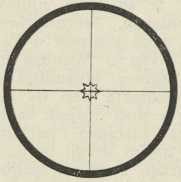 Sl. 8.
Sl. 8.
Zvijezda usred vidnog poljaS obzirom na to, da svjetlost kolobara daleko zaostaje za svjetloćom kruga, glavni je učinak ogiba taj ogibni krug. On eto nadomješta točku, koju bismo htjeli dobiti kao sliku točkastog izvora svjetlosti. (Kada objektiv ne bi bio omeđen krugom, već otvorom drugoga oblika, na pr. trokutom, izašao bi i pojav ogiba drukčiji).
Ako upravimo d. prema dvojnoj zvijezdi, t. j. k dvjema stajačicama, koje su na nebeskom svodu blizu jedna drugoj, te ih prosto oko vidi kao jednu zvijezdu, ne ćemo moći d-om jednu zvijezdu od druge razaznati ni odličnim objektivom ni uz najveće povećanje, ako su ogibni krugovi zvijezda preveliki, te se djelomice poklapaju. Uopće je za upoznavanje tančina u d-u važno, da ogibni krug bude što manji. Općenito se može reći, da je ogibni krug to manji, što je veći promjer D objektiva. Tako ako je D = 28 cm, ogibni je krug ββ (sl. 7) u žarišnoj ravnini objektiva tolik, da bismo ga obuhvatili iz sredine objektiva kutom 1″. No po onome, što se znade o veličini i udaljenosti stajaćica, izlazi, da su prividni promjeri i najvećih i najbližih stajaćica manji od 0∙01″. Prividnoj veličini 0∙01″ odgovarala bi prema geometrijskoj optici kod spomenutog objektiva slika αα, kojoj je promjer samo 0∙01 promjera ogibnoga kruga. Ta se pomišljena slika tako reći sva utapa u ogibnom krugu, tako da se oblik stajaćice današnjim d-ima ne može razabrati. Ni desetak puta širi objektiv ne bi za to imao dosta malen ogibni krug.
Dva objektiva jednakih promjera D, ali različitih žarišnih daljina F, načinit će ogibni krug to veći, što je veće F, te je polumjer ogibnog kruga F : D × 0 00067 mm. On je obrnuto razmjeran s veličinom D : F, koju zovemo omjer otvora objektiva. Da uzmognemo u d-u razaznati što više tančina motrenoga predmeta, treba dakle da bude omjer otvora primjereno velik.
Primjeri. Različiti su uzroci, koji ograničuju veličinu D : F. Prvo, veliki refraktori imadu veliku žarišnu daljinu F, da već slika, koju objektiv načini, bude velika; leće takvog objektiva imadu vrlo slabo zakrivljene površine; za njih se aberacije dadu lakše ukloniti nego li kod jače zakrivljenih površina. Što se pak tiče samoga D, on se ne može odabrati veći od nekoliko decimetara, jer je teško načiniti tako veliko staklo dovoljno jednolično (homogeno). Osim toga leća velikoga promjera mora biti radi čvrstoće svoje primjereno debela, a u staklu se svjetlost apsorbira. Pogotovu se jako apsorbiraju zrake ljubičaste i ultraljubičaste svjetlosti, koje dolaze u obzir, kada okular d-a nadomjestimo fotografskom komorom. Uzme li se dakle prevelik objektiv, gubitak je svjetlosti radi apsorpcije na putu kroz debelu ploču veći nego što se naknađuje obiljem svjetlosti, koja pada na široku površinu objektiva. Kraj danas poznatih vrsta stakla može se uzeti, da je kod dalekozora, koji ima služiti fotografiranju, granica za veličinu objektiva, ako je taj složen od dvije leće, D = 5 do 6 dm; kod još širih objektiva apsorpcija postaje prevelika. Za objektive d-a, koji služe vizualnom istraživanju, granica je nešto viša.
U tablici popisani su neki najznatniji objektivi refraktora, i to njihov otvor D, žarišna daljina F, omjer otvora, godina namještanja i zvjezdarnica.
| D (cm) |
F (m) |
D:E |
god. |
tvorničar |
zvjezdarnica |
| 24 |
4∙3 |
1:18 |
1824 |
Fraunhofer |
Dorpat |
| 69 |
10∙5 |
1:15 |
1878 |
Grubb |
Beč |
| 91 |
17∙6 |
1:19 |
1888 |
Clark |
Mt. Hamilton (Lick zvjezd.) |
| 102 |
19∙3 |
1:19 |
1897 |
Clark |
Williamsbay, Wisc. (Yerkes-zvjezd.) |
| 80fot. |
12∙0 |
1:15 |
1905 |
Steinheil, Repsold |
| 50 |
12∙5 |
1:25 |
|
Potsdam |
Malen Keplerov d. pokazuje sl. 4a na tab. II.; promjer objektiva iznosi mu 5∙3 cm. Najveći današnji refraktor, dar Yerkesov, s objektivom od 102 cm (40 palaca), prikazan je u sl. 2. na tab. I., dok je u sl. 1. na tab. II. Potsdamski instrumenat, u kojemu su sjedinjena dva refraktora, jedan za gledanje, drugi za fotografiranje, te su im objektivi sračunati s obzirom na zrake važne za oko, dotično za fotografsku ploču.
Važnost d-a za mjerenja. Keplerov d. za astronomiju nije samo po tom važan, što pokazuje nebeske pojave, kojih bez njega ne primjećujemo, nego i zato, što omogućuje veliku točnost astronomskih mjerenja. Da nam d. posluži pri mjerenju lukova na nebeskom svodu, treba mu dodati uređaj, kojim se može izmjeriti smještaj zvijezde u vidnom polju; u prvom redu uređaj, kojim se može zvijezda dovesti baš u sredinu vidnoga polja. U tom je slučaju os d-a upravljena prema zvijezdi, te kažemo, da zvijezdu viziramo. Središte se vidnog polja za tu svrhu na taj način obilježuje, da se u žarišnu ravninu objektiva stavi križ od niti (na pr. niti iz čahure običnoga pauka), i to tako, da je presjek niti baš u žarištu, dakle u osi d-a. Kada zvijezdu kroz okular vidimo oštro, vidimo oštro i nitni križ, jer je nitni križ na istom mjestu, gdje je i slika zvijezde, koju je načinio objektiv. Zvijezdu viziraramo, kada je vidimo baš u presjeku niti (sl. 8.).
Malen Keplerov d. nalazi se kao sastavni dio u mnogim fizikalnim i drugim spravama i uređajima, poimence mjeračima, tako kod goniometra, katetometra, spektroskopa, kod Poggendorffove metode za mjerenje zakreta zrcala u mjeračima spravama i t. d.
 Sl. 9. Načelo Galilejeva dalekozora
Sl. 9. Načelo Galilejeva dalekozoraGalilejev dalekozor. Stariji od Keplerova je Galilejev d., koji se zove također holandijski. Bitno se razlikuje od Keplerova time, što mu je okular rastresna leća. Taj se okular stavlja bliže objektivu nego što je samo žarište objektiva, tako da svjetlost, došavši iz objektiva, prije udara na okular, nego što bi načinila sliku predmeta. I ovdje kao kod Keplerova d-a za dobrovidno se oko, koje motri udaljen predmet, okular tako smješta, da se žarište okulara i žarište objektiva podudaraju. No dok se kod Keplerova d-a u tom slučaju stavlja u žarište objektiva prednje žarište okulara, kod Galilejeva dolazi na to mjesto stražnje žarište okulara. Da se razumije djelovanje toga okulara, treba imati na umu, da zrake, koje su ispred okulara upravljene prema jednoj točki stražnje žarišne ravnine okulara, prošavši kroz okular, postaju usporedne. Prema tomu zrake, koje su od udaljene svijetle točke B pale na objektiv i iz objektiva se navratile (konvergirale) prema jednoj točki žarišne ravnine objektiva, okularom se rasiplju, te postanu usporedne, kao da dolaze od beskrajno udaljene točke B', slike, koju je d. stvorio od točke B. U sl. 9 crtane su dvije zrake, koje dolaze od B; jedna, koja ide sredinom objektiva, te se lomi u okularu, i jedna, koja ide sredinom okulara, pošto se lomila u objektivu. Iz tog crteža izlazi, da oko vidi u tom d-u predmet uspravno. Povećanje Galilejeva d-a jest kao i kod Keplerova jednako omjeru žarišne daljine F objektiva i žarišne daljine f okulara, t. j. F : f.
Nedostatci toga d-a prema Keplerovu jesu manja veličina vidnoga polja, nejednaka svjetloća toga polja, a i to, da se u njemu ne daju smjestiti onakvi uređaji za mjerenja kao u Keplerovu. Prednost mu je, da predmet pokazuje uspravno, da se odlikuje znatnom svjetloćom i, najposlije, da mu je dužina dana veličinom F—f, te je on kraći nego li Keplerov d. jednakog objektiva i jednakog povećanja. Potonje svojstvo dolazi osobito u obzir kod neznatnih povećanja, na pr. dvostrukog, jer onda razlika između F i f nije velika, pa je zato znatna razlika između F — f i F + f. Prema tome Galilejev se d. gradi samo za malena povećanja; u milijunima primjeraka nalazi se on u porabi kao kazališni durbin, mornarski d. i t. d. i to kao dvostruk d. (za dva oka određeni, binokularni).
Povijesni podatci. Kako je i kada nastao prvi d., ostat će možda zauvijek neriješeno pitanje. D-i Galilejeve vrsti javljaju se u Holandiji oko g. 1608, te se izum njihov često pripisuje Lipperheyu, a i Janssenu, tvorničarima naočara u Middelburgu. Sam Galilei, tada profesor u Padovi, doznao je za jednog svog boravka u Mlecima g. 1609, da se u Parizu mogu dobiti sprave holandijskog porijetla, koje pokazuju udaljene predmete kao da su blizu. Vrativši se u Padovu već se prve noći dosjeti, kako treba takvu spravu graditi, te je odmah sutradan i načinio svoj prvi d.; nekoliko dana kasnije načini drugi, bolji, i odnese ga duždu u Mletke. Za nagradu bude mu padovanska profesura proglašena doživotnom, a plaća mu podvostručena. Galilei je prvi d-om sustavno pretražio nebo i pri tome otkrio niz znamenitih astronomskih činjenica; a dotjerao je taj »holandijski« d. toliko, da je vrlo razumljivo, da se on danas obično zove Galilejevim imenom.
Iz različitih podataka, koji potječu iz 16. st., može se zaključiti, da je krajem toga stoljeća izum d-a bio dozreo i da je tada taj izum i uspio. Da je on kroz razmjerno dugo vrijeme ostao tajnom, može se pripisati tome, što u ono doba pravo izumiočevo nije bilo zaštićeno, te je izumilac bio upućen, da drži tajnu, dok ne iskoristi izuma, a kako su prvi d-i bili namijenjeni samo vojničkoj upotrebi, sigurno se i s te strane tražila tajnost. G. 1906 saopćio je de Waard jednu holandijsku bilješku, koju je g. 1634 napisao prijatelj Descartesov Isaac Beeckman, koji se poput mnogih drugih ljudi onoga doba amaterski bavio brušenjem optičkoga stakla. U toj bilješci kaže Beeckman, da mu je Johannes Janssen, sin tobožnjeg izumioca Zachariasa Janssena, izjavio, »da je njegov otac prvi načinio d. u ovoj zemlji g. 1604 prema jednom d-u nekog Talijana, na kojemu je pisalo: anno 1(5)90«. Spram toga svjedočanstva ne zaslužuje vjere mnogo novija tvrdnja istoga Johannesa Janssena iz g. 1655, da je njegov otac izumio d. g. 1590; Zachariasu bile su tada možda tek dvije godine! Da prvi d. nije nastao u Holandiji, izlazi i iz jednog izvještaja, što ga je francuskom kralju Henriku IV. upravio njegov poslanik u Holandiji Jeannin, koji se mnogo zanimao za ratne izume. U tom se izvještaju spominje d. kao »nanovo izumljen u ovoj zemlji«.
Danjon i Coudé drže, da je Talijan, koji je izumio d., bio Giambattista della Porta, pisac glasovitog nekoć djela »Magia naturalis« (1589). O njemu se već iz g. 1580 sačuvala vijest, da je u Muranu (kod Mletaka) bio zabavljen »pravljenjem sprava za gledanje u daljinu« i da »nije htio pokazati svoje tajne baš nikomu«. On sam već g. 1586 piše kardinalu d’Este, da umije »praviti naočale, koje dopuštaju prepoznati čovjeka udaljenog nekoliko milja«. Uostalom, Porta je već g. 1558 stavio leću u prošireni otvor »tamne izbe« (→ camera obscura) i isporedio oko s tim preinačenim aparatom, te mu je djelovanje leća bilo — s obzirom na tadašnje znanje — bez sumnje dobro poznato.
Ako Keplerov d. isporedimo s Galilejevim u pogledu tumačenja njihova djelovanja, opažamo, da nam je Keplerov u prvi mah lakše shvatljiv: treba naprosto Portinu komoru sastaviti s lećom, koja povećava bližnje sitne predmete, a to je zbirna leća. Kako je ipak Galilejev d. prvi izumljen, očito je, da je taj izum plod pokusa. To, što je Galilejev d. kraći, doista čini vjerojatnim, da je ta sprava bila prije izumljena nego li dulji, Keplerov d. Povrh toga činjenica, da Keplerov d. pokazuje predmete obrnuto, u prvi mah prikazuje taj d. bezvrijednim, te je jamačno i zbog toga sastavljanje toga d-a zakasnilo.
Kepler nije načinio d-a, koji je opisao (g. 1611, u djelu Dioptrice XXCVI). Sastavio ga je tekar isusovac Scheiner g. 1613. Kepler je uputio još i na to, da se umetanjem leće može njegov d. tako preinačiti, da pokazuje uspravno. Takav terestrički d., t. j. za motrenje zemaljskih predmeta (lat. terra »zemlja«) sagradio je g. 1645 Schyrl, opat samostana Rheidt (Schyrlaeus de Rheidta). Takav je d. onda dulji nego li Keplerov jednakog objektiva i povećanja, a pogotovu dulji od Galilejeva. Sl. 4b na tab. II. prikazuje isti d. kao i sl. 4a na tab. II., ali s terestričkim okularom.
Već je Galilei s povećavanjem išao do krajnjih granica unutar kojih su se njegovim d-ima predmeti vidjeli još iole dobro. Kada se našlo, da je sferna aberacija to manja što su površine leća manje zakrivljene, počeli su graditi d-e sa sve slabijim objektivima, t. j. sve većim žarišnim daljinama F. Dalekozori postajali su sve dulji, te su dugački refraktori značajni za konac 17. i početak 18. stoljeća. Tako je Bradley g. 1722 mjerio promjer planeta Venere dalekozorom, kojemu je objektiv imao žarišnu daljinu od 212 stopa. Ti dugački d-i nisu imali cijevi, da ne budu preteški, a kod najduljih uopće nije bilo mehaničke sveze između objektiva, koji se u visini zasebno namještao prema zvijezdi, i okulara, s kojim se motrilac morao pomicati, da mu zvijezda ostane u vidnom polju. Rad s takvim uzdušnim d-ima bio je vrlo tegotan i iziskivao je mnogo spretnosti. Njihovo je doba prestalo uvođenjem d-a reflektora i usavršavanjem objektiva.
 Sl. 10. Put svjetlosti u Porrovu dalekozoru
Sl. 10. Put svjetlosti u Porrovu dalekozoru Sl. 11. Dalekozor s prizmama
Sl. 11. Dalekozor s prizmama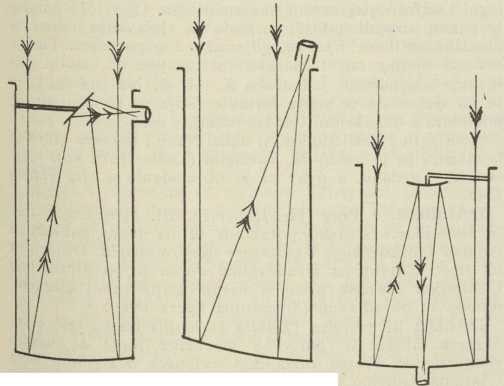 Sl. 12. Reflektori
Sl. 12. Reflektori
a) Newtonov, b) Herschelov,
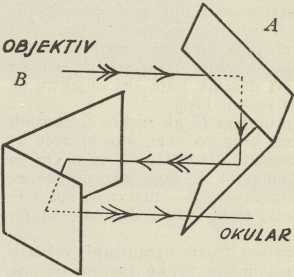
c) CassegrainovDalekozori s prizmama. G. 1850 pokazao je Porro, kako se može bez pomoći treće leće udesiti, da Keplerov d. pokazuje uspravno: između objektiva i okulara stave se u put zrakama svjetlosti dvije prizme, u kojima se svjetlost tako odbija, da se slika u žarišnoj ravnini objektiva okrene, te postane uspravna.
Zamislimo umjesto jedne Porrove prizme dva zrcala A (sl. 10), koja se sastaju u jednoj stranici i priklonjena su jedno spram drugoga za 90°. Ako je zajednička stranica vodoravna i ako gledamo u kut njihov, vidimo svoj lik obrnut u smjeru gore-dolje. Pojav taj nastaje time, što se svjetlost odbije na jednom zrcalu, onda udari na drugo, na njemu odbije i pođe smjerom natrag. Zamislimo dalje, da taj par zrcala stoji na putu zrakama, što dolaze od objektiva, a iza obiju refleksija na tim zrcalima neka svjetlost pogodi drugi, jednaki par zrcala B, kojima zajednička stranica stoji vertikalno. Kada se svjetlost i na zrcalima B odbila, pođe ona opet naprijed, prema okularu. Kako zrcala A okreću sliku smjerom gore-dolje, tako je zrcala B okreću smjerom vodoravnim, te se slika najposlije iza ove četiri refleksije okrene u svima smjerovima. To je osnovna misao Porrova d-a. Međutim, odbijanjem na zrcalima izgubilo bi se mnogo svjetlosti; zato se mjesto svakoga para zrcala uzme po jedna trostrana optička prizma (sl. 11). Svjetlost ulazi u prizmu kroz njezinu hipotenuznu (širu) površinu, onda se redom odbija na katetnim površinama kao na prije zamišljenim zrcalima, te izađe kroz hipotenuznu površinu iz prizme. Radi se o t. zv. potpunoj ili totalnoj refleksiji, te su gubitci svjetlosti, koji nastaju umetanjem tih prizama, neznatni.
Sl. 11. prikazuje dvostruk (binokularan) Porrov d. Već se izvana razabire njegovo značajno svojstvo, da je os okulara spram osi objektiva usporedno pomaknuta. Još vidimo ove osobitosti toga d-a. Razmak okulara dade se mijenjati, što je učinjeno, jer je razmak očiju u različitih ljudi različit. Okular svakog pojedinačnog d-a u toj spravi dade se napose udesiti prema oku, s obzirom na to, što vid u oba oka čovječja nije vazda jednak. Razmak osi objektiva veći je od razmaka osi okulara, što se kazališnim staklom, sastavljenim iz Galilejevih dalekozora, ne da postići, a dopušta nam, da vidimo prostorno ili plastično u veće da ljine nego li bez stakla. Sposobnost prostornog gledanja zahvaljujemo tome, što gledamo sa dva oka, i ona je to veća, što su oči više razmaknute. Povećani razmak objektiva znači dakle isto kao da su oči više razmaknute. Najposlije, prizme u sl. 11. nisu blizu jedna drugoj, nego je jedna bliže objektivu, druga bliže okularu; uslijed toga prelomljeni je put zrake od objektiva do okulara razmjerno dugačak, premda okular nije daleko od objektiva, te sam d. nije dug.
Značajno je, kako su tek postepeno uvedene sve prednosti, koje su se mogle crpsti iz Porrova izuma. Tako je tekar Boulanger g. 1859 uzeo patent na binokularni d. s Porrovim prizmama, premda je već Lipperhey gradio binokularne d-e; pri tome, međutim, nije pazio, da razmak objektiva bude veći. U tom je pogledu tekar Abbe tu spravu dotjerao. Abbe je također spravu skratio, naime time, što je prizme rastavio, dok ih je Porro smještao jednu tik druge.
Ima i drugih načina, kako se slika u Keplerovu d-u uspravlja potpunim refleksijama u zgodno građenim prizmama, pa i takvih, gdje se os okulara i os objektiva podudaraju.
Zrcalni dalekozor ili reflektor. Poput zbirne leće stvara slike i ugnuto ili konkavno zrcalo. Na tom se osniva građenje d-a, u kojima se leća objektiva Keplerova d-a nadomješta ugnutim zrcalom. Takav d. reflektor ima okular kao i Keplerov d. Ako taj d. upravimo na udaljen predmet, zrake svjetlosti, udarajući o zrcalo, na njem se odbijaju i onda načine sliku predmeta u žarišnoj ravnini zrcala; ta je ravnina okomita na osi zrcala i presijeca os u žarištu, a udaljena je od zrcala za dužinu F, koja se zove žarišna daljina zrcala; središte krivosti zrcala dvaput je dalje, t. j. udaljeno je za 2F. Kako kod leće pravac, koji spaja svijetlu točku i njezinu sliku, ide kroz sredinu leće, tako kod ugnutog zrcala taj pravac ide središtem krivosti zrcala. Otuda se iako vidi, da je i ovdje slika to veća, što je veće F, t. j., što je zrcalo manje ugnuto.
Bitna je razlika prema djelovanju leće, da ovdje slika nastaje na istoj strani, na kojoj se i predmet nalazi, pa je u tom znatna teškoća za sastavljanje toga instrumenta, jer kada bismo htjeli motriti sliku, koju zrcalo načini, onako kao kod Keplerova d-a, zastrli bismo glavom svjetlost. Najjednostavnije se ta teškoća obilazi kod Herschelova reflektora (sl. 12b), naime tako, da se zrcalo ponešto nagne, te mu središte krivosti ne stoji u osi d-a. Svjetlost dakle pada ponešto koso na zrcalo, pa se i koso odbija, te je hvatamo okularom, koji se nalazi postrance, blizu gornjega, prema predmetu (zvijezdi) okrenutoga ruba d-ova. Radi kosog dolaženja zraka znatna je aberacija, poimence koma i astigmatizam (→ aberacija, 2). Drukčiji je uređaj Newtonova reflektora (sl. 12a), gdje se između ugnutog zrcala i njegova žarišta, a blizu žarišta, stavlja maleno ravno zrcalo, koje je priklonjeno prema osi zrcala za kojih 45°. Svjetlost, koja se odbila na ugnutom zrcalu, ravnim se zrcalom baca na stranu, načini sliku, i slika se motri okularom, koji je upravljen prema osi d-a. Ravno zrcalo i njegov držak ne zastiru mnogo svjetlosti. Treći, danas najobičniji način građenja reflektora, zamislio je Cassegrain. U njegovu d-u (sl. 12c) konkavno zrcalo ima u sredini okruglu rupu. Njemu nasuprot stoji u primjerenoj daljini manje, pomoćno zrcalo, koje je pupčasto ili konveksno. Iza refleksije na glavnom zrcalu svjetlost zgađa pomoćno zrcalo i od njega se refleksijom navraća prema sredini glavnog zrcala, u kojega blizini združenim djelovanjem glavnog i pomoćnog zrcala nastaje slika. Tu sliku motrimo okularom smještenim iza glavnog zrcala. Kod Newtonova i Herschelova reflektora oko se nalazi blizu onom kraju d-a, koji je okrenut k predmetu, kod Cassegrainova ono je na protivnoj strani, a to je kod velikih instrumenata značajna razlika. Uostalom, danas se te sprave često tako grade, da se glavno zrcalo dade upotrijebiti na više načina, u Newtonovu ili u Cassegrainovu sastavu ili u kojem drugom, u novije vrijeme predloženom. Kada se fotografira, onda gdjekada stavljaju fotografsku ploču naprosto u žarišnu ravninu ugnutoga zrcala.
Jedna prednost zrcalnoga d-a pred refraktorom u prvi je mah očita. On je bez kromatičke aberacije: zrake svjetlosti različitih boja jednako se odbijaju, pa je za djelovanje zrcala svejedno, koja je boja svjetlosti. Poradi toga, dok se nije znalo, kako se kod leća može ukloniti kromatična aberacija ili se čak mislilo, da to nije moguće, sve su se nade u pogledu napretka d-a stavljale u reflektore.
Što se tiče oblika površine ugnutog zrcala reflektora, daleko je najjednostavnije, da se ta površina uzimlje kuglasta ili sferna, pa su se tako prije vazda ta zrcala i brusila. Međutim, od starine poznato svojstvo krivulje parabole upućivalo je na to, da bi bilo dobro, da se ugnuto zrcalo ne načini sferno nego u obliku dijela plohe rotacionoga paraboloida, t. j. plohe, koja nastaje, kada se parabola vrti oko svoje osi. T. zv. vrh paraboloida je onda sredina zrcala. Svjetlost, naime, koja dolazi na takvo zrcalo usporedno s osi njegovom, poslije refleksije sastaje se točno u žarištu, tako da za tu najznatniju točku slike nema sferne aberacije. Sferno se zrcalo ne odlikuje tim svojstvom. Isto tako upućuju svojstva hiperbole, da se pomoćno zrcalo Cassegrainova d-a načini u obliku komada plohe rotacionoga hiperboloida, plohe, koja nastaje vrtnjom hiperbole oko njezine glavne osi. Doista se danas zrcala najvećih reflektora prave prema tima zahtjevima. Nekoć su se zrcala za reflektore pravila iz kovine, danas se prave iz stakla. Ako je zrcalo iz stakla, treba mu prednju stranu prevući slojem kovine, te se ono na pr. posrebruje ili — u najnovije vrijeme — pokrije aluminijskim slojem, jer taj jače odbija ultraljubičaste zrake, važne pri fotografiranju, a i trajniji je, te ga ne treba tako često obnavljati.
 Sl. 13. Paraboloidno zrcalo
Sl. 13. Paraboloidno zrcalo
s promjerom 100 palacaSl. 13. prikazuje paraboloidno zrcalo najvećega današnjega zrcalnog d-a (sl. 1. na tab. I.), postavljenoga g. 1917 na Mt. Wilsonu u Kaliforniji. Promjer toga zrcala jest 257 cm (»100 palaca«!), F = 12,9 m. Širina je toga zrcala dakle 2½ put veća nego li promjer leće najvećega refraktora, te je i omjer otvora veći i jednak 1 : 5. Dugo je već u gradnji reflektor za zvjezdarnicu na Mt. Palomar, također u Kaliforniji. Njegovo glavno zrcalo ima promjer od 200 palaca, a načinjeno je iz osobitog pyrex-stakla (s mnogo kvarca), koje kod promjene temperature manje mijenja oblik nego li do sada uobičajena stakla. Da ne bude to zrcalo predebelo i preteško, ono je naneseno kao sloj na jednoj rebrastoj čeličnoj podlozi.
Zrcalni d-i odlikuju se obiljem svjetlosti, ali im je vidno polje neznatno, budući da već iole većim udaljivanjem iz smjera osi d-ove aberacije postaju velike, slika loša. Kod vizualnog opažanja to ne treba mnogo smetati, jer se može zakretanjem d-a predmet dovesti u sredinu vidnog polja, gdje ga vidimo valjano. Smetnja je međutim kod fotografiranja. Među različnim suvremenim nastojanjima, da se reflektori usavrše, treba spomenuti izum B. Schmidta u Hamburgu, koji je g. 1931 pokazao, kako se mogu graditi reflektori sa širokim vidnim poljem, a bez znatnih pogrešaka aberacije. Radi se o kraćim d-ima, s velikim promjerom zrcala, a zrcalo nije paraboloidno nego sferno, što je jednostavnije i jevtinije. Na mjestu, gdje je središte krivosti zrcala, t. j. u daljini 2F od zrcala, namješta se zaslon s okruglim otvorom, koji ima manji promjer nego li zrcalo. Time se suzuju svežnjevi svjetlosti, koji padaju na zrcalo, tako da pri stvaranju slike nekog prostranog nebeskog predmeta za svaku točku njegovu pretežu zrake, koje idu kroz središte krivosti. Slika je, doduše, onda zaobljena, jer je rasprostrta u kugli, koja je koncentrična sa zrcalom, a prolazi kroz žarište, ali je slobodna od kome i astigmatizma. Da se i ostatak aberacija ukloni, stavlja se u spomenuti otvor staklena »korekciona ploča«. Ta ploča ima jednu površinu, koja nije kuglasta, a dobiva se osobitim postupkom: za vrijeme brušenja ploča stoji s jedne strane pod tlakom zraka, dok drugom graniči na zrakoprazni prostor. Izobličenje ploče, koje se time dobiva, baš je takvo, da ploča popravlja ostatak pogrešaka konkavnog zrcala. Najveći Schmidtov dalekozor izrađuje se sada u Americi za zvjezdarnicu na Mt. Palomar; njegovo zrcalo ima promjer 180 cm, korekciona ploča 120 cm, pa kako je žarišna daljina 3 m, izlazi za taj reflektor velik omjer otvora 120 : 300 = 1 : 2∙5.
Zamisao d-a reflektora naskoro je nikla, pošto su načinjeni prvi holandijski d-i. Tako su Marsili i Galilei raspravljajući o tom g. 1626 bili na čistu, da je takav d. moguć i da za nj treba osim ugnutog zrcala još i leća (okular). Sam Galilei nije iskušao tu stvar, jer nije mogao dobiti konkavnog zrcala. Zucchi opisuje g. 1652 takav d., što ga je načinio uzevši za okular rastresnu leću; iz njegova opisa izlazi, da je radio s kosim zrakama kao i Herschel. Reflektore sa dva zrcala predlagao je već g. 1636 Mersenne, ali je tekar Gregory g. 1663 potanje raspravio taj predmet i postavio zahtjev, da glavno zrcalo bude paraboloidno, a pomoćno ugnuto i elipsoidno.
Prvu dobru izvedbu reflektora zahvaljujemo Newtonu, koji je g. 1672 akademiji Royal Society predložio d. reflektor, kojemu je zrcalo s promjerom 37 mm i žarišnom daljinom 16 cm sam izbrusio. Povećanje je bilo 38-struko, a d. je pokazivao tako dobro kao tadašnji refraktori sa žarišnom daljinom 4 stope. Malo kasnije iste godine iznio je Cassegrain (u Chartresu), čiji se identitet ne da više odrediti, prijedlog za d., koji se danas — prozvan njegovim imenom — toliko cijeni. Zanimljivo je, da su i Newton i Huygens taj prijedlog kao loš najodlučnije odbili.
Kroz pola vijeka nitko nije Newtona dostigao u pravljenju zrcala, pa je tekar Hadley u građenju zrcalnih d-a učinio napredak. Međutim »slavu reflektora« stvorio je svojim astronomskim istraživanjima W. Herschel, koji je također sam brusio potrebna zrcala, te mu je najveći d. — iz g. 1789 — imao promjer zrcala 4 stope, a F = 40 stopa. U očima širih krugova reflektor je postao d-om kat’ eksohen, čemu nalazimo značajan odraz u francuskom jeziku, gdje riječ télescope znači baš samo d. reflektor. U drugoj poli prošloga vijeka ta se vrst d-a opet manje cijenila. Nov njihov procvat donosi naše vrijeme, koje suvremenim velikim reflektorima, u prvom redu onom od 100 palaca, zahvaljuje nove prodore u dubljine Svemira.
Vertikalni i horizontalni dalekozor. Ako astronomskom d-u želimo dodati spektralni uređaj velike rastvorne snage, naročito pri istraživanju Sunca, obični, pomični d. ne bi mogao tog uređaja nositi, zbog njegove veličine i težine. Zato je sagrađeno nekoliko d-a, većinom refraktora, kojima je os čvrsta i vertikalna ili vodoravna. Vertikalni se d. zove također toranj-d. Svjetlost se u te d-e navraća s pomoću celostata (lat. caelum »nebo«, stare »stajati«), dvaju zrcala, koja se tako pomiču, da prate nebesko tijelo u njegovu gibanju. Sl. 3. na tab. II. pokazuje celostat Potsdamskog toranjd-a; celostat je neposredno iznad objektiva. Toranj-d. na Mt. Wilsonu visok je 50 m (sl. 2. na tab. II.), njegov objektiv, širok 30 cm, stvara sliku sunčanu, kojoj je promjer 43 cm. Ispod tornja pod zemljom je rov, dubok 25 m, u kojemu je spektralni uređaj.
 DVOSTRUKI REFRAKTOR ASTROFIZIKALNOG OPSERVATORIJA
DVOSTRUKI REFRAKTOR ASTROFIZIKALNOG OPSERVATORIJA
U POTSDAMU.
Objektivi imadu promjere 80 cm (za motrenje)
i 50 cm (za fotografiranje).
(Henseling, Der neu entdeckte Himmel). Sl. 2. TORAN-DALEKOZOR OPSERVATORIJA
Sl. 2. TORAN-DALEKOZOR OPSERVATORIJA
CARNEGIEJEVA ZAVODA NA MT. WILSONU.
Na vrhu tornja nalazi se
objektiv i iznad njega celostat;
žarišna daljina objektiva 45∙75 c,
(Handbuch der Astrophysik).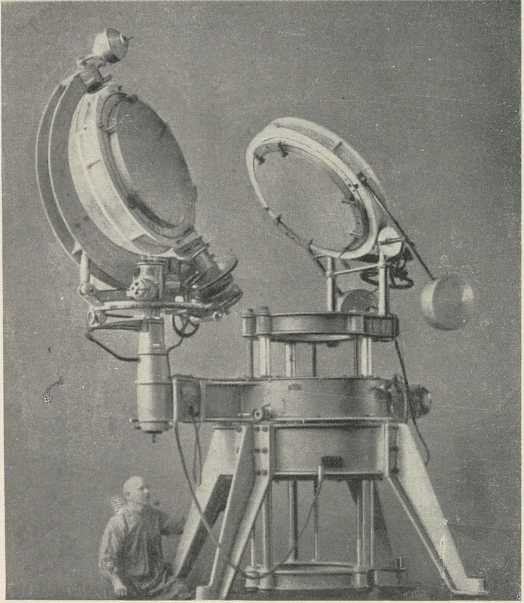 Sl. 3. CELOSTAT TORAN-DALEKOZORA
Sl. 3. CELOSTAT TORAN-DALEKOZORA
ASTROFIZIKALNOG ZAVODA U POTSDAMU.
Dva zrcala od kojih se jedno urom pomiče,
navraćaju svjetlost zvijezde prema dolje,
u objektiv vertikalnog dalekozora.
(Handbuch der Astrophysik).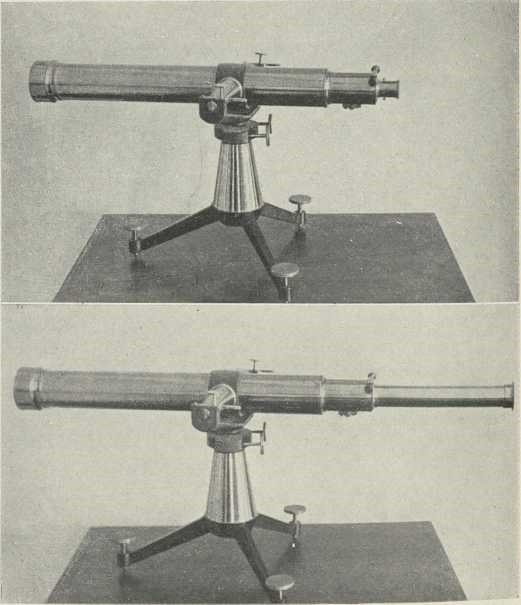 Sl. 4a. MALEN KEPLEROV DALEKOZOR:
Sl. 4a. MALEN KEPLEROV DALEKOZOR:
Pokazuje predmete obrnuto.
Sl. 4b.MALEN KEPLEROV DALEKOZOR (kao u 4a)
S TERESTRIČKIM OKULAROM.
Pokazuje predmete uspravno.LIT.: A. Danjon-A. Couder, Lunettes et télescopes, Pariz 1935; von Hofe, Fernoptik, 3. izd., Leipzig 1941; von Krudy, Das moderne Spiegelteleskop in der Astronomie, Leipzig 1919.St. H.