To su metode, kako da se ma koji broj predoči s pomoću nekih osnovnih znakova, t. zv. brojaka (v.) ili cifra. Već prema tome, radi li se o broju kao riječi, predmetu ili simbolu, imamo i tri vrste br. sustava: u riječi, materijalu i simbolu.
1. Pisani indijsko-arapski brojni sustav. Tu se na određen način (→ razlomak) svaki broj može predočiti s pomoću 10 brojaka: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 (koje po redu znače: ništa ili nulu, jedan, dva, tri, četiri, pet, šest, sedam, osam i devet) i osnovnih jedinica 1, 10, 102, 103,..., te 10-1 = 1/10’ 10-2<znak> 1/102’.... Evo glavnih svojstava toga sustava:
a) on je dekadski, t. j. baza mu je deset: ima 10 brojaka;
b) on je pozicioni: vrijednost brojke u simbolu zadana broja zavisi o njezinu položaju u tom simbolu; na pr. prvi 5 u 55 znači 5.10, dok drugi 5 znači 5.1; c) on zadovoljava Hankelovu principu redosljeda: brojke za jedinice višega reda nalaze se ispred brojaka za jedinice nižega reda, na pr. 54 znači 5.10+4, a ne 5+4.10; d) on je aditivno-multiplikativan: broj se dobiva iz osnovnih jedinica zbrajanjem i množenjem, na pr. 540,07 = 5∙102+4∙10+0∙1+0∙10-1+7∙10-2; e) on ima poseban znak, 0, za broj nula (ovo je svojstvo jedna od najvažnijih tekovina u matematici: ono je omogućilo razvitak matematike i njezine primjene); bez 0 ne bismo znali razlikovati brojeve 23; 203; 2000300 i t. d. (slučaj sumersko-babilonskoga pozicionog br. sustava s bazom 60).
Historijat. Taj se sustav razvio u Indiji, i to po svoj prilici iz računanja na abaku, posutu pijeskom ili prašinom (ovo to prije, što u sanskrtu ima nezavisnih posebnih riječi za sve potencije 10, 10
2, 10
3, ..., 10
9, 10
10); u 5. st. već je izgrađen tako, da ga na pr. Ariabhata (5. st.), Brahmagupta (6. st.) uopće ne tumače u svojim djelima smatrajući ga opće poznatim. Bitna mu je oznaka, da ima 0 (→
brojka). U Siriji se spominje 666 (biskup Sabokht). Arapi su ga primili u 7. i 8. st. i raširili po zapadnom kršćanskom svijetu. Prvu arapsku matematiku u indijskom sustavu napisao je u 8. st. al-Khowârizmî ili Alkvarazmi, a Adelard iz Batha preveo ju je oko 1120 na latinski pod imenom
Liber algoritmi de numero Indorum, prema čemu u 12. st. riječ algoritam (v.) znači računanje u indijskom br. sustavu.
Liber abaci (1202) od Leonarda iz Pize pisana je u ind.-arap. br. sustavu. U 15. st. taj je sustav već istisnuo rimski br. sustav; otada je on velika tekovina čovječanstva (→
algoritam).
2. Gotovo svaki narod ima svoj posebni govoreni br. sustav; brojke našega govorenoga sustava jesu: ništa, jedan, dva, tri četiri, pet, šest, sedam, osam, devet, deset, sto ili stotina, hiljada ili tisuća, milijun i miljarda; on je multiplikativno-aditivan, zadovoljava Hankelov princip osim za brojeve 11, 12,..., 19 (na pr. petnaest = pet nad deset mjesto deset i pet).
3.
Brojni sustavi u materijalu danas se manje upotrebljavaju; u najstarije doba prsti su bili takav sustav (računanje prstima!), poslije su došli abaki (v.). »Brojke« su bile vrlo raznolične: kamenčići, kuglice, trstika, uzlovi, razne figure, a u 11. i 12. st. i posebno izrađene ind.-arapske brojke 1, 2,..., 9 (bez 0!) zvane apices (→
abak).
4. Gotovo svaki narod na višem stupnju razvoja stvorio je neki pisani br. sustav, no danas se čovječanstvo služi gotovo isključivo indijsko-arapskim. Gotovo svi poznati pisani br. sustavi zadovoljavaju Hankelov princip redosljeda, primitivniji su aditivni, a razvijeniji većinom multiplikativno-aditivni. Egipćani su imali dva adit. sustava: hijeroglifski (oko 3400 pr. Kr.) i hijeratski (Ahmesova računica pisana je u ovom) sa znacima za 1, 2,.., 9, 10, 20,.., 90, 100; na pr.
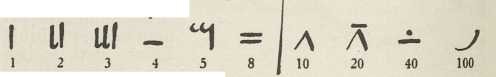
dakle:
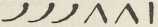
znači 321. Babilonci (klinasto pismo!) imali su mult.-aditivni sustav sa znacima:
Kad se manji znak napiše ispred većega, njihove se vrijednosti množe (kod Etruščana i Rimljana odbijaju, na pr. XL = L—X = 40). Sumerani su imali pozicioni sustav s bazom 60, ali nijesu imali nule; na pr.
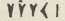
= 3.60
2+10.60+1.
Grci su imali dotjeran adit. sustav: po jednom su početna slova riječi za broj igrala uloge brojke, na pr. Π=5 (IIENTE), <znak>= 10 (<znak>EKA), H = 100 (HEKATON), X=1000 (XLIIOI), M = 1000 (MYPIOI); kasnije se uveo alfabetski sustav, i to ovako:
Hiljadu su naznačivali potezom s lijeve strane, na pr. /A = 1000, /I = 10000 i t. d. Analogan su sustav imali Hebreji služeći se hebrejskim slovima na pr. א=l.
Etruščani su imali dekadski sustav (proizišao iz kvinarnog) sa znakovima:
Preuzeli su ga Rimljani i preudesili za pisanje s lijeva na desno. Rimljani su broj a množili s 1000 ovako: (a) ili ā; na pr. ( | ) = 1000 (odatle prepisivanjem i iskrivljivanjem: M za 1000 i |) =D za 500 kao za polovicu hiljade. Kinezi su imali mult.-aditivni sustav s dvije vrste brojaka.
LIT.: M. Cantor, Vorlesungen über d. Geschichte der Mathematik, I. sv., Leipzig 1894; E. Löffler, Ziffern und Ziffernsysteme der Kulturvölker, Leipzig-Berlin 1912.