DIFERENCIJALNE JEDNADŽBE. Već od prvih početaka diferencijalnoga i integralnoga računa prirodno su se javile diferencijalne jednadžbe u istraživanjima matematika. Znameniti onaj »obrnuti problem tangente« (→ Diferencijalni račun), koji traži, da se iz poznatih svojstava tangente krivulje odredi i sama krivulja, vodi do diferencijalne jednadžbe. Jer ako je a kut, što ga čini tangenta tražene krivulje u točki (x,y) s pozitivnom osi X, a y'(x) je derivacija tražene funkcije y(x) u istoj točki, to je y'(x) = tga; propisano svojstvo tangente bit će dakle predočeno zadanom nekom vezom između derivacije i koordinata točke. Postojat će prema tome jednadžba oblika y'(x) = f(x,y), u kome je derivacija predočena u eksplicitnoj zavisnosti o koordinatama točke, ili oblika F(x,y,y') = 0, koji predočuje tu vezu u implicitnom obliku, i od kojih su oba »diferencijalne jednadžbe« tražene funkcije y(x).
1. Razdioba diferencijalnih jednadžbi. Pod diferencijalnom jednadžbom razumijeva se uopće kojagod veza, algebarska ili transcendentna, između nezavisne promjenljive, jedne ili više njih, funkcija tih promjenljivih i derivacija tih funkcija po nezavisnim promjenljivima. Ako u izraz, koji predočuje tu vezu, ulazi jedna funkcija y(x) samo jedne promjenljive x i njene derivacije y'(x), y"(x),..., jednadžba je obična; ako funkcija zavisi o dvije ili više promjenljivih, diferencijalna jednadžba je parcijalna, jer su i derivacije funkcije po promjenljivima x i y samo parcijalne (Dif. rač.). Diferencijalna jednadžba je n-toga reda, ako je najviša derivacija, koja ulazi u izraz, n-toga reda; ona je m-toga stupnja, ako najviša derivacija, koju jednadžba sadržava, pošto je uređena, dolazi u m-toj potenciji. Tako je na pr. jednadžba
(1 ∙ 1)y" + a2y = 0
obična diferencijalna jednadžba drugoga reda (n = 2) i prvog stupnja (m — 1), a
(1 ∙ 2) y2 + y'2 = 2x—1
obična jednadžba prvoga reda (n = 1) i drugog stupnja (m = 2);
napokon je (1 ∙ 3)δ2V/δx2 + δ2V/δy2 + δ2V/δz2 = 0
parcijalna diferencijalna jednadžba drugoga reda u tri promjenljive. Ako tražene funkcije i sve njihove derivacije dolaze samo u prvoj potenciji, diferencijalna jednadžba je linearna; na pr. jednadžbe (1 ∙ 1) i (1 ∙ 3) su linearne, a (l ∙ 2) nije. Diferencijalnu jednadžbu riješiti ili integrirati (u širem smislu, → Int. račun) znači naći funkciju (ili funkcije), koja, uvrštena u jednadžbu, identički je zadovoljava. Svaka funkcija, koja zadovoljava diferencijalnu jednadžbu, zove se rješenje njeno ili i integral (u širem smislu). Tako je na pr. funkcija y=sinax rješenje jednadžbe (1 ∙ 1), jer je y"= —a2sinax, dakle je y" + a2y = —a2sinax + a2sinax=0.
2. Najjednostavnija obična diferencijalna jednadžba 1. reda je
(2 ∙ 1) dy/dx =f(x),
gdje je f (x) zadana funkcija od x. U integralnom se računu (v.) pokazuje, da je najopćenitija funkcija, koja zadovoljava tu jednadžbu, neodređeni integral
(2 ∙ 2) y (x) = ʃ f (x) dx + C,
gdje je C konstanta po volji. Tako je na pr. najopćenitije rješenje jednadžbe
dy/dx = 2x
funkcija y(x) = x2 + C, jer je derivacija te funkcije 2x, ma kakovu vrijednost imala konstanta C, i jer nema druge funkcije s istom derivacijom. Svaka, dakle, od funkcija x2, x2 — 1, x2 + √ 3 i t. d. zadovoljava tu jednadžbu; sve one izlaze iz rješenja y = x2 dodavanjem konstanata po volji. Jer y = x2 predočuje u pravokutnom koordinatnom sustavu XOY parabolu, koja prolazi ishodištem, a os joj pada u os Y sustava, predočuje svako od tih rješenja parabolu sukladnu s prvom, samo pomaknutu usporedno duž osi Y za dužinu C = —1, + √ 3 i t. d. Slično predočuje jednadžba (2 ∙ 2) za svaku posebnu vrijednost konstante C jednu krivulju u ravnini, a za općenito C skup svih tih pojedinih krivulja. Stoga se (2 ∙ 2) i zove opće rješenje diferencijalne jednadžbe (2 ∙ 1), a izrazi, koji iz njega izlaze za posebne vrijednosti konstante C (C = —1, + √ 3 ,...), partikularna ili posebna rješenja. Ti se izrazi prenose i na opću jednadžbu 1. reda.
3. Diferencijalne jednadžbe prvoga reda. Prve primjene diferencijalnoga računa na probleme geometrije i mehanike dovele su do nekoliko jednostavnih jednadžbi 1. reda, od kojih ćemo navesti glavnije.
a) Jednadžbe s odijeljenim promjenljivima su oblika
dy/dx = f1(x)/f2(y) ili f1 (x) dx = f2(y) dy;
f1 i f2 su zadane funkcije, od kojih svaka zavisi samo o jednoj promjenljivoj x ili y. Budući da su diferencijali na obje strane jednaki, mogu se obje strane razlikovati samo za jednu konstantu (Dif. rač.); dakle je najopćenitije rješenje, koje zadovoljava tu jednadžbu, dano u obliku
ʃf1(x)dx = ʃf2(y)dy + C,
gdje je C konstanta po volji. Kad je rješenje diferencijalne jednadžbe, kao u ovom slučaju, svedeno na određivanje neodređena integrala, kaže se, da se jednadžba rješava kvadraturom. Taj se oblik javlja na pr., kada se traže sve krivulje u ravnini, kojima je subnormala (Dif. rač.) konstantna. Budući da je izraz za subnormalu jednak yy', vodi taj problem do jednadžbe
y dy/dx = a
gdje je a zadana konstanta, ili do
y dy= a dx,
u kojoj su promjenljive odijeljene. Opći integral, dakle, glasi
ʃydy = aʃdx + C,
ili, nakon izvedenih integracija,
1/2 y2 = ax + C, t. j. y2 = 2ax +2C.
Integralne su krivulje, dakle, parabole, kojima je os usporedna s osi X, a vrh se nalazi na osi Y u daljini √ 2C .
b) Homogene diferencijalne jednadžbe. Zadane su izrazom
dy/dx = f (y/x).
Ako se stavi y/x = u(x), t. j. ako se mjesto y(x) uvede y(x) = x ∙ u(x), bit će y' = x ∙ u' + u (Dif. rač.), a jednadžba prelazi u
x du/dx + u = f (u) ili du/f (u) − u = dx/x,
u kojoj su promjenljive odijeljene. Na pr. jednadžba dy/dx = y/x vodi tim načinom do x ∙ u' + u = u ili do x du/dx = 0, t. j. do du/dx = 0, koja izriče, da je u(x)=Const., da je dakle y/x = C ili y = C ∙ x opće rješenje.
c) Linearne diferencijalne jednadžbe prvoga reda. Prema definiciji i funkcija i derivacija dolaze u tim jednadžbama u prvoj potenciji, dakle su oblika
(c1) dy/dx + + f1(x)y + f2(x) =0,
gdje su koeficijenti f1 i f2 zadane funkcije od x. Da je integriramo, pođimo od jednostavnije linearne jednadžbe 1. reda, u kojoj je f2 = 0, t. j. od jednadžbe
y' + f1y = 0.
Budući da je y'/y = dlny/dx = —f1,(x), to je lny =—ʃf1(x)dx + lnC, gdje smo konstantu po volji pisali u obliku lnC, odakle slijedi
(c2) y(x) = Ce-g, g(x)=ʃf1(x)dx.
Da integriramo zadanu jednadžbu (c1), poslužimo se metodom varijacije konstanata, t. j. gledajmo, da se i rješenje jednadžbe (c1) predoči u obliku (c2), u koji se samo mjesto konstante C uvrštava zgodno odabrana funkcija C(x) promjenljive x, na što se i proteže ime te metode. Iz (c2) izlazi diferenciranjem
y'=e-g [C'(x)—C ∙ f1x)].
Ako to uvrstimo u (c1), preostaje samo uvjet
C'(x) ∙ e-g + f2(x) = 0, t. j. C'(x) =—f2(x) ∙ eg,
odakle se integracijom dobiva tražena funkcija od x
C(x) — C— ʃf2egSdx,
gdje je sada C konstanta po volji. Ako taj izraz uvrstimo u (c2), dobijemo opće rješenje jednadžbe (c1) u obliku
(c3) y(x) = e-g[C—ʃf2egdx],
dakle izraženo s dvije kvadrature. Na jednadžbu toga oblika nailazimo na pr. u problemu elektrotehnike, da se odredi u svaki čas t jakost I(t) izmjenične struje u vodu otpora R i vlastite indukcije L, koja teče radi elektromotorne sile E, koja je zadana funkcija vremena t. Budući da je
E = IR + L dl/dt treba I(t) odrediti dakle iz diferencijalne jednadžbe 1. reda dl/dt + R/L I — E/L = 0. Ako je E(t) = E0 sinωt, bit će prema (c3) opći integral
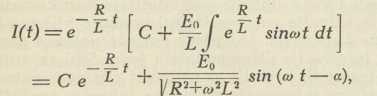
gdje je tg α = ωL/R (Int. račun).
d) Eksaktne diferencijalne jednadžbe. Uzmimo, da je jednadžba dana u obliku
P(x,y) + Q(x,y) ∙ y' = 0 ili P(x,y)dx + Q(x,y)dy = 0, (d1), u kome su P i Q zadane funkcije od x i y. Ako je lijeva strana jednadžbe (d1) totalni diferencijal (Dif. rač.), t. j. ako ima jedna funkcija od x i y, z(x,y), kojoj je totalni diferencijal dz = δz/δx dx + δz/δy dy jednak toj lijevoj strani, diferencijalna se jednadžba zove eksaktna i može se integrirati kvadraturama, jer tada (d1 nije drugo nego dz=0, iz čega izlazi z — Const. Uvjet za to je
δP/δy = δQ/δx
(Dif. rač.). Iz izraza za integral totalnoga diferencijala (Int. rač.) izlazi, da će opće rješenje imati oblik
z (x ,y) = ʃxx0P (x, y) dx + ʃ xx0Q (x0, y) dy + C,
gdje je opet C konstanta po volji. Takva je na pr. jednadžba xdx+ydy=0, u kojoj je P=x, Q=y, Py=Qx=0; opći je integral dakle
ʃxx0 x dx+ ʃyy0 y dy = C ili 1/2 x2 + 1/2 y2 — 1/2 (x20+y20) = C, pa je predočen geometrijski skupom koncentričnih kružnica sa središtem u ishodištu koordinatnoga sustava.
e) Eulerov multiplikator. Ako u jednadžbi Pdx+Qdy=0 izraz na lijevoj strani nije totalni diferencijal, može on to postati nakon množenja zgodno odabranom funkcijom μ(x,y); ako ima takva funkcija, to je
μ (Pdx + Qdy) = dz,
a μ(x,y) se zove multiplikator linearnog diferencijalnog izraza Pdx + Qdy. Tako na pr. izraz xdy — ydx, u kome je P=—y, Q=x, nije totalni diferencijal, jer nije ispunjen uvjet Py=Qx (Py=—1, Qx= + 1), ali postaje totalnim diferencijalom nakon množenja s 1/x2, jer je 1/x2 (xdy—ydx)= = d (y/x). Diferencijalna jednadžba xdy—ydx=0 ista je, dakle, kao d (y/x) =0, kojoj je rješenje y/x = C. Iz uvjeta za totalni diferencijal
δ (μP)/δy = δ (μQ)/δx
izlazi, da je multiplikator μ rješenje parcijalne diferencijalne jednadžbe 1. reda
Q δμ/δx — P δμ/δy + μ(Qx —Py) = 0.
Teorija tih jednadžbi pokazuje, da zadana diferencijalna jednadžba ima bezbroj multiplikatora, no dovoljno je znati samo jedno partikularno rješenje te parcijalne jednadžbe. U gornjem primjeru na pr. zavisi multiplikator samo o x, što olakšava traženje takvoga rješenja. Budući da se množenjem s μ(x,y), uz uvjet, da je μ(x,y)≠0, rješenja diferencijalne jednadžbe ne mijenjaju, bit će rješenje gornje jednadžbe oblika z(x,y) = C, gdje je funkcija z dana izrazom dobivenim u d).
f) Clairautova jednadžba. Zanimljiva je stoga, što se opće rješenje dobiva procesom diferenciranja, a ne integriranja. Ona je oblika
y = x dy/dx + f (dy/dx);
f je zadana funkcija od dy/dx. Ako stavimo dy/dx = p i jednadžbu diferenciramo po x, izlazi
p = dp/dx + p + f'(p) dp/dx ili dp/dx [x + f'(p)] = 0.
Dakle je ili dp/dx = 0, t. j. p = y' = Const., što uvršteno u diferencijalnu jednadžbu daje opći integral y(x)=Cx+f(C), koji pokazuje, da su integralne krivulje pravci u ravnini, kojima je gradijent C po volji, a odsječak na osi Y slijedi zakon f(C); ili je x + df(p)/dp = 0, no jer je izraz na lijevoj strani parcijalna derivacija po p zadane jednadžbe y = xp + f(p), dobiva se eliminacijom derivacije p iz zadane diferencijalne jednadžbe i ove posljednje neka jednadžba F(x,y)=0, koja predočuje krivulju u ravnini, što se zove envelopa (umotaljka) sustava pravaca y = Cx + f(C), jer ju svi pravci toga sustava diraju. Diferencijalna jednadžba može dakle izuzetno imati i rješenja, koja nisu sadržana u općem integralu; takva se rješenja zovu singularna.
To su neke glavnije vrsti diferencijalnih jednadžbi 1. reda, koje se mogu integrirati elementarno, t. j. s pomoću konačnoga broja t. zv. elementarnih funkcija (v.) i neodređenih integrala (kvadratura). Ako je zadana jednadžba izvan tih (i još nekih rijetkih) vrsti, preostaju za traženje rješenja još beskonačni procesi (na pr. beskonačni redovi) te približno numeričko izračunavanje ili i grafička integracija. Metode, kojima su osnivači više analize i njihovi nasljednici htjeli rješavati diferencijalne jednadžbe 1. reda, pokazuju se kod velike većine jednadžbi bezuspješnima. Razlog je tome, što su sredstva analize bila suviše oskudna, da bi mogla obuhvatiti svu onu nepreglednu raznoličnost funkcijskih veza, koje mogu biti sadržane u diferencijalnoj jednadžbi. Problem integracije diferencijalnih jednadžbi u tom smislu bio je, dakle, shvaćen s krive strane. Prvi, koji je sustavno udario novim putem u izučavanju diferencijalnih jednadžbi, bio je H. Poincaré; on je uvidio, da treba problem obrnuti i, mjesto nastojanja, da se jednadžba integrira elementarno, shvatiti obrnuto diferencijalnu jednadžbu samu u sebi kao predmet izučavanja i izvor novih funkcija, koje su njome definirane i kojih se svojstva moraju istom istražiti. Novi taj put u izučavanju diferencijalnih jednadžbi donio je važnih rezultata u teoriji jednadžbi nesamo prvoga reda, a napose je u mehanici neba postigao Poincaré u tom smislu sasvim nove spoznaje.
4. Geometrijska i mehanička interpretacija. a) Budući da je u diferencijalnoj jednadžbi 1. reda dy/dx = f(x,y) funkcija f(x,y) zadana, neprekinuta funkcija od x i y u nekom području ravnine (X,Y), propisuje ona u svakoj točki (x,y) toga područja smjer tangente tgα (Dif. rač.), t. j. smjer integralne krivulje, koja prolazi tom točkom. Takva jednadžba predočuje, dakle, geometrijski polje smjerova u ravnini. Integrirati diferencijalnu jednadžbu znači naći krivulje u ravnini (integralne krivulje), koje u svakoj točki, kojom prolaze, imaju smjer propisan diferencijalnom jednadžbom.
b) Ako je u ravnini zadano polje sila, t. j. ako je svakoj točki (x,y) nekoga područja ravnine pridijeljen vektor sile s komponentama X(x,y) i Y(x,y), silnice toga polja, t. j. krivulje, koje u svakoj točki, kojom prolaze, diraju vektor sile u toj točki, zadovoljavaju diferencijalnu jednadžbu 1. reda
dy/dx = Y (x,y)/X (x,y)
koja upravo izriče tu činjenicu; i obrnuto, svaka takva jednadžba može se shvatiti, da definira silnice jednoga polja sila, kome je komponenta X(x,y)=f(x,y), a Y(x,y) = 1.
5. Eksistencija rješenja diferencijalnih jednadžbi. Iz geometrijske interpretacije diferencijalne jednadžbe 1. reda već je vrlo vjerojatno, da će jedna integralna krivulja biti određena, ako zadamo točku (x0 ,y0 ) u ravnini, kojom mora prolaziti. Jer ako se malo pomaknemo iz te točke T0 po tangenti, propisanoj u toj točki, na pr. do točke T1, pa od točke T1 opet dalje po tangenti propisanoj u T1, i to nastavljamo, dobivamo slomljenu crtu, za koju se može očekivati, da će se sve više približavati traženoj integralnoj krivulji, koja prolazi točkom T0, što će pomaci na tangentama biti manji. Uz neke uvjete može se uistinu dokazati, da to vrijedi općenito. Uzmimo naime, da je u jednadžbi y' = f(x,y) funkcija f(x,y) jednoznačna i neprekinuta, dakle i omeđena, u nekom zatvorenom području ravnine (X,Y), a osim toga da je i izraz
f(x, y2) − f (x, y1)/y2−y1
omeđen u svake dvije točke (x,y1) i (x,y2) područja istih apscisa (što je na pr. ispunjeno, ako je parcijalna derivacija δf/δy neprekinuta u tom području). Uz te uvjete može se dokazati, da ima uvijek jedna i samo jedna integralna krivulja zadane jednadžbe, koja prolazi točkom (x0,y0) po volji izabranom u zadanom području, a neprekinuta je i ima tangentu, kojoj se položaj neprekinuto mijenja. U tu se svrhu izračuna naime, počevši od propisane vrijednosti y0, najprije funkcija y1(x) = y0 + ʃxx0f(x,y0)dx, s pomoću nje
y2=y0+ ʃxx0 f[x,y1(x)]dx i t. d., yn = y0+ ʃxx0 f(x,yn-1(x))dx
i načini beskonačan red
[y1(x)—y0] + [y2(x)—y1(x)] + ∙∙∙ + [yn(x)—yn-x(x)] + ∙∙∙, za koji se pokazuje, da za vrijednosti x iz nekoga intervala oko x0, koji se pobliže i određuje, taj red konvergira spram jedne funkcije y(x), koja je neprekinuta i ima neprekinutu derivaciju, a zadovoljava i diferencijalnu jednadžbu (Picardova metoda sukcesivnih aproksimacija). Iz dokaza izlazi, da je opće rješenje jednadžbe 1. reda dano izrazom
y(x) = y(x,C) ili F(x,y,C) = 0,
gdje je C konstanta po volji, koja se uvijek javljala i u svim dosadanjim slučajevima. Ako opći integral predočimo u geometrijskom obliku, dobivamo sustav krivulja u ravnini (integralne krivulje), koji zavisi o jednoj konstanti C, t. zv. parametru, koji može primiti vrijednosti po volji. Integralne krivulje, koje dobivamo, ako se za C uvrste posebne vrijednosti, jesu partikularna ili posebna rješenja jednadžbe, tako da se opće rješenje javlja kao skup svih partikularnih rješenja. Da se odredi jedno partikularno rješenje, treba odrediti onu vrijednost konstante C, koja tome rješenju pripada, a ta se odredi s pomoću t. zv. početnog uvjeta, koji se za jednadžbu 1. reda sastoji u tome, da se zada točka T0(x0,y0), kojom taj integral mora prolaziti. Uvrštenjem, naime, u izraz za opći integral koordinata točke T0 dobiva se jednadžba y0=y(x0,C), iz koje se odredi C; dalji tok integralne krivulje određen je jednoznačno diferencijalnom jednadžbom. Ali veza između skupa krivulja i jednadžbe 1. reda može se obrnuti. Svaki sustav krivulja u ravnini, koji zavisi o jednom parametru, zadovoljava jednu diferencijalnu jednadžbu 1. reda. Iz jednadžbe sustava F(x,y,C)=0 izlazi naime diferenciranjem po x, pazeći pri tome na to, da je u toj jednadžbi y funkcija od x,
δF/δx + δF/δy · y' = 0.
Ako se eliminira C iz te dvije jednadžbe, dobiva se izraz nezavisan od C, dakle nezavisan o pojedinim krivuljama sustava,
f(x,y,y') = 0
koji izriče stoga neko zajedničko svojstvo tangenata svih krivulja sustava i predočuje diferencijalnu jednadžbu 1. reda, kojoj je F(x,y,C) = 0 opći integral. Ako treba na pr. naći diferencijalnu jednadžbu sustava parabola y2 = 2Cx,
diferencira se ta jednadžba, što daje 2yy' = 2C; uvrstivši izraz za 2C u prvu jednadžbu, dobiva se diferencijalna jednadžba sustava y' = 1/2 y/x.
No sve to vrijedi samo u onom dijelu ravnine, u kome su ispunjeni uvjeti, pod kojima se dokazuje eksistencija jednoznačno određenoga rješenja; točke, u kojima uvjeti ne vrijede, zovu se singularne točke diferencijalne jednadžbe. Tim točkama može prolaziti i više integralnih krivulja, pače i beskonačno mnogo njih, ali i nijedna. Takva je singularna točka ishodište x=y=0 u jednadžbi y'= y/x, jer njome prolaze sve integralne krivulje y = Cx, koje su pravci kroz ishodište. I ovdje je H. Poincaré u stariju formalnu teoriju diferencijalnih jednadžbi unio nov život pokazavši, kako je proučavanje singularnih točaka od osnovnoga značenja za pregled integralnih krivulja sustava u cijelosti i kako upravo one određuju karakteristično vladanje tih krivulja pa dopuštaju i vrstanje njihovo u sasvim određene kategorije. Od njega potječe pojam i naziv kvalitativne integracije diferencijalnih jednadžbi za proučavanje tôka integralnih krivulja u njihovoj cijelosti, za razliku od kvantitativne integracije, kojom se dobivaju analitički izrazi i numeričke vrijednosti rješenja u dijelovima ravnine, u kojima nema singularnih točaka. Najjednostavnije singularne točke jesu: 1. čvorišta, u kojima se križa beskonačno mnogo integralnih krivulja (točka x = y = 0 jednadžbe y' = x/x); 2. rastjecišta, u kojima se sijeku dvije krivulje i samo dvije; 3. žarišta, oko kojih se krivulje ovijaju sve tješnje i u ovijanju se sve više asimptotički približuju tim točkama; 4. središta, koja okružuju zatvorene krivulje sužujući se sve većma prema tim točkama. Sastavljanjem takvih singularnih točaka nastaju zamršeniji singulariteti.
6. Diferencijalne jednadžbe višega reda. Diferencijalna jednadžba n-toga reda je oblika
F(x,y,y',y",..., y(n)) = 0 ili y(n) = f(x,y,y',..., y(n-1)). Rijetki su slučajevi, kada se već i diferencijalna jednadžba 2. reda (n=2) može integrirati elementarno; nastoji se, dakle, bar, da se nađu oni slučajevi, u kojima se red jednadžbe može sniziti.
a) Ako diferencijalna jednadžba 2. reda ne sadržava traženu funkciju y, ona je oblika
F(x,y',y") = 0.
Tada se uvodi derivacija y' kao nova tražena funkcija u; a jer je tada y" = du/dx, glasi jednadžba F(x,u,u') = 0, a to je jednadžba 1. reda.
b) Diferencijalna jednadžba ne sadržava x, t. j.
F(y,y',y") = 0.
Tada se y uzima kao nova nezavisna promjenljiva, y' kao nova funkcija, a y" = dy'/dx = dy'/y · y', pa jednadžba prima oblik diferencijalne jednadžbe 1. reda
F (y, y', dy'/dy · y') = 0.
Primjer za slučaj b) diferencijalna je jednadžba harmoničkog gibanja ili čistoga titranja
y" + n2 y = 0,
koja prelazi u jednadžbu 1. reda
dy'/dyy' + n2=y = 0,
u kojoj su promjenljive y' i y odijeljene. Njenu ćemo integraciju izvršiti u 7. drugim putem.
Za diferencijalne jednadžbe n-toga reda postoje slični slučajevi snizivanja reda. Opće rješenje diferencijalne jednadžbe n-toga reda je oblika
y (x) = y (x, C1,..., Cn),
gdje su C1,..., Cn konstante po volji. Geometrijski predočuje ono sustav krivulja u ravnini, koji zavisi o n nezavisnih parametara C1,..., Cn. Da se odredi jedno partikularno rješenje, treba odrediti tih n konstanata time, da se zada početni uvjet
y0 = y (x0), y'0 = y' (x0),..., y0 (n-1) = y (n-1) (x0),
t. j. vrijednost funkcije y(x) i njenih derivacija do uključivo reda (n-l)-oga za neku po volji zadanu vrijednost
argumenta x = x0. Za diferencijalnu jednadžbu 2. reda treba, dakle, zadati uvjet: točku (x0, y0), kojom integralna krivulja mora prolaziti, i smjer tangente u toj točki. Diferencijalne jednadžbe 2. reda važne su u primjenama, jer se njima opisuje na pr. gibanje materijalne točke po pravcu pod utjecajem sile, koja u najopćenitijem slučaju može zavisiti o položaju točke, njenoj brzini i vremenu t; ako pravac, po kome se točka giba, odaberemo za os X pa ako s x(t) označimo položaj točke u čas t, tada znači x(t) brzinu, a ẍ(t) akceleraciju gibanja (Dif. rač.), pa po osnovnom zakonu mehanike vrijedi jednadžba
mẍ(t) = f (t, x, x),
gdje je m masa točke, a f sila, koja na nju djeluje. Početni je uvjet sada položaj x točke u neki čas t = t0 i početna brzina x0 = x(t0) u taj čas. Oni jednoznačno određuju jedno moguće gibanje te točke.
7. Linearne diferencijalne jednadžbe. Ako diferencijalna jednadžba nije najopćenitijega oblika svoga reda, nego u svojoj građi pokazuje neku pravilnost, može se o svojstvima njenih rješenja izreći i više. Jedan je takav važan slučaj linearna diferencijalna jednadžba, t. j. jednadžba oblika
(a) any(n) + an-1y(n-1) +... + a2y" + a1y' + aoy = { f(x) 0,
gdje su koeficijenti an, an-1,...,a0, kao i f(x), zadane funkcije od x. Ako je f(x) ≠ 0, jednadžba je nehomogena, ako je f(x) = 0, jednadžba je homogena. Za homogene jednadžbe izlaze iz linearne građe njihove lijeve strane osnovno svojstvo, t. j. ako y1,..., yn predočuje n rješenja njenih, tada je i C1y1 + ∙∙∙ + Cnyn njeno rješenje, bile veličine C1,..., Cn kakvegod konstante. Na temelju toga svojstva pokazuje se također, da se opće rješenje linearne homogene diferencijalne jednadžbe može predočiti kao linearna kombinacija s konstantnim koeficijentima od n partikularnih rješenja, ako su ta partikularna rješenja linearno nezavisna, t. j. ako među njima nema nikakve veze oblika c1y1(x) + ∙∙∙ + cnyn(x) = 0, osim u slučaju, da su sve konstante c jednake nuli. Opće rješenje linearne homogene jednadžbe dano je dakle izrazom
y(x) = C1y1(x) + ∙∙∙ + Cnyn(x),
gdje su C1,..., Cn kakvegod konstante. Dalje se pokazuje, da se na temelju općega rješenja homogene jednadžbe može naći i opće rješenje nehomogene jednadžbe; ako je naime η(x) jedno partikularno rješenje nehomogene jednadžbe, a y(x) gornje opće rješenje homogene jednadžbe, koja joj pripada, tada je opće rješenje nehomogene jednadžbe oblika
η(x) + y(x) = η(x) + C1y1(x) + ∙∙∙ Cnyn(x).
Ako su koeficijenti ai (i=l,∙∙∙ n) konstante, linearna diferencijalna jednadžba može se integrirati elementarno. Jer uzme li se, da je rješenje homogene jednadžbe funkcija oblika y=ecx i dalje y'—cecx, y"=c2ecx,..., y(n) = cnecx, gdje je c još neodređena konstanta, prima diferencijalna jednadžba oblik
ecx (ancn + ∙∙∙ + a2c2 + a1 c + a0)=0,
a kako je uvijek ecx ≠ 0, mora konstanta c zadovoljavati t. zv. karakterističnu jednadžbu
Pn(c) = ancn + ∙∙∙ + a1c + a0 = 0.
Ako su c1,..., cn korijeni te jednadžbe i ako su svi među sobom različiti, opće je rješenje linearne homogene diferencijalne jednadžbe
y (x)=C1 ec1x + ∙∙∙ + Cn ecnx,
Ako je jedan korijen dvostruk, na pr. c1 = c2, partikularni integrali, koji mu pripadaju, jesu ec1x i xec1x; ako je p-struk, oni su ec1x, xec1x,..., xp-1ec1x.
Primjeri. 1. Točka mase 1 neka se giba na osi X pod utjecajem sile — n2x, razmjerne s apscisom x; ako je t vrijeme, ẍ akceleracija, glasi jednadžba gibanja
ẍ + n2x = 0;
ovdje je P2(c)=c2+n2, kojoj su korijeni c=±in, a opće rješenje
x(t) = Cx eint + C2 e—int.
Drugi je oblik rješenja
x(t)=A sinnt+B cosnt,
kako se može ovjeroviti uvrštavanjem u jednadžbu; A i B konstante su po volji. Ako se stavi još A = Ccosn, B = Csinn, može se istom rješenju dati i ovaj oblik
x (t) = C sin (nt + m),
gdje je C= + √ A2 + B2 , tg m = B/A. Gibanje je, dakle, periodičko perioda P = 2 π/n te se zove i čisto ili jednostavno titranje ili harmoničko gibanje.
2. Važna je u primjenama i jednadžba prigušenoga titranja
ẍ + a1 x + n2 x = 0,
koja opisuje gibanje točke na osi X, na koju djeluje osim sile —n2x i trenje —a1x razmjerno s brzinom. Narav gibanja zavisi o izrazu D = a12 — 4n2. Ako je D<0, rješenje je oblika
x (t) = C . e-a1/2 t sin √ n2 − a12/4 t
i predočuje slabo prigušeno gibanje; amplituda se titranja pri tome umanjuje s vremenom. Ako je D>0, x(t) = C1ec1t + C2ec2t, gdje je c1,2= — a1/2 ± √ a12/2 − n2 .
Prigušenje je sada jako, a gibanje je aperiodičko.
3. Diferencijalna jednadžba prisiljenoga titranja je oblika
x+a1x+n2x=f (t).
U tom slučaju djeluje na točku osim sila kao u 2. još i jedna vanjska sila f(t). Uzmimo, da je ta sila periodička, na pr. f(t) = Asinωt perioda P = 2 π/ω. Tada ima jedno partikularno rješenje jednadžbe, koje ima period P izvanje
sile: x(t) = Csin (ωt+φ). Gibanje, predočeno tim partikularnim rješenjem, zove se prisiljeno, jer mu je izvanja sila nametnula svoj period. Ako je koeficijent trenja a1 malen, a period izvanje sile P jednak periodu 2 π/n, što bi ga sustav, koji titra, imao, da nema trenja (a1 = 0) ni izvanje sile, nastaje slučaj rezonancije, u kome se titraji vrše s vrlo velikim amplitudama.
8. Sustavi diferencijalnih jednadžbi. Ako treba odrediti dvije funkcije od x,y(x) i z(x), koje su tako među sobom vezane, da zadovoljavaju dvije diferencijalne jednadžbe oblika
dy/dx = f1 (x, y z), (a)
dz/dx = f2 (x, y, z),
gdje su f1 i f2 zadane funkcije od x, y, z, kaže se, da te jednadžbe čine sustav od dvije obične diferencijalne jednadžbe 1. reda. Rješavanje takva sustava može se svesti na rješavanje obične diferencijalne jednadžbe 2. reda. Ako, naime, prvu jednadžbu diferenciramo po x, dobivamo
y'' = δ f1/δ x + δ f1/δ y dy1/dx + δ f1/δ z dz1/dx
pa ako iz te jednadžbe i dviju zadanih eliminiramo funkcije z i dz/dx, ostaje diferencijalna jednadžba 2. reda za funkciju y(x)
F(x, y, y', y") = 0.
Ako njeno opće rješenje y = y(x, C1, C2) uvrstimo u prvu jednadžbu (a), sadržava ona još samo funkciju z i argumenat x, odakle se može z odrediti, tako da dobivamo z = z (x, C1, C2).
Obrnuto, svaka obična diferencijalna jednadžba 2. reda može se pisati kao sustav od dvije diferencijalne jednadžbe 1. reda, ako se uvede prva derivacija kao pomoćna funkcija. Na pr. jednadžba ẍ + n2x = 0 može se pisati u obliku sustava
dx/dt = x1
dx1/dt = − n2x.
Slično vrijedi i za odnos između sustava od n diferencijalnih jednadžbi 1. reda i obične diferencijalne jednadžbe n-toga reda.
9. Parcijalne diferencijalne jednadžbe, a) Ako je z=z(x,y) funkcija dviju promjenljivih x i y, jednadžba
F (x, y, z δz/δx, δz/dy) = 0
zove se parcijalna diferencijalna jednadžba 1. reda. Budući da tražena funkcija z(x,y) predočuje u prostornom pravokutnom koordinatnom sustavu neku površinu, riješiti tu jednadžbu znači naći sve površine, kojih aplikate z kao funkcije od x i y identički zadovoljavaju tu jednadžbu. Rješenja su te jednadžbe, dakle, integralne površine. Nova okolnost pri rješavanju takvih jednadžbi jest, da u opće rješenje ne ulaze konstante po volji, nego funkcije po volji. To se vidi već u najjednostavnijem slučaju jednadžbe
δz/δx = f (x,y),
gdje je f(x,y) zadana funkcija od x i y. Najopćenitiji oblik funkcije, koja zadovoljava tu jednadžbu, jest
z(x,y) = ʃxx0 f(x,y) dx + f1(y),
gdje je f1(y) kakvagod funkcija argumenta y. Ako naime taj izraz diferenciramo po x, dobivamo upravo zadanu jednadžbu, jer je δf1 (y)/δx = 0, budući da je sada i y argumenat. Budući da je za x=x0 integral jednak nuli, to je z(x0,y)=f1(y), a funkcija po volji f1(y) predočuje, dakle, geometrijski presjek površine z(x,y) ravninom okomitom na os X u točki x = x0; svaka površina, koja prolazi kojomgod krivuljom u ravnini toga presjeka, integralna je površina.
Jednadžba
a δz/δx + bδz/δy = c
definira sve valjke u prostoru, kojima su izvodnice usporedne s pravcem određenim konstantnim koeficijentima a, b, c. Opće je rješenje, dakle, skup svih tih valjaka; da se nađe jedno partikularno rješenje, t. j. da se između svih valjaka odabere jedan posebni, treba zadati ravnalicu toga valjka, t. j. krivulju u prostoru, duž koje izvodnica toga valjka klizi, da taj valjak izvede. Izbor po volji ravnalice, kojom mora prolaziti valjak, unosi u taj problem onu neodređenost, koja je analitički izražena jednom funkcijom po volji.
b) Parcijalne diferencijalne jednadžbe 2. reda imaju u višoj analizi i matematičkoj fizici važno mjesto. Evo nekoliko primjera.
1. Diferencijalna jednadžba titranja žice
δ2y/δt2 = a2 δ2y/δx2,
gdje je a zadana konstanta, opisuje titranje homogene žice duljine d, upete u točkama x=0 i x=d osi X, koja je povučena iz položaja mirovanja na osi X i prepuštena svome gibanju. Traži se rješenje y=y(x,t), t. j. ordinata krivulje, koje oblik žica prima u točki apscise x intervala od 0 do d i u čas t, ali koje zadovoljava još i ove uvjete: prvo granični uvjet, koji propisuje, da na granicama intervala, t. j. za x=0 i x=d, mora biti y=0, jer je žica u tim točkama upeta, dakle y(0, t)=y(d, t)=0 u svaki čas t, i drugo početni uvjet, koji zadaje u početni čas t—0 oblik žice, y(x,0) = f(x), i brzinu svake točke žice δ y (x,t)/δ t = g(x); f(x) i g(x) su, dakle, zadane funkcije. Obično se počinje integracija te jednadžbe tako, da se traži rješenje oblika y(x,t) = X(x) ∙ T(t), koje je produkt jedne funkcije od x i jedne funkcije od t. Time se raspada parcijalna diferencijalna jednadžba u dvije obične diferencijalne jednadžbe 2. reda s konstantnim koeficijentima, koje vode do partikularnog rješenja diferencijalne jednadžbe oblika
y1 (x, t) = sin nπx/d (an cos nπat/d + bn sin nπat/d),
koje predočuje titranje perioda 2d/na. Radi linearnoga oblika jednadžbe i svaka je linearna kombinacija s konstantnim koeficijentima ovakvih titraja također rješenje, pa je napokon rješenje i funkcija predočena beskonačnim redom 
Koeficijenti an, bn u tom izrazu moraju se odrediti iz početnog uvjeta 
formulama poznatim iz teorije Fourierovih redova (v.). U drugu ruku, lako se možemo uvjeriti, da je opće rješenje te jednadžbe dano izrazom
y(x,t) = f1(x+at) + f2( x—at),
gdje su f1 i f2 dvije funkcije po volji, što odgovara redu n=2 te diferencijalne jednadžbe. Pri tome znači f1(x+at) krivulju, koja nastaje iz krivulje f1(x) usporednim pomicanjem duž negativne osi X, a f2(x—at) krivulju, koja nastaje isto takvim pomicanjem krivulje f2(x) duž pozitivne osi X. Funkcije f1 i f2 moraju se tako odrediti, da zadovoljavaju početni uvjet.
2. Diferencijalna jednadžba širenja topline u štapu
δT/δt = a2 δ2T/δx2; T je temperatura štapa duljine d, vrlo uskoga presjeka, koji leži na osi X, u točki apscise x i u čas t. Treba odrediti rješenje T(t,x), koje zadovoljava granični uvjet T(t,0)=0, T(t,d)=T 1, koji, dakle, znači, da na početku štapa vlada temperatura 0, na kraju temperatura T1, i početni uvjet T(0,x) = f(x), koji izriče, da je u početni čas t=0 zadana temperatura štapa u svakoj točki x zadanom funkcijom f(x). Teorija te jednadžbe pokazuje, da je jedan oblik rješenja 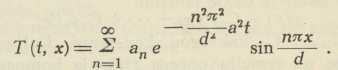
Koeficijente an treba odrediti tako, da to rješenje zadovoljava početni uvjet 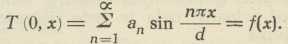
3. Laplaceova diferencijalna jednadžba ili jednadžba potencijala
δ2V/δx2 + δ2V/δy2 = 0 u ravnini i δ2V/δx2 + δ2V/δy2 + δ2V/δz2 u prostoru, koju nalazimo u različnim dijelovima matematičke fizike. Prvu zadovoljava realni i imaginarni dio svake analitičke funkcije (→ Funkcija). Opće je rješenje njeno oblika
V(x,y) = f1(x + iy) + f2(x — iy),
gdje su i f1 i f2 funkcije po volji kompleksnih argumenata x + iy i x — iy, koje moraju biti konjugirano kompleksne, ako funkcija V(x,y) mora biti realna. Te se jednadžbe zovu i diferencijalne jednadžbe potencijala, jer ih zadovoljavaju potencijali (v.). Za te jednadžbe osnovan je problem Dirichletov, koji se sastoji u tome, da se odredi rješenje, neprekinuto s neprekinutim prvim i drugim derivacijama, koje duž zadane zatvorene krivulje u ravnini ili na zadanoj zatvorenoj površini u prostoru prima zadane vrijednosti.
LIT.: Sva veća djela o diferencijalnom i integralnom računu, navedena u članku Diferencijalni račun, sadržavaju i teoriju diferencijalnih jednadžbi. K tome pridolazi L. Bieberbach, Theorie der Differentialgleichungen, 3. izd., Berlin 1930, J. Springer; W. Hort, Die Differentialgleichungen des Ingenieurs, 2. izd., Berlin 1925, J. Springer; E. Kamke, Differentialgleichungen reeller Funktionen, Leipzig 1930, Isti, Differentialgleichungen. Lösungsmethoden u. Lösungen. I. Gewöhnliche Differentialgleichungen, 2. izd., Leipzig 1943. Vrlo zgodna mala djela su G. Hoheisel, Gewöhnliche Differentialgleichungen i L. Hopf, Einführung in die Differentialgleichungen der Physik (Sammlung Göschen, br.920, dotično 1070). Opširna su djela E. L. Ince, Ordinary differential equations, London 1926.Ž. M.