DIFERENCIJALNI RAČUN. Problemi i metode, koji čine predmet diferencijalnoga računa, javili su se u drugoj polovini 17. st., pošto je obnavljanje algebre po F. de Vièteu i uvođenje novih analitičkih metoda u geometriju (→ analitička geometrija) po P. de Fermatu i R. Descartesu utrlo put za razvoj novih istraživanja, koja su bila od osnovnoga značenja za svu matematičku nauku kao i za njene primjene. Dva su problema na ulazu u diferencijalni račun, na kojima su se razvili osnovni pojmovi i postupci njegovi. Jedno je geometrijski problem određivanja tangente na zadanu krivulju i određivanje točaka, u kojima ordinate krivulje imaju najveću ili najmanju vrijednost; drugo je promatranje toka prirodnih pojava, a napose brzine, kojom se neprekinuti neki pojav mijenja s vremenom, ili, općenitije, u ovisnosti o drugoj kojoj promjenljivoj veličini.
Problem tangente. Stari grčki matematici znali su konstruirati tangente na neke krivulje (kružnicu, čunosječnice, Arhimedovu spiralu), no uvođenjem analitičke geometrije nastao je problem, da se nađe opća analitička metoda za konstrukciju tangente na bilo koju krivulju, zadanu jednadžbom u pravokutnom koordinatnom sustavu. S različnih strana, u malom razmaku vremena, bez međusobnog utjecaja, nikli su u drugoj polovini 17. st. postupci za rješenje toga problema, koji se u današnjem obliku mogu predočiti ovako.
 Sl. 1.
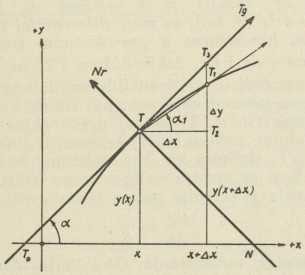
Sl. 1.Neka je zadana u pravokutnom koordinatnom sustavu krivulja, koje jednadžba glasi y = y(x); ona neka je neprekinuta funkcija (v.) od x u intervalu a x b, što znači, da se kojegod dvije njene ordinate y iz toga intervala razlikuju po volji malo, ako su njihove apscise x dovoljno blizu. Da definiramo tangentu na tu krivulju u točki T(x,y) (slika 1), pomaknimo se na osi apscisa od točke x do točke x + Δx; znakom Δx, koji se čita »prirast x-a«, označili smo razmak tih dviju točaka na osi X. Taj prirast može biti pozitivan ili negativan, prema tome, da li smo se pomakli desno od x ili lijevo. Radi promjene vrijednosti apscise x, promijenila se i vrijednost funkcije: od vrijednosti y(x) u točki x prešla je na novu vrijednost y(x+Δx) u točki x+Δx, koja je jednaka prijašnjoj vrijednosti funkcije, uvećanoj ili umanjenoj za neki »prirast y-a«, koji označujemo s Δy. Prirastu apscise Δx pripada, dakle, prirast vrijednosti funkcije Δy=y(x+Δx)—y(x). Neka je T1 točka na krivulji s koordinatama x+Δx, y+Δy. Spojimo točke T i T1 pravcem, koji se zove sekanta. Neka taj pravac zatvara s pozitivnim smislom osi X kut a1; smjer toga pravca mjerit ćemo veličinom tgα1 = Δy/Δx, koja se zove uspon sekante u T. Pustimo sada, da se točka T1 neprestano približuje po krivulji točki T tako, da joj može doći i po volji blizu, a da nikada ne stigne u točku T, t. j. uzmimo, da točka teži točki T kao granici (v.). Pri tome će se i prirast Δx neprestano umanjivati i moći će postati po volji malen, a radi neprekinutosti funkcije y(x) vladat će se isto tako i prirast funkcije Δy; kako se kaže u matematici, i Δx i Δy težit će nuli. Sekanta TT1, koja prolazi uvijek čvrstom točkom T, mijenjat će pri tome svoj smjer, pa će se i kut α1 mijenjati, ali u svakom položaju točke T1 taj će smjer biti određen veličinom tgα1 prema gornjoj jednadžbi. Tada će se redovito dogoditi, da će se ta pomična sekanta sve većma približavati svojim smjerom smjeru čvrstoga jednoga pravca, tako da će smjer sekante težiti smjeru toga pravca. Taj će smjer biti određen nekim kutom α, kojemu teže kutovi sekanata α1, kada T1 teži točki T kao granici. Taj čvrsti pravac u točki T, određen veličinom tgα, zove se tangenta krivulje u točki T(x,y). Ako se poslužimo oznakom lim (od lat. limes »granica«) za označivanje granice, kojoj teži promjenljiva neka veličina, i ako označimo s Δx→0 ono neprestano umanjivanje prirasta apscise x i teženje nuli, bit će smjer tangente na zadanu krivulju u točki T ili uspon tangente određen jednadžbom:
tgα = lim Δy/Δx = lim y (x + Δx) − y(x)/Δx, kad Δx →0.
Derivacija. Omjer Δy/Δx, koji je određivao smjer sekante TT1, zove se i kvocijent diferencija; a granica, kojoj on teži, kada točka T1 teži točki T, zove se derivacija funkcije y(x) u točki (x,y). Mjesto derivacija kaže se i diferencijalni kvocijent, iz razloga, koji će se vidjeti poslije. Derivacija se označuje s Dxy ili s y'(x) i čita »derivacija funkcije y(x) po x«. Definicija derivacije jest dakle:
Dxy = y'(x) = lim Δy/Δx, kad Δx→ 0.
Određivanje derivacija funkcija i primjena njihova na izučavanje svojstava funkcija predmet je diferencijalnoga računa. Derivacija je osnovni pojam d-a r-a. Izračunati derivaciju zadane funkcije kaže se i derivirati ili diferencirati funkciju. Budući da je Dxy = tgα, određuje vrijednost derivacije veličinu tgα, dakle i kut α, što ga zatvara tangenta na krivulju y(x) u točki (x,y) s pozitivnim smislom osi X. Time je u teoriji riješen problem tangente.
Primjer. Neka je zadana funkcija y(x) = x2, koja predočuje parabolu s vrhom u ishodištu koordinatnoga sustava, a simetričnu s obzirom na os Y. Da izračunamo njenu derivaciju u zadanoj točki apscise x, načinimo izraz za prirast te funkcije Δy = (x+Δ)2—x2=2x. Δx + (Δx)2; prema tome je kvocijent diferencija Δy/Δx = 2x + Δx; kada Δx→0, desna strana teži izrazu 2x, dakle je Dxx2 = 2x. Na pr. u točki x = 1/2, y= (1/2)2 = 1/4 vrijednost derivacije je 1, t. j. tgα = l; tangenta na parabolu u toj točki čini dakle kut od 45º s pozitivnim smislom osi X. Uspon tangente u točki T daje i smjer krivulje u točki T, tako da poznavanje derivacije olakšava znatno i konstrukciju krivulje.
Formule diferenciranja. Za računanje s derivacijama izvode se opće formule i posebne za pojedine vrste važnijih funkcija.
a) Opće formule. Za derivaciju zbroja ili razlike dviju funkcija u(x) i v(x) vrijedi:
(u ± v)' = u' ± v'.
Za produkt: (u ∙ v)' = u'v + uv'.
(c ∙ u)' = cu', gdje je c konstanta.
Za kvocijent:
(u/v)' = vu' − uv'/v2
Ako je y(x)=y[u(x)] t. zv. složena funkcija od x, tako da y zavisi od x ne neposredno, nego preko funkcije u(x) (na pr. y=sin2x, gdje je y=u2, a u=sin x), vrijedi formula: y'(x) = y'(u) ∙ u'(x).
b) Posebne formule za neke funkcije.
| Funkcija |
Derivacija |
| y = c, c konstantno |
y’=0 |
| =xn |
=nxn-1 |
| =sinx |
=cosx |
| =cosx |
=—sinx |
| = lnx |
1/x |
| = ex |
= ex |
| = arcsinx |
1/√ 1−x2 |
| = arctgx |
1/1+x2 |
| = arshx |
1/√ 1+x2 |
| = arthx |
1/1−x2 |
Geometrijska primjena. Tangenta na krivulju u točki T(x,y) je pravac, koji prolazi tom točkom (diralištem), a uspon mu je dan vrijednošću derivacije u toj točki; dakle je jednadžba tangente:
Y—y=y'(x) ∙ (X—x),
gdje su x,y koordinate zadanoga dirališta, a X,Y koordinate kojegod točke toga pravca. Pravac, okomit na tangentu u točki T, zove se normala krivulje u točki T; jednadžba joj je:
Y−y = – 1/y'(x) (X−x)
budući da su okomiti pravci u analitičkoj geometriji označeni time, da imaju uspone recipročne i protivnoga predznaka.
Tangenta Tg i normala Nr krivulje određuju u koordinatnom sustavu neke dužine, koje su važne u diskusiji krivulja. Dužina T0x, određena sjecištem T0 tangente s osi X i podnožištem x točke T, zove se subtangenta St krivulje; iz slike 1. izlazi, da je St=y ∙ ctgα = y/y'. Subnormala Sn je dužina xN; dakle je Sn=y ∙ tgα=yy'. Daljina dirališta T od sjecišta T0 je duljina tangente, a daljina dirališta T od N je duljina normale. G. W. Leibniz, uz I. Newtona, jedan od osnivača diferencijalnog računa, pošao je prvotno (1673) od geometrijskoga problema određivanja subtangente.
Brzina gibanja. Za Newtona, koji se u Engleskoj već oko g. 1666 počeo baviti problemima diferencijalnoga i integralnog računa, bio je osnovni pojam d-a r-a brzina gibanja ili uopće brzina promjene veličina, koje se mijenjaju s vremenom kao predstavnikom nezavisne promjenljive uopće. Za nezavisnu promjenljivu uzima Newton, da se mijenja jednolično brzinom 1, a promatra brzine, kojima se uvećavaju ili umanjuju zavisne promjenljive (funkcije), koje on zove fluentima (lat. fluens »tekući«). I za geometrijske veličine uzima Newton, da nastaju gibanjem (na pr. crta gibanjem točke) tako, da se u svima tim problemima javlja prirodno misao o brzini. Brzinu promjene nekoga fluenta naziva on fluksija; ona nije drugo nego derivacija fluenta po nezavisnoj promjenljivoj. Fluksiju veličine y označuje Newton s ẏ (1671). Osnovni problem d-a r-a glasi u Newtona: ako je zadan put, koji prolazi neka točka, kao funkcija vremena, naći fluksiju toga gibanja; stoga i zove Newton svoju metodu kasnije i račun fluksija. Ako je gibanje jednolično, put, što ga točka prođe u vremenu t, dan je izrazom s = c ∙ t, gdje je c konstanta. Brzina jednoličnoga gibanja je kvocijent diferencija Δs/Δt = c te je konstantna. Ako gibanje nije jednolično, nego je put predočen nekom funkcijom s=s(t), kvocijent Δs/Δt nije više konstantan i ne predočuje brzinu gibanja u čas t, nego samo srednju brzinu toga gibanja u vremenskom intervalu Δt; brzina gibanja u času t definira se kao granica, kojoj teži ta srednja brzina, kad je promatramo u sve kraćim i kraćim razmacima Δt, kad, dakle, puštamo, da interval Δt teži nuli. Dakle je brzina v dana izrazom:
v=lim Δs/Δt, kad Δt → 0.
Iz toga vidimo, da je brzina određena formalno istim izrazom, kojim i derivacija. Primjer. Slobodni pad dan je jednadžbom s = gt2; brzina mu je v = g ∙ 2t = gt.
Diferencijal. Pod diferencijalom dy funkcije y(x) razumijeva se produkt derivacije funkcije i prirasta argumenta x: dy = y'(x) ∙ Δx. Jer je y'(x) = tgα, dakle dy = tgα ∙ Δx, znači diferencijal geometrijski prirast T2T3 (sl. 1) ordinate tangente na krivulju u točki T(x,y), koji nastaje radi pri
rasta apscise x za Δx. Diferencijal funkcije razlikuje se, dakle, od prirasta funkcije, no pokazuje se, da se njihova razlika može učiniti po volji malom, ako je Δx dovoljno malen prirast. Newton zove diferencijal funkcije momentom funkcije. Mjesto Δx može se pisati i dx, jer po gornjoj definiciji dx je jednak Δx (D?x=l), i to vrijedi samo za diferencijal nezavisne promjenljive x; stoga je konačni izraz za diferencijal: dy = y'(x)dx. Uvođenje diferencijala nije teoretska potreba d-a r-a; korist toga sasvim je formalna, ali ta je znatna. Derivacija, koja po svojoj definiciji nije kvocijent, može se upotrebom diferencijalâ pisati u obliku kvocijenta: y'(x) = dy/dx, što za računanje s derivacijama, pa kasnije u integralnom računu, ima velikih formalnih prednosti. Derivacija se stoga zove i diferencijalni kvocijent, a operiranje s derivacijama i diferenciranje. Sistematsko upotrebljavanje diferencijalne oznake i izradba jednostavnoga i preglednoga algoritma (v.) za taj račun bio je uzrok, da je u infinitezimalnom računu prevladala Leibnizova simbolika.
Svaka se formula za račun s derivacijama može pisati u obliku formule s diferencijalima. Na pr.
d(u ± v) = du ± dv
d(u ∙ v) = v ∙ du + udv
d u/v = vdu−udv/v2
dc = 0, c konst.
dxn =nxn-1 ∙ dx
dex =ex dx
d lnx = 1/x dx
d sinx =cosx ∙ dx, i t. d.
S dx i dy vezana je i veličina ds jednadžbom: dx2 + dy2 = ds2; ds, koji se zove diferencijal luka krivulje, znači, dakle, hipotenuzu u pravokutnom trokutu TT2T3, kome su katete dx i dy, dakle dužinu TT3 na tangenti. Taj je trokut znamenit u povijesti diferencijalnoga računa, jer je pri njegovu promatranju prvi put sinula Leibnizu misao novoga računa (1673). U svojoj prvoj objavljenoj radnji o diferencijalnom računu (1684) Leibniz, iz sličnosti trokuta TT2T3 i T0xT, definira dy kao veličinu, koja se odnosi prema dx, koji se smatra veličinom po volji, kao što se odnosi ordinata y krivulje prema subtangenti, dakle dy/dx = y/St.
Infinitezimalna razmatranja. Definicija derivacije kao granice kvocijenta diferencija potječe uglavnom iz novijeg vremena, koje je unijelo jasnoću i strogost u pojam graničnoga približavanja (A. L. Cauchy, v.). Prije toga dolazilo se do pojmova diferencijalnoga i integralnog računa t. zv. »infinitezimalnim razmatranjima«, t. j. postupcima, koji su uvodili »beskonačno male« ili »infinitezimalne« veličine. Danas se pod beskonačno malom veličinom razumijeva svaka promjenljiva veličina, koja teži nuli. Ali u vrijeme osnivanja diferencijalnoga računa taj je pojam bio još dosta neodređen i neupućene je mogao zavesti u bludnju. Tangenta na krivulju bio je pravac, koji spaja dvije »beskonačno blize« točke krivulje; dio tangente između tih točaka identificirao se s lukom krivulje između tih točaka; taj dio krivulje bio je »beskonačno malen« dio njen, a konačan luk njezin bio je neki višekut od »beskonačno mnogo beskonačno malih« stranica. Ipak u rukama spretnih onih osnivača infinitezimalnoga računa i njihovih sljedbenika izlazili su rezultati, koji su bili većinom ispravni, kao što se i danas mogu vršiti takva razmatranja, pače i s korišću, ako se radi s nužnim oprezom.
Više derivacije i diferencijali. Ako prva derivacija, koja je funkcija od x, ima i sama derivaciju, zove se ta derivacija druga derivacija funkcije y(x) i označuje s y'' (x) ili Dx2y. Na pr. y=xn, y"=n(n-l)xn-2; y=ex y"=ex. Ako postoji derivacija druge derivacije, zove se ona treća derivacija funkcije y(x) i bilježi s y‴(x) ili Dx3y; korak po korak dolazi se i do n-te derivacije y(n)(x) ili Dx ny. Za funkciju y=xn je y‴=n(n-1)(n-2)xn-3, y(n)=n(n-1)(n-2) ...2 ∙ l = n!.
Drugi diferencijal funkcije je produkt druge derivacije i kvadrata diferencijala argumenta x: d2y=y"(x)dx2; slično je dny = y(n)(x)dxn.
Akceleracija gibanja. Druga derivacija puta po vremenu, t. j. brzina, kojom se mijenja brzina gibanja, važna je u kinematici (v.); ona se zove akceleracija gibanja. Jednaka je i prvoj derivaciji brzine po vremenu. Ako je put s = s(t), akceleracija je a = s"(t) = v'(t). Na pr. za slobodan pad je s = 1/2 gt2, v = s'(t) = gt, a = s"(t) = g.
 Sl. 2.
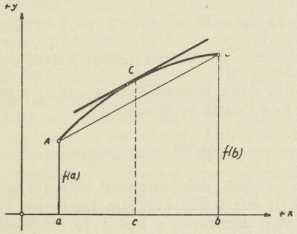
Sl. 2.Predznak derivacije. Ako je prva derivacija funkcije u nekoj točki pozitivna, t. j. kut α, što ga zatvara tangenta na krivulju u toj točki, šiljat, funkcija prolazi tom točkom rastući; ako je negativan, prolazi ona njome padajući. Ako je druga derivacija funkcije y(x) pozitivna za neki x = x0, dakle, ako je prva derivacija, t. j. uspon tangente tgα rastuća funkcija od x, krivulja je konkavna spram pozitivne osi Y, t. j. u okolišu točke x0,y0 leži iznad svoje tangente u toj točki. Ako je ta derivacija negativna, krivulja je konveksna prema osi Y, t. j. leži ispod svoje tangente u neposrednom okolišu te točke. Budući da je za parabolu y = x2 y" = 2, dakle druga derivacija uvijek pozitivna, ta je parabola u svakoj točki konkavna prema osi + Y.
Ako je y"(x) neprekinuta funkcija od x, ne može krivulja y = y(x) prijeći iz konkavnosti u konveksnost ili obrnuto, ako u prelaznoj točki nije y"=0. Apscise x0, koje zadovoljavaju tu jednadžbu, pripadaju točkama, u kojima krivulja može imati točku infleksije. Ako je za takav x0 y‴(x0) ≠ 0, krivulja ima sigurno točku infleksije; tangenta na krivulju u takvoj točki zove se tangenta infleksije. Ona krivulju i siječe i dira u točki x = x0, pa je krivulja s jedne strane točke infleksije iznad tangente, s druge ispod nje. Na pr. krivulja y=x3 ima točku infleksije u x0=0, jer je y"=6x = 0 za x0=0, a y‴(x0)=6.
Teorem srednje vrijednosti. Taj jednostavan i važan teorem ishodište je za dalju izgradnju d-a r-a, a sadržaj mu je ovaj (sl. 2). Ako spojimo dvije točke A i B krivulje y = f(x) tetivom AB, tada ima bar jedna točka na luku krivulje AB, u kojoj je tangenta usporedna s tetivom AB, ako krivulja ima određenu tangentu u svakoj točki toga luka; u formuli:
f(b)−f(a)/b−a = f'(c)
gdje je c neka vrijednost od x između a i b pobliže neodređena. Uza sve to dopušta nam ta formula često, da se ocijeni prirast f(b)—f(a) funkcije u intervalu od a do b, što je i od teoretske važnosti, a daje često i znatne numeričke rezultate. Ako je f(a)=f(b)=0, t. j. ako su a i b dvije nultočke funkcije f(x), izlazi da je f'(c)=0, t. j. između dvije nultočke funkcije f(x) leži bar jedna nultočka njene prve derivacije (Rolleov teorem).
S pomoću teorema srednje vrijednosti dokazuje se na pr., da je funkcija, kojoj je derivacija jednaka nuli u svakoj točki jednoga intervala, konstantna u tom intervalu, t. j. iz y'(x)≡0 slijedi y=C; i da se dvije funkcije, koje imaju iste derivacije, razlikuju samo za konstantu; na pr. funkcije y = x2 i y = x2+3, koje imaju istu derivaciju y' = 2x.
Taylorova formula. Ona je poopćenje teorema srednje vrijednosti. Ako funkcija f(x) ima u svim točkama nekog intervala određene, konačne derivacije do uključivo reda (n + l)-oga, tada je vrijednost funkcije u nekoj točki x0 + h
toga intervala predočena vrijednošću funkcije i njenih derivacija u točki x0 u obliku:
f(x0+h) = f(x0) + h/1!f'(x0) + h/2!f″(x0) +...+ hn/n! f(n) (x0) + hn+1/(n+1)! f(n+1)(c), gdje je c neka vrijednost između x0 i x0 + h, pobliže neodređena, ali koja nam uza sve to ne će smetati, upravo kao ni kod teorema srednje vrijednosti, da ocijenimo vrijednost funkcije, što je i od teoretske i numeričke važnosti. To je formula Taylorova (1717); posljednji član zove se ostatak, i to Lagrangeov. Ekvivalentni oblik toga teorema je i ovaj:
f (x) = f (x0) + x−x0/1! f' (x0) +...+ (x−x0)n/n! f(n)(x0) + (x−x0)n+1/(n+1)! f(n+1) (c), x0
Za n=0, x=b, x0=a izlazi teorem srednje vrijednosti u obliku: f(b) = f(a) + (b—a)f'(c). Ako je x0=0, gornja formula prelazi u Mac Laurinovu:
f(x)=f(0) + x/1! f'(0)+...+ xn/n! f(n) (0) + xn+1/(n+1)! f (n+1) (c), 0 < c < x.
Obje formule služe u prvom redu za približno određivanje ili aproksimaciju vrijednosti funkcija. Po toj je formuli vrijednost funkcije u točki x0+h izražena kao zbroj jednoga polinoma (v.) stepena n-toga i ostatka. Ako se može pokazati za neku funkciju, koja ima dovoljan broj viših derivacija, da je ostatak u njenoj Taylorovoj formuli vrlo malen, ako se samo pođe u formuli dosta daleko, t. j. ako se uzme dosta velik broj članova u polinomu, može se mjesto vrijednosti funkcije izračunati vrijednost polinoma, koja izlazi za zadani h, a koja se može elementarno odrediti. Ta aproksimacija zadane funkcije u nekom intervalu s polinomom osobito je važna u slučaju, da funkcija ima određene, konačne derivacije svakoga reda, kao na pr. funkcije ex, sin x, cos x, i da je takve naravi, da se ostatak može učiniti po volji malen, ako uzmemo u polinomu dovoljno velik broj članova; tada možemo aproksimirati vrijednost funkcije u zadanom intervalu po volji točno s polinomom dovoljno visoka stepena, pa točnosti aproksimacije teoretski nema granice. Taylorova formula prelazi time u beskonačan Taylorov red:
f(x) = f(x0) + x−x0/1! f'(x0) + ...+ (x−x0)n/n! f(n)(x0) + ..., koji konvergira (v.) u zadanom intervalu k vrijednosti funkcije f(x). Za x0=0 red se zove Mac Laurinov.
Tako se dolazi do redova za najvažnije funkcije u višoj analizi, s pomoću kojih se izračunavaju njihove vrijednosti numerički. Evo nekih:
ex = 1 + x/1! + x2/2! + ... + xn/n! + ...,
sinx = x — x3/3! + x5/5! − ... + (—1) n-1 x2n−1/(2n−1)! + ...,
cosx = 1 — x2/2! + x4/4! − ... + (—1)n-1 x2x2n-2/(2n-2)! + ...,
koji konvergiraju za svaku konačnu vrijednost od x. Iz prvoga reda izlazi i izraz za važnu konstantu e, osnovku prirodnih logaritama (v.),
e = 1 + 1/1! + 1 +... + 1/n!
Navedimo još i redove za funkcije:
ln(1 + x) = x— x2/2 + x3/3 − ... + (−1)n−1 xn/n + ...,
(1+x)m = 1 + (m/1x + m(m−1)/1·2 x2 + ...
m(m−1) ... [m(n−1)]/1·2 ... n
koji konvergiraju samo za vrijednosti x-a između —1 i +1.
Iz tih formula izlaze neke približne vrijednosti, koje se često upotrebljavaju u numeričkom računanju; na pr. sinx=x, koja vrijedi za male lukove x; iz posljednjeg, t. zv. Newtonova binomnoga reda, izlaze približne formule, važne za računanje s korijenima:
√ 1-x = 1 + 1/2 x; 3√ 1 + x = 1 + 1/3 x; 1/√ 1 + x = 1 - 1/2 x, gdje znak znači približno jednako.
Ekstremne vrijednosti. Važna primjena Taylorove formule jest određivanje ekstremnih vrijednosti funkcije, dakle njenih maksima i minima. Funkcija f(x) ima maksimum za x=x0, ako joj je vrijednost f(x0) u toj točki veća od svih njenih vrijednosti u neposrednom okolišu te točke, a minimum, ako joj je vrijednost manja od svih susjednih vrijednosti. Geometrijski je očevidno, a izlazi i iz Rolleova teorema, da je tangenta na krivulju u točki ekstrema horizontalna, t. j. f'(x0)=0, ako krivulja ima tangentu u toj točki. Već su i prije N. Oresme (14. st.) i J. Kepler (17. st.) primijetili tu činjenicu, da se funkcija u točki ekstrema najsporije mijenja. Uvjet f'=0 nuždan je za postojanje ekstrema, ali nije dovoljan. Na pr. y'=x3 ima u ishodištu x0=0 horizontalnu tangentu (y'=3x2,y'(0)=0), a ipak nema u toj točki ekstrem, nego točku infleksije. Dovoljan uvjet daje Taylorova formula za funkcije s dovoljnim brojem viših derivacija. Neka je x0 jedno rješenje jednadžbe f'(x)=0. Da funkcija za x=x0 ima ekstrem, dovoljno je, da prva od viših derivacija, koja se ne poništava za x=x0, bude tâkoga reda (parnoga), dakle 2., 4., 6.,... Ako se već druga derivacija ne poništava, t. j. ako je y"(x0)≠0, funkcija ima ekstrem, i to maksimum, ako je y"(x0)<0, minimum, ako je y"(x0)>0. Ako je to istom četvrta, kao u funkcije y=x4, opet ima funkcija ekstrem. Ali ako je y"(x0)=0, a y‴(x0)≠0, funkcija sigurno nema ekstrema, nego točku infleksije.
Neodređeni oblici. Pod određivanjem t. zv. neodređenih oblika razumijeva se izračunavanje granica nekih izraza, koji se neposredno javljaju u dva glavna oblika: 0/0 i ∞/∞; tako se izraz sin x/x za x0 =0 javlja u prvom, a log x/x za x → ∞ u drugom obliku. Općenito, ako je y(x) = f(x)/g(x), a f(x0) = g(x0)=0, y(x0) se javlja u prvom obliku; ako f(x) i g(x) teže u beskonačnost, kad x teži k x0, y(x) se javlja u drugom obliku. Vrijednost, koja će se pridati takvom neodređenom obliku, definira se kao granica (ako postoji), kojoj teži izraz f(x)/g(x), kad x teži k x0, t. j.
y(x0)=lim f(x)/g(x) za x → x0,
pri čemu x0 može biti konačan broj ili x može težiti i u beskonačnost. Ako funkcije f(x) i g(x) zadovoljavaju uvjete Taylorove formule, pokazuje se pomoću nje, u slučaju prvoga oblika, da je y(x0) = lim f(x)/g(x) = f'(x0)/g'(x0), da je dakle vrijednost neodređena oblika jednaka kvocijentu derivacije brojnika i derivacije nazivnika u točki x0. Ako se i prve derivacije poništavaju u x=x0, a možda i nekoliko viših derivacija, na pr. do uključivo reda (n—1)-oga, tada je
y(x0) = fn(x0)/gn(x0) (pravilo l'Hospitalovo).
Tako je 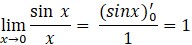 . Često je korisniji ovaj oblik:
. Često je korisniji ovaj oblik:
y(x0) = lim f(x)/g(x) = lim f'(x)/g'(x) za x → x0.
Obim se oblicima toga pravila određuje i vrijednost drugoga neodređena oblika ∞/∞. Na pr. za x → ∞
lim lnx/x = lim (lnx)'/1 = lim 1/x = 0.
Zakrivljenost. Osim konstrukcije tangente i normale na krivulju, pa upotrebe pojma derivacije u diskusiji toka krivulje, kako je već spomenuto, vodi metoda diferencijalnoga računa i do pojma zakrivljenosti krivulje. Kružnica je krivulja svagdje jednake zakrivljenosti, koja se po dogovoru mjeri izrazom 1/r, gdje je r polumjer kružnice. Isti se izraz za zakrivljenost kružnice dobije, ako se kut dviju tangenata kružnice razdijeli duljinom luka, koji spaja njihova dirališta. Kod svake druge krivulje zakrivljenost se mijenja od točke do točke; kut Δα, što ga tvore tangente na krivulju u točkama T i T1 (sl. 1), razdijeljen duljinom luka TT = Δs, daje sada samo »srednju zakrivljenost« Δα/Δs krivulje duž luka Δs. Zakrivljenost u točki T bit će granica ako postoji), kojoj teži srednja zakrivljenost Δα/Δs kada T1 teži po krivulji točki T kao granici. I ona se označuje s 1/R; imamo dakle za Δs → 0
1/R = lim Δα/Δs = dα/ds = zakrivljenost krivulje u točki T.
Ako je krivulja dana jednadžbom y=y(x), njena zakrivljenost u točki (x,y) dana je izrazom:
1/R = y''/(1 + y'2)3/2
Da se zorno predoči zakrivljenost krivulje u nekoj točki, konstruira se u toj točki krivulje kružnica, koja ima istu tangentu, koju i krivulja, a kojoj je središte na normali krivulje u toj točki u daljini R od točke. Ta kružnica, koja svojom zakrivljenošću predočuje zakrivljenost zadane krivulje u onoj točki, zove se kružnica zakrivljenosti u točki (x,y), njen polumjer polumjer zakrivljenosti krivulje u toj točki, a središte njeno središte zakrivljenosti u istoj točki. U točki infleksije (y"=0) zakrivljenost krivulje jednaka je nuli.
Kad se točka T pomiče po krivulji, a pri tom se tangenta mijenja neprekinuto i ne dolazi na tom dijelu krivulje točka infleksije, opisuje središte zakrivljenosti krivulju, koja se zove evoluta zadane krivulje; krivulja, od koje smo pošli, zove se u tom odnosu evolventa.
Djelomične derivacije. Kad je zadana funkcija od dvije ili više promjenljivih veličina, na pr. z=z(x,y) ili w= w(x,y,z), može ona imati derivacije, ako je smatramo kao funkciju samo od jedne od tih promjenljivih, a druge pri tome ne mijenjamo. U slučaju funkcije dviju promjenljivih z=z(x,y), promatrat ćemo dakle najprije z kao funkciju od samoga x, a y ćemo držati nepromijenjen i tražit ćemo derivaciju te funkcije po x; isto ćemo tako promatrati iza toga z kao funkciju od samoga y, a držat ćemo čvrst x i izračunati derivaciju. Tako se dolazi do djelomičnih (parcijalnih) derivacija prvoga reda te funkcije, koje se označuju ili s zx,zy, ili s ∂z/∂x, ∂z/∂y. Na pr. za z=x2+y2 imamo zx = 2x, zy = 2y.
Izraz dz = ∂z/∂x dx + ∂z/∂y dy zove se potpuni diferencijal funkcije z(x,y). Kako je prva derivacija funkcije jedne promjenljive bila u vezi s tangentom na krivulju u točki (x,y), tako su i djelomične derivacije funkcije dviju promjenljivih u vezi s tangentnom ravninom površine, koja je predočena u prostornom koordinatnom sustavu (X,Y,Z) jednadžbom z=z(x,y). Jednadžba te ravnine glasi:
Z — z = ∂z/∂x (X—x) + ∂z/∂y (Y—y);
ona dira površinu u točki (x,y,z), pa se dovoljno mali dio te ravnine u okolišu dirališta razlikuje od dijela površine u susjedstvu dirališta po volji malo, ako je to susjedstvo dovoljno blizo.
Svaki izraz oblika:
P(x,y)dx+Q(x,y)dy
nije uvijek potpuni diferencijal jedne funkcije dviju promjenljivih. Nuždan i dovoljan uvjet za to jest, da funkcije P(x,y) i Q(x,y) u području, u kome su definirane, identički zadovoljavaju uvjet: ∂P/∂y = ∂Q/∂x.
Ako derivacije zx i zy, koje su također funkcije od x i y, imaju derivacije po x i y, bit će to djelomične derivacije drugoga reda funkcije z(x,y). Od zx potječu derivacije zxx, zxy; od zy derivacije zyx i zyy; imamo dakle
zxx = ∂2z/∂x2 = ∂zx/∂x; zxy = ∂2z/∂ ∂y = ∂zx/∂y;
zyx = ∂2z/∂y∂x = ∂zy/∂x; zyy = ∂2z/∂y2 = ∂zy/∂y.
Uz neke uvjete, koji su obično u primjenama ispunjeni, vrijedi, da je ∂z/∂x∂y = ∂'z/∂y∂x, da se dakle pri računu derivacije ∂'z/∂y∂x smije izmjeniti red, po kome se diferencira.
Sličnim se putom prelazi i na djelomične derivacije reda višega od drugoga i na derivacije funkcija, koje zavise od više nego dvije promjenljive. I za funkcije od više promjenljivih može se izvesti Taylorova formula, koja daje na pr. vrijednost funkcije z(x0+ h, y0 + k) kao zbroj jednoga polinoma stepena n-toga u veličinama h i k i ostatka. I ta je formula, kao za funkcije jedne promjenljive, izvor za diskutiranje ekstremnih vrijednosti funkcije, zakrivljenosti površina i drugih pitanja diferencijalne geometrije površina.
Implicitne funkcije. Iz izraza za potpuni diferencijal izlazi i pravilo, kako se traži derivacija funkcije jedne promjenljive, koja je zadana implicite, t. j. jednadžbom F(x,y)=0, koja nije riješena po y. Budući da je desna strana te jednadžbe identički jednaka nuli, bit će i njen potpuni diferencijal jednak nuli, t. j. Fxdx+Fydy=0, odakle izlazi za traženu derivaciju izraz:
dy/dx = — Fx/Fy.
Na pr. za funkciju x2+y2—1≡0, y'=—k2x/2y = — x/y.
Primjene diferencijalnoga računa. Sami osnivači d-a r-a, Newton i Leibniz (v.), primijenili su svoje nove metode na izučavanje svojstava krivulja i gibanja i otkrili onaj skup teorema, koji se i danas izvodi kao primjena toga računa. U znamenitom djelu Newtonovu Philosophiae naturalis principia mathematica (1687), u kome su izvedeni zakoni za gibanje nebeskih tijela iz zakona gravitacije, nađeni su najvažniji rezultati primjenom novih metoda računa fluksija, premda su predočeni za čitaoce u geometrijskom obliku. Primjene su se znatno proširile radom nasljedovatelja Leibniza i Newtona, napose braće Jakoba i Ivana Bernoulli-a (v.), l’Hospitala, koji je izdao prvu učevnu knjiga toga računa, a osobito L. Eulera (v.), s kojim se već prelazi u 18. st. Naročito je bila plodna misao, koja je vodila Leibniza i Newtona (a nadošli su na nju i neki suvremenici njihovi) do t. zv. obrnutoga ili inverznoga problema tangente, t. j. do određivanja svojstava krivulje iz svojstava tangente, pa istraživanja puta iz poznate brzine. Taj je problem vodio do integralnog računa (v.) i vezao u vrlo plodnu vezu ta dva područja infinitezimalnog računa (v.). Isti je problem i najjednostavniji primjer diferencijalne jednadžbe (v.), koja iz zadana odnosa među nepoznatom funkcijom jedne ili više promjenljivih i derivacija te funkcije, određuje sve funkcije, koje taj odnos zadovoljavaju. A kako veći dio primjena analitičkih metoda na proučavanje prirode vode do diferencijalnih jednačaba, bilo je time otvoreno opširno polje istraživanja, koje su sljedbenici Newtona i Leibniza sa zanosom i velikom vještinom i obradili i time stvorili matematičku fiziku, od koje je osobito mehanika neba pokazala svu dalekosežnost novih metoda.
LIT.: C. Jordan, Cours d’Analyse, 3 izd., sv. I.-III. Pariz 1909—15; E. Picard, Traité d’Analyse, 3. izd., sv. I.-III., Pariz 1922—28; É. Goursat, Cours d’Analyse mathématique, 4. izd., sv. I.-III., Pariz 1928; J. Hadamard, Cours d’Analyse, sv. I.-II., Pariz 1927—30; H. v. Mangoldt—K. Knopp, Einführung in die höhere Mathematik, 7. izd., sv. I-III., Leipzig 1943; R. Courant, Vorlesungen über Differential- und Integralrechnung, 2. izd., sv. I.-II., Berlin 1931; R. Rothe, Höhere Mathematik für Mathematiker, Physiker und Ingenieure, 6. izd., sv. I.-IV., Leipzig i Berlin 1940; G. Joos-Th. Kaluza, Höhere Mathematik für den Praktiker, 2. izd., Leipzig 1940; W. Nernst—A. Schoenflies, Einführung in mathematische Behandlung der Naturwissenschaften, 11. izd., München i Berlin 1931; H. Sirk, Mathematik für Naturwissenschaftler und Chemiker, 2. izd., Dresden 1941; J. Perry, Höhere Mathematik für Ingenieure, prev. R. Fricke—F. Süchting, 2. izd., Leipzig i Berlin 1910; G. H. Hardy, A course of pure mathematics, 5. izd., Cambridge 1928; F. Tricomi, Lezioni di analisi matematica, 4. izd., sv. I.-II., Padova 1939.
Jednostavan uvod daju G. Kowalewski, Einführung in die Infinitesimalrechnung, M. Lindow, Differentialrechnung; Integralrechnung, u zbirci Aus Natur und Geisteswelt, br. 197, 387, 673, Leipzig i Berlin; S. Škreblin, Infinitezimalni račun, Zagreb 1939.Ž. M.