 Sl. 1
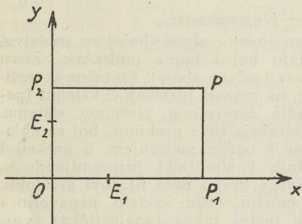
Sl. 1ANALITIČKA GEOMETRIJA. Grana geometrije (v.), koja proučava geometrijske objekte s pomoću matematičke analize (v.), dakle u zadnjoj liniji s pomoću računa; u opreci sa sintetičkom geometrijom (v.), koja se u istu svrhu služi ne računom, nego prostornim zrenjem, crtežima i modelima. Međutim nije anal. geom. na pr. izračunavanje opsega, površina i obujmova u običnoj planimetriji i stereometriji (v.) ili rješavanje geom. zadataka u trigonometriji (v.), jer u tim naukama nema onog pojma, koji je karakterističan za a. g., pojma naime koordinatâ. Svrha koordinata sastoji se u tome, da se od geom. objekata (točka, pravac, ravnina, krivulja, ploha i t. d.) prijeđe na analitičke (brojeve, jednadžbe i t. d.) i time se stave u službu geometrije sva mnogobrojna i snažna sredstva matem. analize. Do koordinata pak dolazimo ovako: U ravnini nacrtamo dva među sobom okomita pravca (v. sl. 1.), njihovo sjecište označimo slovom O, na jednom od njih odaberemo točku El, na drugom E2, ali tako, da je dužina OE1 = dužini OE2; ako je sada u toj ravnini zadana neka točka P, tada možemo njezino mjesto fiksirati s obzirom na tako konstruiranu figuru s pomoću dva broja na taj način, da točkom P povučemo paralele s čvrstim pravcima OE1 i OE2 do sjecišta P2 s pravcem OE2, odn. do sjecišta P1 s pravcem OE1, pak dužinu OP1 izmjerimo dužinom OE1, a dužinu OP2 dužinom OE2; tako dobivena dva broja označimo sa x odn. y:
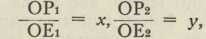
i zovemo ih: x apscisom, a y ordinatom točke P, zajedničkim imenom koordinatama te točke. To su dva neimenovana broja, koja nam posve jednoznačno određuju mjesto točke P u ravnini s obzirom na koordinatni sustav, t. j. na figuru, koja se sastoji od koordinatnih osi Ox (os apscisâ ili apscisna os) i Oy (os ordinatâ ili ordinatna os), ishodišta O te jediničnih točaka E1 i E2. Tako smo mjesto geometrijskog objekta, točke P, uveli analitički objekt, par brojeva (x, y), koji potpuno zastupa točku P. Velimo, da točki P ravnine korespondira par brojeva (x, y), a ta je korespondencija uzajmično (recipročno) jednoznačna, t. j svakoj točki P ravnine pripada samo jedan posve određeni par brojeva (x, y), ali i obrnuto, svakom paru brojeva (x, y) pripada u ravnini posve određena samo jedna točka P — sve dakako u nekom izvjesnom koord. sustavu. U drugom koord. sustavu imat će ista točka P neke druge koordinate x, y.
Uzmimo sada u ravnini neki neprekidni niz točaka, na pr. neku krivulju, koja je definirana geometrijski, t. j. tako, da je navedeno svojstvo zajedničko svim točkama te krivulje: na pr. kružnica kao niz točaka u ravnini, koje su jednako udaljene od jedne točke, ili elipsa kao niz točaka u ravnini, od kojih svaka ima svojstvo, da je zbroj njezinih udaljenosti od dvije čvrste točke stalan. To se bitno svojstvo dade izraziti analitički s pomoću jednadžbe, koju moraju zadovoljavati koordinate x, y svake točke te krivulje. U našim primjerima: Ako je kod kružnice ona čvrsta točka (središte) točka S (p, q), a ona stalna udaljenost (polumjer), r, tada se s pomoću Pitagorina poučka lako nađe, da koordinate svake točke P (x, y) kružnice moraju zadovoljavati jednadžbu
(x—p)2 + (y—q)2 = r2
i to je onda jednadžba te kružnice. Ako su kod elipse F1 (e, 0), F2 (—e, 0) one dvije čvrste točke (žarišta ili fokusi), a 2a (> 2e) onaj stalni zbroj udaljenosti (provodnicâ ili radij-vektora) F1P, F2 P točke P(x, y) elipse od točaka F1, F2, tada se može lako izvesti, da će koordinate x, y svake točke elipse morati zadovoljavati jednadžbu
gdje smo stavili, da je b2 = a2 — e2. To je jednadžba elipse. Tako se eto može za svaku geometrijski definiranu krivulju odrediti njezina jednadžba u općenom obliku f(x, y) = 0. A dalje je posao a. g., da iz te jednadžbe analitičkim postupcima i operacijama izvede sva svojstva pojedine krivulje. (U sintetičkoj geometriji dobivaju se ta svojstva bez koordinata i jednadžbi s pomoću posve geometrijskih razmatranja, dakako iz same geometrijske definicije odnosne krivulje, jer su u definiciji sadržana sva ta svojstva.)
Prema tome se bit analitičke geometrije može sažeti u ova tri njezina zadatka: 1. Zadani geometrijski problem treba prevesti u analitički govor (uvesti koordinate za pojedine točke, a jednadžbe za krivulje) na podlozi nekog koordinatnog sustava; 2. s tako dobivenim koordinatama i jednadžbama operira se po zakonima i postupcima matematičke analize, dakako u duhu i smislu postavljenog geometrijskog problema, i 3. dobiveni analitički rezultati tih operacija (koji su opet koordinate i jednadžbe) prevode se natrag u geometrijski govor, čime se dobiva traženo geometrijsko rješenje problema. Zgodnim izborom koordinatnog sustava može se postići, da jednadžbe, s kojima se radi, budu što jednostavnije, pak je onda analitičko operiranje spomenuto u točki 2. lakše.
Naprijed je prikazana bit anal. geometrije ravnine, t. j. dvodimenzionalnog ravnog operacionog prostora. Za analitičko rješavanje problema u prostoru vrijedi u principu sve isto, samo što treba uzeti kao podlogu koordinatni sustav u prostoru; to je onda anal. geometrija prostora. Tako imamo i anal. geometriju pravca kao jednodimenzionalnog ravnog operacionog prostora, a onda i anal. geom. četveroopćeno n-dimenzionalnog ravnog operacionog prostora. A sve se to još može generalizirati u tom smislu, da mjesto ravnog uzmemo neki zakrivljeni operacioni prostor (krivulju mjesto pravca, plohu mjesto ravnine i. t. d.), pak u njemu udesimo izvjesni koordinatni sustav i na njegovoj podlozi izgradimo analitičku geometriju toga zakrivljenog prostora. U svakom od tih različitih slučajeva ostaju analitičkoj geometriji ona tri bitna zadatka.
Pobliže o koordinatama i različitim njihovim vrstama → koordinate.
LIT.: Za početnika: Ganter-Rudio, Die Elemente der analytischen Geometrie, 2. sv., 10. odn. 7. izd., Leipzig 1927; opsežnija djela: Salmon-Fiedler, Analyt. Geom. der Kegelschnitte, 2 sv., 9. odn. 8. izd., Leipzig 1922 i 1930; Analyt. Geom. der höheren ebenen Kurven, Leipzig 1882; Analyt. Geom. des Raumes, 2 sv., 5. izd., Leipzig 1922/23 (original ovih triju djela je engleski); Heffter-Koehler, Lehrbuch der analyt. Geom., 3 sv., Leipzig 1905—1929, 2. izd. I. sv., Karlsruhe 1927; L. Bianchi, Lezioni di geom. analitica, Bologna 1923; B. Niewenglowski, Cours de Géométrie analytique, 4 sv., Pariz 1925—1929.
 Sl. 2
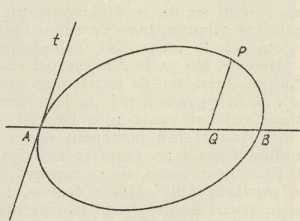
Sl. 2Historijat. Iz samog pojma analitičke geometrije, kako je gore prikazan, slijedi, da je za njezin postanak bilo potrebno dvoje: 1. jasno izrađeni pojam koordinata i 2. barem donekle izgrađena algebra kao prva etapa matematičke analize. Što se tiče koordinata, već su stari grčki geometri upotrebljavali nešto slično; u najsavršenijem obliku nalazi se to u Apolonijevim
konikama (→
Apolonije iz Perge). Tu je uzet jedan dijametar čunosječnice kao os (v. pravac AB u sl. 2), pak je bilo kojom točkom P čunosječnice povučena dužina PQ do te osi paralelno s tangentom t u krajnjoj točki A dijametra AB. Apolonije opisuje vezu između dužina AQ i QP samo riječima i to s pomoću proporcijâ; ta bi veza pisana u današnjem matem. označivanju bila upravo (tjemena) jednadžba te čunosječnice. Tu bi AQ=x, QP=y bile koordinate točke P u koord. sustavu, kojemu su osi dijametar AB i tangenta t. Ipak ih kod Apolonija još ne možemo smatrati koordinatama, jer je taj »koord. sustav« organički srastao sa samom krivuljom, te ona veza dužina AQ i QP izlazi samo kao individualno svojstvo te krivulje, a nipošto kao rezultat jedne općene metode ili općenog principa. Međutim sve kad bi to i bilo, ne bi mogla kod starih Grka nastati analitička geometrija zbog toga, što tada još nije bilo algebre u potrebnom obliku; a nije je moglo ni biti, jer stari Grci nisu imali posebnih znakova za brojke, nego su brojeve označivali slovima svoga alfabeta; zato su i ono nešto algebre, što su poznavali, zaodijevali u geometrijsko ruho. Tek kad je Francuz
Viète usavršio algebru, bio je ispunjen taj preduvjet za postanak anal. geometrije. Mnogi su geometri toga doba (konac 16. i početak 17. st.) uzeli primjenjivati algebru na rješavanje geom. zadataka (osobito planimetrijskih) i obrnuto, algebarske probleme nastojali riješiti s pomoću geom. konstrukcija, te se u tom poslu osobito istaknuo Dubrovčanin
Getaldić (v.). Ali to sve još nije bila analitička, nego neka algebarska geometrija.
Tek je Descartes u svom djelu La Géométrie izašlom 1637 dao bit anal. geometrije, jer je 1. dao pojam koordinata kao općenu metodu, općeni princip, uzevši za os apscisâ bilo koji pravac u ravnini (nezavisno o promatranoj krivulji), fiksiravši na toj osi čvrstu točku kao ishodište za mjerenje apscisâ te odabravši za to mjerenje jediničnu dužinu, i 2. jer se nije ustručavao primijeniti algebru na t. zv. neodređene zadatke, t. j. zadatke s neizmjerno mnogo rješenja, u kojima je naime ostajala jedna nepoznata veličina neodređena, dakle jedna koordinata slobodna, iz čega upravo rezultira jednadžba krivulje. Geometri prije Descartesa, među njima i Getaldić, namjerno su izbjegavali pobliže proučavanje ovakvih zadataka.
Ali, kao što se to desilo toliko puta u povijesnom razvitku matematike (na pr. iznašašće diferencijalnog i integralnog računa, neeuklidske geometrije i t. d.), tako je i ideja anal. geometrije dozorila i u jednog drugog geometra; to je Francuz Fermat, koji ju je izložio u raspravi Ad locos planos et solidos isagoge, štampanoj 1679, poslije smrti autora. Sigurno je, da je Fermat tu ideju imao izrađenu već prije 1637, ali prioritet iznašašća anal. geom. pripada Descartesu, jer je njegovo djelo prije publicirano.
Značenje anal. geometrije za razvitak matematike bilo je fundamentalno, jer je ona omogućila postanak i neslućeni razvoj infinitezimalnog računa, a time i svih ostalih grana matem. analize. Ova je pak za uzvrat poslužila anal. geometriji u njezinu daljnjem razvijanju.
Kao prvi nastavljači Descartesove ideje anal. geometrije treba da se spomenu de Beaune i van Schooten, a iza njih slijedi nepregledni niz drugih radnika na tom polju. Sam naziv »analitička geometrija« u današnjem njegovu smislu dao je Lacroix 1798, a prvi put se javlja u naslovu jedne knjige kod Garniera 1808. Modernu anal. geometriju izgrađivali su Gergonne, Bobillier, Lamé, Möbius, Plücker i Hesse.
BIBL.: R. Descartes, La Géométrie, novo izd., Pariz 1886; P. Fermat, Einführung in die enenen und körperlichen Örter, Leipzig 1923; A. F. Möbius, Der barycentrische Calcul, Leipzig 1827 (Gesammelte Werke, 1. sv., Leipzig 1885); J. Plücker, Analytisch-geometrische Entwicklungen, 2 sv., Essen 1828-1831; System der analyt. Geometrie, Berlin 1835; Neue Geometrie des Raumes, Leipzig 1868/69. R. C.