ELASTIČNOST (od novolat. elasticus od grč. ἐλαύνω »gonim, vučem«) ili pruživost, svojstvo plinova, da im možemo mienjati obujam time, što mienjamo tlak. Budući da kod tih promjena određenom obujmu kod jednakih temperatura pripada vazda jednak tlak, smatramo plinove savršeno elastičnima. Isto vriedi i za tekućine, ali kako su kod njih promjene obujma malene, obično se na elastičnost tekućina ne obaziremo. Kod puke promjene oblika ni kod plinova ni kod tekućina ne nastaju nikakve sile, koje bi ih vraćale u prijašnji oblik, pa su zato plinovi i tekućine s obzirom na oblik savršeno neelastični. Kruto tielo zove se elastičnim, jer u njem treba stvarati ili mienjati napetosti, ako želimo mienjati međusoban razmještaj njegovih česti. Ono bi bilo savršeno elastično, kada bi jednak razmještaj česti (kod jednakih temperatura) vazda nastao poradi jednakih napetosti.
1. Nauk o elastičnosti ili elastomehanika izpituje one mehaničke pojave krutih tjelesa, koji zavise o njihovoj elastičnosti. Taj se nauk započinje odkrićem, koje je Hooke priobćio najprije anagramom ceiiinosssttuu i onda 1678 riečima »ut tensio sic vis«, što iz latinskoga prevedeno znači: »kolika natega, tolika sila«. Taj Hookeov zakon tvrdi dakle, da je deformacija tiela razmjerna sili, koja ju proizvodi. U tom se obliku zakon može međutim primieniti samo u jednostavnim primjerima. Među njima je osobito znatan natezanje vertikalnog štapa (užeta, spirale i t. d.) utezom, koji na njemu visi. Ako je težina uteza P, a štap se produlji za Δl (l dužina štapa), po Hookeovu je zakonu
P = C ∙ Δl,
t. j. sila je razmjerna produženju, te na pr. za dvostruko produženje treba dvostruka sila. Napisana formula vriedi samo za pojedini štap, žicu i t. d., te svakomu primjerku odgovara drugi faktor razmjernosti C. Ona međutim obuhvaća i primjere, kad je štap odozdo poduprt, a utez ga odozgo pritiskuje. Δl u tom slučaju znači skraćenje štapa.
Obćenija formula dobije se, ako mislimo na štapove različitih dužina l, koji su svi izrezani kao dielovi jednog istog dugačkog štapa. Očekujemo, da utez P produljuje štap dvostruke dužine za dvostruko te je kod jednakih obterećenja kod tih štapova Δl razmjerno sa l. Omjer ε — Δl : l zove se specifično produženje; ako se štap stiska, specifično skraćenje ∙ ε = 1 značilo bi produženje na dvostruko ili skraćenje na dužinu 0 (fiktivno). Uvodeći ε Hookeov zakon glasi:
P = D ∙ Δl/l = D ∙ ε
t. j. sila je razmjerna specifičnom produženju, dotično specifičnom skraćenju.
2. Youngov modul. Još obćeniji oblik zakona dobiva se, ako mislimo na štapove različitih dužina i različitih proreza, a iste tvari, na pr. na štapove od iste vrsti bakra. Djelovanje sile P bit će to manje, što je veći prorez štapa ω, i dva štapa od iste tvari, jednakih dužina, a različitih proreza jednako će se produljiti, ako kod svakog štapa na jedinicu površine proreza odpada jednak dio sile, naime p, gdje je p = P : ω. Taj se omjer zove vlak, kada štap raztežemo, a tlak, kada ga stiskamo. Onda vriedi za koji god štap P = E ∙ ω ∙ Δl : l ili kraće
p = E ∙ ε, (1)
t. j. vlak, dotično tlak razmjeran je specifičnom produženju, dotično specifičnom skraćenju. Za štapove od iste tvari faktor E je isti. On je puka »materialna« konstanta i može se naći u fizikalnim tablicama, a zove se Youngov modul ili modul elastičnosti (lat. modulus »mjera«). Potonji izraz (Young, 1807) manje je zgodan, jedno, jer taj modul sam za se ne dostaje da prikaže elastična svojstva tiela, drugo zato, što je E maleno baš kod tjelesa, koja smatramo veoma »elastičnima«, na pr. kod kaučuka.
Primjer: Za neku vrst čelika je E = 22000 kg*/mm2; ako je žica od tog čelika duga 1000 mm, a prorez joj je 2 mm2, i želimo je produljiti za 1 mm, trebat će žicu natezati silom P, koja izlazi iz p = P : 2 = 22000 ∙ 1 : 1000, dakle P = 44 kg*. Za neku vrst olova je E = 1700, za mekani bakar 10500, staklo 5000 do 8000. Svi ti brojevi vriede kod obične temperature, kod drugih je temperatura i E drugo.
Kod anizotropnih tvari, t. j. onakvih, koje u različitim smjerovima imadu različita svojstva, ne postoji samo jedan Youngov modul, već je taj modul različit za štapove, koji su iz tvari izrezani u različitim smjerovima. Ipak za kovine, kao na pr. čelik, premda se sastoje od ledaca, Youngov je modul samo jedan, i to zato, jer su sićušni ledci, iz kojih se takva tvar sastoji, upravljeni prosječno jednako na sve strane, te tvar u krupnom ne pokazuje anizotropije.
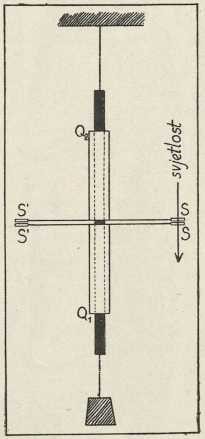 Sl. 1.
Sl. 1.Kako je mienjanje dužine štapa pri obterećivanju neznatno, nije lako mjeriti ga, pogotovu, ako je štap kratak, i ako ga ne smijemo jače obteretiti. Osobito je osjetljiv postupak mjerenja s pomoću pojava interferencije svjetlosti. Da kod štapa izmjeri raztezanje komada, koji seže od proreza Q1 do proreza Q2 (sl. 1), Grüneisen 1907 učvršćuje na štap kod Q1 donji kraj jedne cievi, koja obuhvaća štap do blizu njegove polovice, a svršava se vodoravnim prstenom; isto tako se kod Q2 učvrsti gornji kraj druge takve cievi. Prstenovi drže kod S svaki po jednu staklenu ploču, tako da je među pločama planparalelan sloj uzduha, koji je 2 do 3 mm debeo. Koliko se komad štapa, koji seže od Q1 do Q2, raztezanjem produlji, za toliko postane sloj uzduha deblji. Oba su stakla, gdje graniče s tim slojem, poluposrebrena, da svjetlost dielom propuštaju, dielom odbijaju, pa ako se kroz stakla pušta svjetlost dužine vala λ, nastaje Heidingerov pojav interferencije: svietle »krivulje jednakog priklona«. Ti se krugovi suzuju, kada debljina sloja raste, pa kad se spomenuti komad štapa raztegne za λ : 2, svaki se svietli krug stegne na mjesto, gdje je bio iznutra susjedni. Kako je λ maleno i dobro poznato, na pr. 0∙0005461 mm kod zelene živine svjetlosti, mogu se izmjerivanjem toga pojava i sićušne promjene dužine točno odrediti. Osim stakala S prstenovi radi kontrole nose na suprotnoj strani još jedan takav par stakala S', pa se tu mjerenje ponovi.
3. Granice Hookeova zakona. Kod prevelikoga obterećenja Hookeov zakon prestaje valjati, pa se najveća vriednost vlaka, dotično tlaka, do koje zakon vriedi, zove granica razmjernosti. Bude li obterećenje veće, produženje dotično skraćenje izlazi veće, nego što bi sliedilo iz Hookeova zakona. Amo se možda može ubrojiti i zanimljiv slučaj livenog željeza, za koje je Hodgkinson 1849 našao da se ni kod najmanjih obterećenja ne vlada po zakonu razmjernosti. Iznad granice razmjernosti dolazi granica elastičnosti. Ako štap podvrgnemo vlaku, koji je iznad granice elastičnosti, pa onda vlak uklonimo, štap se ne će vratiti na prvobitnu svoju dužinu, nego će ostati nešto dulji, no što je bio prije obterećenja. Do granice elastičnosti on se vladao kao savršeno elastično tielo. Tako se na pr. kod nekog čelika našla granica elastičnosti kod vlaka 33 kg*/mm2; kod olova ta je granica daleko manja. Ustalom, gdje će se naći granica e-i, zavisi o točnosti, kojom opažamo. Često se uzme za granicu ono obterećenje p, poslije kojega štap pokazuje specifično produženje ε = 0∙00003, t. j. Δl = 0∙003%l, dakle t. zv. 0∙003%-granica.
Ima primjera, kod kojih doduše pri krupnijem mjerenju Hookeov zakon izlazi valjan, dok se uz veću točnost nađe, da jednakom vlaku odgovara manja dužina štapa, kada se do tog vlaka došlo povećavanjem vlaka, nego kada je on nastao iza većih vlakova. Taj se pojav radi sličnosti s magnetskim histerezom zove elastična histereza (Cantone, 1893; Bouasse, 1897). Važan su pojav elastični naknadni učinci. Pri natezanju štapa oni se očituju dvojakim načinom. Jedno time, da neko obterećenje ne izvede odmah konačno produženje, već, ako čekamo, produživanje još neznatno napreduje, i tekar iza dugog vremena dužina štapa bude stalna (W. Weber, 1835). Drugo je t. zv. relaksacija, pojav, da za neko produženje treba izprva veći vlak, a ako ne ćemo, da produženje i dalje raste, treba vlak kroz neko vrieme sve više smanjivati.
Kao kod natezanja štapova treba i kod drugih vrsti deformacija očekivati slična ograničenja za valjanost Hookeova zakona, te na pr. relaksaciju nalazi kod torzije F. Kohlrausch 1863.
4. Poissonov broj. Kada se štap ili žica vlakom produže, prorez im se smanji. Time se svaka dužina u prorezu smanji. To skraćivanje u poprečnom smjeru lako se primjećuje na pr. kod kaučukove vrpce, koja se da veoma produljiti. Kako je debljina d štapa redovno malena prema dužini, bit će smanjenje debljine Δd osobito maleno, ali specifično skraćenje kojegod dužine u prorezu, ili kraće: specifično poprečno skraćenje δ = Δd : d uobće ne zaostaje baš mnogo za specifičnim produženjem štapa ε. Obrnuto: pri stiskanju štapa nastaje specifično skraćenje dužine štapa i povećanje debljine njegove. Ako su δ i ε malene veličine, njihov je omjer μ = δ : ε (2) konstantan i zove se Poissonov broj. On je odigrao vidnu ulogu u poviesti teorije elastičnosti. Prema starijim teorijama (Navier, Poisson, Cauchy i t. d.), koje su kao osnov razmatranja uzimale »Boškovićansko« elastično tielo (taj naziv uvodi Lord Kelvin u Baltimore Lectures) i pomišljale, da su tjelesa sastavljena od tvarnih točaka, koje u daljinu djeluju jedne na druge, izlazilo je, da je μ za sve izotropne tvari isto i jednako ¼. Protivnici te tvrdnje mogli su pokazati primjere, koji je pobijaju. Tako je kod kaučuka μ = ½, a štap od pluta produživanjem uobće ne mienja poprečnih protega, te mu je μ = 0. No taj su prigovor pristaše omjera ¼ odbijali s tvrdnjom, da i pluto i kaučuk imadu šupljina, te nisu dovoljno homogen material, koji bi dao pouzdan rezultat. Uostalom, izašlo je i za druge tvari μ različno od ¼ te je na pr. za bakar 0∙35, olovo 0∙45, staklo 0∙2 — 0∙3 i t. d. A našli su se (ali samo kod ledaca) i primjeri, gdje je μ negativno, što će reći, da se produženjem štapa, načinjenog iz takve tvari, poveća i debljina njegova. Tako je Voigt (v. 12) izveo mjerenja na piritu, iz kojih izlazi, da štapić, izrezan iz piritova ledca u smjeru kristalografske osi, imade μ = —0∙15.
5. Stlačivost. Ako je za neku tvar poznat Youngov modul E i Poissonov broj μ, može se izračunati i njezina stlačivost ili kompresibilnost k. Da se odredi taj pojam, zamislimo, da smo obujam V kojegod tvari izložili tlaku sa svih strana jednaku, p, te se obujam smanjio za ΔV. Omjer ΔV : V (smanjenje obujma 1) zove se specifično smanjenje obujma. Omjer toga omjera i tlaka p zove se stlačivost
k = ΔV/V : p
(3)
Da se nađe sveza veličine k sa E i μ, zamislimo tielo u obliku kocke. Kocka se može smatrati štapom, koji je toliko debeo, koliko dug. To ide na tri načina, prema tome, koji smjer u kocki uzmemo za dužinu štapa. Ako kocku stiskamo sa svih strana jednako, možemo dakle trokratnom primjenom Hookeova zakona i uzimajući svaki put u obzir poprečno raztezanje naći, da specifično skraćenje brida kocke iznosi p (1 —2μ) : E. Ako je to skraćenje maleno, izlazi za specifično smanjenje obujma ΔV : V = 3p (1—2μ) : E, dakle prema definiciji stlačivosti
k = 3 (1-2μ)/E. (4)
Kada bi za neku tvar bio Poissonov broj μ = ½, bila bi stlačivost k = 0, te se toj tvari tlakom ne bi mogao smanjiti obujam (vriedi približno kod kaučuka). Budući da nije poznata tvar, kojoj bi tlakom obujam narastao, k ne može biti negativno. Prema tome μ ne može biti veće od ½.
Stlačivost čelika je 0∙00006 mm2/kg*, olova 0∙00023, stakla 0∙00013—0∙00029 (sve kod 18°C; kod te temperature stlačivost je vode 0∙005). Prema tome tlak 1 kg*/mm2 (= 100 tehničkih atmosfera) smanjuje 1 dm3 čelika za 0∙00006 dm3 = 0∙06 cm3.
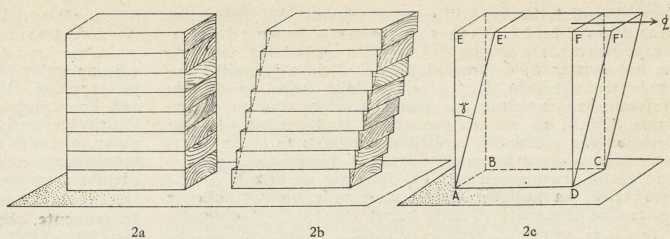 Sl. 2.a i 2. b. Model za deformaciju
Sl. 2.a i 2. b. Model za deformaciju
zvanu klizanje Sl. 2c. Klizanje6. Modul klizanja. Osim E, μ i k često se upotrebljava i modul klizanja ili »drugi« modul elastičnosti G. Određuje se uz pomoć pojma klizanja ili smicanja. To je deformacija, koja se da objasniti modelom sagrađenim iz knjiga ili daščica. Vodoravne jednake, četverokutne, tanke daščice slože se u uzpravnu prizmu (sl. 2a). Zatim ostavimo najdonju daščicu, osnovku prizme, na miru, a druge sve pomaknimo klizanjem, tako da od uzpravne prizme postane kosa prizma (sl. b). Pomišljamo, da su daščice tako tanke, da se stube u kosoj naslazi daščica ne primjećuju. Umjesto toga modela uzmimo sada jedan jedini prizmatički komad krute tvari (sl. c). Donja osnovka ABCD te prizme neka je na podlogu učvršćena, a na gornju neka djeluju sile nadesno, uzporedno bridu EF i jednolično porazdieljene, tako da na svaki mm2 gornje osnovke djeluje jednaka sila. Pod utjecajem tih tangencialnih sila elastično tielo popušta te se izobliči, pri čemu se vodoravni slojevi tiela pomaknu kao daščice u modelu. Brid EF pomakne se sam u sebi i dođe u namještaj E'F' =EF. Očito je, da se kod te deformacije obujam tiela ne mienja. Veličina izobličenja dana je kutom klizanja γ = EAE', i ako je taj kut malen, što gotovo uviek biva, on je jednak EE' : AE radian (1 radian = 57°18').
Klizanje, prikazano u sl. c, nije puka ili »čista« deformacija. Kada je pravokutnik ABFE prešao u paralelogram ABF'E', brid AB ostao je na svome mjestu, dok se brid AE zakrenuo za kut γ. Prema tome treba uzeti, da se prigodom deformacije četverokut ABFE kao cjelina zakrenuo za kut γ : 2, koji je zakret deformaciji pridružen.
Nastala je ta deformacija poradi tangencialne napetosti ili naprezanja q, koje se sračunava, ako se ukupna sila Q, što djeluje na gornju osnovku, podieli s površinom ω te osnovke, t. j. q = Q : ω. Prema Hookeovu zakonu treba sada staviti
q = G ∙ γ,(5)
gdje se faktor razmjernosti G zove modul klizanja. Treba odmah dodati, da primjer klizanja ne nalazimo kod samoga Hookea. Tu deformaciju razmatra Young 1807, a modul klizanja definira tekar Navier 1833. Kod torzije (sukanja) valjka ili žice prorezi se valjka skližu jedni uz druge oko osi valjka. (Pri tom je klizanje u samoj osi valjka 0, a uz plašt njegov najveće.) Zato se G može odrediti izmjerivanjem torzije i sila, koje ju izvode. Za čelik je G = 8300 kg*/mm2.
Od četiri veličine E, G, μ i k prve dvie imadu dimenziju kao i tlak, t. j. [sila : ploha], μ nema dimenzije, dok je za veličinu k dimenzija [ploha : sila].
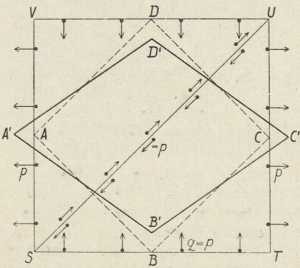 Sl. 3. Kada se kocka STUV izobliči vlakom
Sl. 3. Kada se kocka STUV izobliči vlakom
p i tlakom q=p, deformacija je klizanje7. Jednačba među modulima. Da se nađe, kako je modul klizanja povezan s Youngovim modulom, može se izpitati ovaj primjer. Kocka, prikazana kvadratom STUV (sl. 3), neka se u smjerovima ST nateže vlakom p, koji djeluje na lievu površinu kocke SV i na desnu TU. U smjerovima SV neka se kocka stiska tlakom q = p, koji djeluje na donju površinu ST i gornju VU. Na prednju površinu STUV i stražnju (u slici opet STUV) neka ne djeluje nikakva sila. Pod utjecajem takvih sila kocka se produlji u smjeru ST, a skrati u smjeru SV. Primjenjujući dvaput Hookeov zakon za štap dobivamo specifično produženje ε = p(l + μ) : E i isto toliko specifično skraćenje. Za rješenje zadaće treba još jedan podatak o napetosti u nutarnjosti kocke, i to: kakvom silom utječu jedan na drugi dva diela kocke, koji se tiču u ravnini SU položenoj kroz brid S i brid U. Ta ravnina razstavlja kocku u dvie trostrane prizme. Da prizma STU bude u ravnotežju, treba da na nju prizma SVU kroz plohu SU djeluje jednoliko porazdieljenim silama. Za te se sile lako nađe da djeluju smjerom tangencialnim na plohu, a uzporedne su osnovkama STUV, pa ako se sveukupna tangencialna sila, što djeluje kroz plohu SU, podieli s veličinom te plohe, izlazi tangencialna napetost opet jednaka p. (Jednakim i protivnim silama djeluje prizma STU kroz SU na prizmu SVU.) Isto vriedi za kojugod drugu unutarnju plohu, koja je uzporedna plohi SU ili koja je na SU i STUV okomita.
U kocki STUV sadržana je prizma, kojoj je osnovka kvadrat ABCD, kojemu su diagonale uzporedne i jednake bridovima kocke. Izobličenjem kocke dužina se tih diagonala promieni kao i dužina kockinih bridova, te od lika ABCD nastane romb A'B'C'D'. Budući da su pomaci točaka A, B, C i D maleni i jednaki, dade se pokazati, da se površina kvadrata deformacijom nije promienila, i da je deformacija spomenute prizme klizanje. To se klizanje razlikuje od klizanja, prikazanog u sl. 2, time, što je tamo deformaciju pratio zakret tiela, dok je ovdje izobličeno tielo simetrično namješteno prema prvobitnome svom namještaju, pa se tu radi o čistoj deformaciji, bez zakreta. Za veličinu toga klizanja izlazi γ = 2ε = 2 ∙ p ∙ (1 + μ) : E. U drugu ruku, budući da se to klizanje može shvatiti kao učinak (tangencialnih) napetosti p, koje djeluju kroz plohe AB, BC, CD i DA, vriedi za γ još i jednačba (5), t. j. γ = p : G. Izpoređivanjem obaju izraza za γ izlazi dakle tražena sveza konstanata
G = E/2 (1 + μ)(6)
Kao što je formula (4) dala gornju granicu za Poissonov broj, tako ova formula pokazuje, da Poissonov broj mora biti svakako veći od —1. Kada bi μ bio manji od —1, bilo bi naime G negativno, te bi u tvari s takvim μ klizanje nastalo u smjeru, koji je protivan smjeru sila.
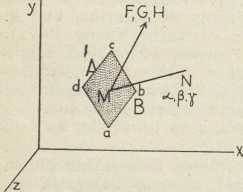 Sl. 4. A djeluje na B kroz abcd
Sl. 4. A djeluje na B kroz abcd
(okomica MN) napetošću F, G, H8. Analiza napetosti. Napetost ili naprezanje u unutarnjosti elastičnog krutog tiela zamršeniji je pojam od tlaka u mirnoj tekućini. Izgradnju toga pojma zahvaljujemo Cauchyju (1822). Da se upozna napetost u točki M tiela, položi se u misli kroz tu točku komad plohe abcd (sl. 4) malene veličine ω i odredi, kako djeluju kroz tu plohu jedan na drugi dielovi A i B tiela, koji se u toj plohi dotiču. Po trećemu Newtonovu aksiomu sila, kojom A djeluje na B, jednaka je i protivna sili, kojom B djeluje na A. Kao kod tlaka i kod tangencialne napetosti, tako nas i ovdje zanima omjer sile i plohe (t. j. sila, koja djeluje kroz plohu 1), pa taj omjer zovemo napetost kroz plohu abcd. Za plohu treba onda zamišljati redom sve moguće orientaciie i svaki put odrediti napetost, koja kroz nju djeluje. Skup svih podataka, tako dobivenih, označuje onda fizikalnu veličinu, koja se zove naprosto napetost u točki M. Kod mirne tekućine za svaki namještaj plohe izlazi napetost jednaka, a njezin smjer okomit na plohu. Kod krutog tiela jedno i drugo samo iznimice vriedi, te napetost uobće zavisi o orientaciji plohe abcd. Ta se određuje tako, da se načini pravac MNabcd i naznači, koje kutove čini ta okomica s osima x, y, z pravokutnog koordinatnog sustava, dakle α = Nx, β = Ny, γ = Nz. Sama napetost razstavi se u tri komponente F, G, H, koje su redom uzporedne koordinatnim osima x, y, z. Spomenute komponente mogu se onda izračunati iz orientacije plohe abcd i 6 veličina
Xx, Yy, Zz, Yz = Zy, Zx = Xz, Yy = Yx; (7)
vriede naime relacije
| F = Xxcosα + Xycosβ + Xzcosγ |
| G = Yxcosα + Yycosβ + Yzcosγ |
| H = Zxcosα + Zycosβ + Zzcosγ |
(8)
Što veličine (7) znače svaka za se, sliedi iz samih formula (8). Ako je ploha abcd uzporedna ravnini yz, te je α = 0°,
β = γ = 90º, izlazi F = Xx, G = Yx, H = Zx. Dakle je Xx normalna komponenta napetosti, jer ona smjerom osi x djeluje kroz plohu okomitu na x, te veliko slovo X upućuje na smjer komponente, a kazaljka (indeks) x na orientaciju plohe. Yx je tangencialna komponenta napetosti; ona kroz plohu, okomitu na x, djeluje smjerom y i t. d. Cauchyjev rezultat Yz—Zy znači prema tome, da kroz plohu, okomitu na smjeru z, djeluje u smjeru y isto tolika komponenta napetosti, kolika kroz plohu, okomitu na y, djeluje u smjeru z.
Kako kod mirne tekućine napetost nema tangencialne komponente, kod nje je Yz = Zx= Xy = 0, F = Xxcosa, G — Yycosβ, H = Zzcosγ, pa budući da mora kroz svaku plohu abcd napetost djelovati smjerom normale MN, treba da je F : G : H = cosα : cosβ : cosγ, dakle je Xx = Yy= Zz =
, te je tlak (ili vlak) kod mirne tekućine u svim smjerovima jednak.
Predznaci veličina (7) u literaturi određuju se dvojako. Zamislimo, da je ploha abcd okomita na osi x, i da polazeći iz područja A u B idemo pozitivnim smjerom te osi, onda se predznaci veličina Xx, Yx, Zx određuju bilo prema predznacima sila, kojima A djeluje na B, bilo prema predznacima sila, kojima B djeluje na A. Slično vriedi za 3 preostale veličine (7). Kod prvog načina, koji će se i ovdje primieniti, tlak je pozitivan, vlak negativan, kod drugoga tlak je negativan, vlak pozitivan.
Iz jednačbi (8) dade se zaključiti, da se i u najobćenijem slučaju kroz svaku točku M elastičnog tiela mogu položiti tri međusobno okomite ravnine, kroz koje napetosti djeluju okomito na te ravnine. Te se tri ravnine zovu glavne ravnine napetosti, a napetosti, koje kroz njih djeluju, zovu se glavne napetosti. Njihovi smjerovi zovu se glavne osi napetosti. Glavne napetosti mogu biti ili tlaci ili vlaci, dakle pozitivne ili negativne. U primjeru sl. 3 glavne su napetosti p, -p, 0. Kada štap stiščemo smjerom dužine, izlaze glavne napetosti p, 0, 0. Takve su unutarnje napetosti u tim primjerima, ako napetosti potječu samo od sila, kojima izvana djelujemo na tielo. Moguće je međutim, da postoje unutarnje napetosti u tielu i bez izvanjih sila; na pr. napetosti u naglo hlađenom staklu ili napetosti u tielu poradi nejednakih temperatura.
Dobar pregled napetosti u nekoj točki M dobiva se, ako se koordinatni sustav tako namjesti, da se glavne ravnine napetosti podudaraju s koordinatnim ravninama. Onda je Yz = Zx = Xy = 0, a Xx, Yy i Zz jesu glavne napetosti. Ploha drugoga stupnja (elipsoid i t. d.)
Xx ∙ x2 + Yy ∙ y2 + Zz ∙ z2 = ± 1, (9)
t. zv. ploha napetosti, jednostavno upućuje, koji je smjer i koja veličina napetosti za kojugod plohu položenu kroz točku M. Okomica Mn (sl. 5.) takve plohe produlji se, da sieče plohu napetosti, i u presjecištu A načini se tangencialna ravnina TT. Njezina okomica AN daje smjer napetosti, p // AN. Normalna pak komponenta napetosti pn obrnuto je razmjerna kvadratu radija vektora; pn = l : MA2. U primjeru sl. 3 plohu napetosti čine dva (± 1) konjugirana hiperbolična valjka; kod natezanja štapa ploha napetosti degenerira u dvie uzporedne ravnine.
Nauk o fotoelastičnosti eksperimentalno izpituje napetost u elastičnom tielu, i to s pomoću dvoloma svjetlosti, koji poradi napetosti nastaje u modelu onoga tiela načinjenom od prozirne tvari (→ dvolom, 2).
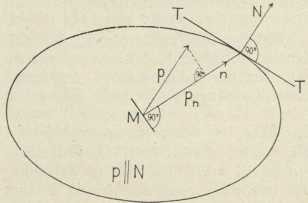 Sl. 5. Ploha napetosti pokazuje sve smjerove i veličine
Sl. 5. Ploha napetosti pokazuje sve smjerove i veličine
napetosti u točki M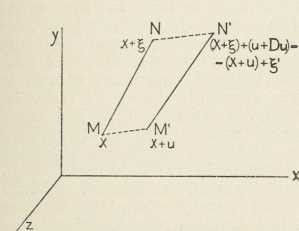 Sl. 6. Izobličenjem tiela dužina MN
Sl. 6. Izobličenjem tiela dužina MN
pelazi u M' N'9. Nacrt dinamičkih jednačbi. Kod deformacije elast. tiela čestica, koja je izprva imala koordinate x, y, z, neka je pomaknuta u smjeru osi x za dužinu u, u smjeru y za v, u smjeru z za w, tako da su joj nove koordinate x + u, y + v, z + w. Nauka o elastičnosti u prvom redu razmatra zadaće, u kojima su u, v, w maleni. Onda vriede dinamičke jednačbe (Cauchy, 1827).
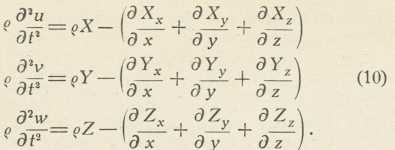
U tim jednačbama ϱ znači gustoću tiela na mjestu s koordinatama x, y, z. Drugi diferencialni kvocienti po vremenu t jesu komponente akceleracije čestice, koja je na tome mjestu. Lieve su dakle strane umnožci mase, preračunane na obujam 1, s tima komponentama. Po zakonima dinamike ti su umnožci jednaki komponentama sila. Jedne sile izvana neposredno djeluju (→ djelovanje u daljinu). Ako masu 1 tjera sila s komponentama X, Y, Z, preračunane na obujam 1 te su komponente ϱX, ϱY, ϱZ. Izrazi u zagradama jesu komponente sila, koje se rađaju od elastične napetosti, budući da se komponente napetosti Xx,... od mjesta do mjesta mienjaju.
U jednačbama (10) umjesto predznaka — na desnoj strani treba da stoji +, kada se predznak napetosti određuje obrnutim načinom, nego što je ovdje učinjeno. Kako napetost zavisi o samim pomacima, jednačbe (10) uobće nisu dovoljne za rješavanje zadaća. One su tek izhodište za daljnje izvode. Kada se radi o zadaćama statičkima, lieve strane jednačbi treba staviti =0.
10. Analiza deformacije. Ako se točka M s koordinatama x, y, z poradi deformacije pomakla u M' (sl. 6) te je dobila koordinate x + u, y + v, x + w, susjedna točka N, koja je prije deformacije imala koordinate x + ξ, y + η, z + ξ, dobit će druge pomake, t. j. ona će se pomaći do N', i to u smjeru x za iznos u + Du, u smjeru y za v + Dv, u smjeru osi z za w+Dw, gdje je Du=
+
+
Dv = ∙∙, Dw = ∙∙ . To vriedi, ako je točka N blizu M. Točka N' ima dakle koordinate (x + ξ) + (u + Du),∙∙, ∙∙. Kada bi se prije deformacije uzela točka M za početak koordinata, imala bi točka N koordinate ξ, η, ζ. A ako se poslije deformacije uzme M' za početak, točka N' dobiva koordinate ξ = x + ξ + u + Du —(x + u) = ξ + Du, η'=η + Dv, ζ' = ζ + Dw, dakle
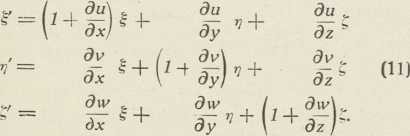
Te nam formule za svako ξ, η, ζ daju skup vriednosti ξ', η, ζ, t. j. za svaku dužinu MN neizobličenog tiela kazuju njezin smjer i veličinu M'N' iza deformacije. Kako su te jednačbe linearne, one predočuju t. zv. homogenu deformaciju. Za nju se da pokazati, da uzporedne ravnine (pravci) ostaju i poslije deformacije uzporedne, da se dvie uzporedne dužine deformacijom jednako produlje, da kugla deformacijom prelazi u elipsoid i t. d. Kako god ξ, η, ζ u jednačbama (11) imadu 9 uobće različitih koeficienata, ipak se može pokazati, da je deformacija dana samo sa 6 veličina. U tu svrhu treba uvesti 9 veličina, dotično kratica
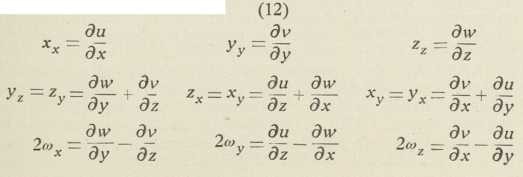
Time jednačbe (11) primaju oblik (13)
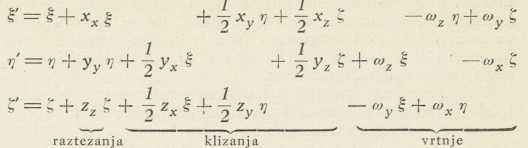
Da se razabere značenje novih koeficienata, zamislimo najprije, da svi ti koeficienti osim xx budu jednaki 0. Onda bi deformacija bila dana jednačbama ξ' = (1 + xx) ξ, η' = η, ζ' = ζ. To znači, da bi sve točke N u okolišu točke M bile pomaknute samo u smjeru x, i da bi pomak bio to veći, što je veće MN. Pri tom jednolikom raztezanju xx znači specifično produženje, dotično specifično skraćenje, ako je xx negativno. Slično značenje imadu yy s obzirom na smjer y i zz s obzirom na smjer z. Ako je od veličina (12) samo yz različno od 0, deformaciju prikazuju jednačbe
ξ' = ξ, η' = η +
yz ζ, ζ' = ζ +
zy η.
Ta se deformacija može razstaviti u dvie: najprije se slojevi, uzporedni ravnini xy, skližu smjerom y, a zatim se slojevi, uzporedni ravnini xz, skližu smjerom z. Rezultujući je kut klizanja
yz +
zy = yz.
Od ta dva klizanja sastavljena deformacija jest bez rotacije, dakle kao u sl. 3, a ne kao u sl. 2. Slična značenja imadu veličine zx i xy. Najposlije, kada bi od onih koeficienata bio samo ωx različan od 0, nove bi koordinate bile povezane sa starim jednačbama ξ' = ξ, η' = η—ωxζ ζ' = ζ + ωxη, a te jednačbe znače, kako se lako može pokazati, puku vrtnju okoliša točke M oko osi uzporedne osi x. To dakle nije deformacija, i ta promjena namještaja točaka ne izazivlje napetosti. Prema tome izlazi, da se sva promjena, prikazana jednačbama (11) dot. (13), sastoji od 3 jednolika raztezanja, 3 klizanja bez vrtnje i od 3 vrtnje. Da te pojedinačne promjene, redom izvedene, daju za rezultat promjenu (11), sliedi odtuda, što su veličine xx,∙∙∙∙∙ — kako to predpostavljamo — malene. Kada to ne bi bilo, onda bi deformacija, koja bi nastala iza postepenog izvođenja spomenutih jednostavnih promjena, bila mnogo zamršenija i zavisila bi o tom, kojim smo redom pojedina raztezanja, klizanja i vrtnje izvodili. Čista je deformacija dakle dana sa 6 veličina xx, yy, zz, yz, zx, xy, kako je i to Cauchy upoznao, pa se te veličine zovu komponente deformacije, bez obzira na to, ima li vrtnje ili nema. Po broju komponenata deformacija se dakle vlada kao i napetost. Jednu i drugu ubrajamo među fizikalne veličine, što ih zovu tenzorima.
Obćenito vriedi, da se kroz koju god točku M deformiranoga tiela dadu položiti tri međusobno okomita pravca, koji su bili jedan na drugom okomiti i prije deformacije. To su glavne osi deformacije. Ako koordinatne osi tako namjestimo, da su uzporedne glavnim osima deformacije, onda je yz = zx = xy = 0, a xx, yy, zz, specifična raztezanja u smjerovima x, y, z zovu se glavna specifična raztezanja. Veličina xx + yy + zz =
nekoj točki M vazda jednaku vriednost, kako god zakrenemo osi koordinatnog sustava. Ta invarianta znači specifični prirast obujma čestice oko točke M.
11. Poobćeni Hookeov zakon, I. Jednačbama (1) i (5) prikazan je Hookeov zakon u dva jednostavna, ali važna primjera, gdje su izobličenje i napetost određeni po jednom veličinom. Pitanje je, kako zavisi napetost obćenije vrsti, koja je dana sa 6 komponenata Xx,∙∙∙∙∙, o izobličenju, koje je također opisano sa 6 komponenata xx, ∙∙∙∙∙. Za taj obćeni slučaj elastomehanika nalazi, da između jednih i drugih veličina postoji 6 jednačbi prvoga stupnja, poobćenje Hookeova zakona:
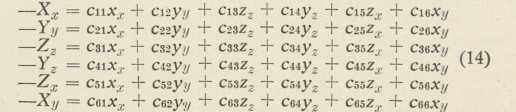
sa 36 »elastičnih konstanata«. Prva kazaljka (indeks) svake konstante kazuje, u kojoj jednačbi konstanta dolazi, dok druga kazaljka naznačuje komponentu deformacije, pred kojom konstanta stoji. Tako je na pr. c35 u 3. jednačbi 5. konstanta. Teoretski izlazi, da je chk = ckh, to će reći, da je k-ta konstanta h-te jednačbe jednaka h-toj konstanti k-te jednačbe. (V. 12.) Od 36 konstanata preostaje dakle samo 21 različita.
Kod izotropnih tvari broj se konstanata smanjuje na 3, i od tih su samo 2 nezavisne, tako da poobćeni Hookeov zakon za izotropno tielo glasi
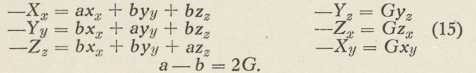
To stezanje broja konstanata izlazi iz ovih razmatranja.
1. Kod izotropnog tiela treba uzeti, da se glavne osi napetosti podudaraju s glavnim osima deformacije. Ako su dakle glavne osi deformacije uzporedne koordinatnim osima, te je yz = zx = xy = 0, onda su i 3 posljednje komponente napetosti Yz = Zx = Xy = 0, i to kraj svih mogućih vriednosti glavnih raztezanja xx, yy, zz. To je samo tako moguće, ako 3 prve konstante 4., 5., i 6. jednačbe (14) budu jednake 0, dakle c41 =∙∙∙∙= c63 = 0.
2. Ako je xx = yy = zz = zx = xy = 0, a samo yz je različno od 0, te je deformacija puko klizanje okomito na os x, onda za svaku vriednost yz izlazi Xx = Yy = Zz = Zx = Xy = 0, a —Yz = G yz prema jednačbi (5) (za predznak v. 8). To je opet samo moguće, ako je c14 = c24 = c34 = c54 = c64 = 0 i c44 = G.
Slično se pokazuje, da je c55 = c66 = G, i da su sve druge konstante pred 5. i 6. komponentom deformacije = 0.
3. Najposlije, ako je Xx glavna napetost, ona treba da zavisi o specifičnom produženju istoga smjera xx jednako kao i Yy o yy ili Zz o zz, te je c11 = c22 = c33 ili s kraćom oznakom = a. I onda: Xx zavisit će o specifičnom produženju okomitog smjera yy jednako kao i o zz, te je c12 = c13 = b, i t. d. Tako je prvih 6 jednačbi (15) objašnjeno.
4. Da se dokaže i 7. od tih jednačbi, zamislimo štap smješten u smjer osi x i nategnut u tom smjeru, tako da su prve tri komponente deformacije xx, yy=zz=—μxx, a prve tri komponente napetosti Xx, Yy=Zz=0. Ako te veličine uvrstimo u prve dvie jednačbe (15) i uvedemo Youngov modul E s pomoću relacije —Xx = E xx, izlazi s obzirom na (6), da je a—b = 2G i
b = 2μG : (1—2μ). (16)
Ako se veličine, dane Hookeovim zakonom izotropnog tiela (15) Xx, Yy,∙∙∙∙, uvrste u dinamičke jednačbe (10), dobiju se te jednačbe u obliku
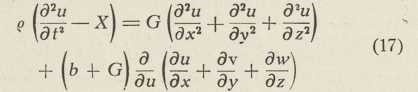
i dvie slične jednačbe za v i za w.
Te je jednačbe odkrio Navier, i to već 1821, kada još nije bio objašnjen obći pojam napetosti. Navierov za elastomehaniku pionirski rad osnivao se na zamisli boškovićanskog elastičnog tiela. Njegove formule razlikuju se od (17) samo time, što je u njima b = G, dakle jedna nezavisna elastična konstanta umjesto dvie. S obzirom na (16) izašlo bi iz toga μ = ¼ (Poissonova tvrdnja).
Za pamćenje Navierovih formula zgodan je njihov vektorski oblik. Ako se pomak čestice (s komponentama u, v, w) vektorski označi sa S, a sila (s komponentama X, Y, Z) sa U, tri se Navierove jednačbe stapaju u jednu, vektorsku:
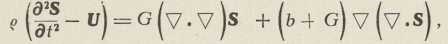
gdje je točka znak skalarne množitbe.
Navierove jednačbe vriede za točke u unutarnjosti elastičnog tiela. Pri rješavanju zadaća jednako su važni uvjeti, kojima je podložena površina tiela.
12. Poobćeni Hookeov zakon, II. Između izotropnih tjelesa, za koje obći Hookeov zakon sadržava samo 2 među sobom nezavisne konstante, i slučaja, gdje takvih konstanata ima 21, kako je to kod ledaca triklinskog sustava, dolaze primjeri sa srednjim brojem konstanata, i to kod ledaca s manje ili više unutarnje simetrije. Tako broj nezavisnih konstanata kod monoklinskih ledaca jest 13, kod rombskih 9, a kod teseralnih samo 3. Ako se koordinatne osi smjeste u smjer kristalografskih, onda za te posljednje ledce vriedi
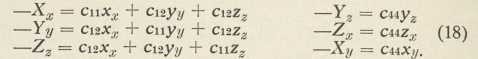
Obći Hookeov zakon nastojali su francuzki teoretičari prve polovine prošloga stoljeća (Cauchy, Poisson, Lamé) izvesti iz hipoteze boškovićanskog elastičnog tiela, dakle iz pomisli, da se tielo sastoji od atoma, koji su tvarne točke i djeluju jedni na druge centralnim silama. Međutim to ih je vazda vodilo na takav Hookeov zakon, u kojemu je broj konstanata bio manji, i to kod izotropnih tjelesa 1 umjesto 2, kod najobćenijih 15 umjesto 21. »Glasovite« t. zv. Cauchyjeve relacije (de Saint-Venant), koje su stezale broj konstanata, bile su c44 = c23, c55 = c31, c66 = c12; cl4 = c56, c25 = c64, c36 = c45.
Međutim je u Englezkoj Green 1837, polazeći od zahtjeva, da postoji t. zv. elastični potencial, tvrdio, da uobće ima 21 nezavisna konstanta. To je termodinamskim putem dokazao i W. Thomson (Lord Kelvin) 1855 za dva važna slučaja: jedan, kada se tielo izobličuje bez promjene temperature, i drugi, kada kod deformacije nema prelaženja topline. Nesklad »multikonstantne« teorije (21 do 2 konstante) i »rarikonstantne« (15 do 1 konstanta) zadugo je ostao neobjašnjen. Pristaše atomistike kušali su različnim putovima doći do većeg broja konstanata. Tako je Poisson umjesto atoma-točaka uveo atome, koji su »kruta tjelešca poliedričkog oblika« te ne djeluju samo centralnim silama jedni na druge, već i parovima sila. Bolje je uspio Voigt, koji dolazi na multikonstantni zakon, zamišljajući molekule »obdarene polarnošću«. Ali pravu misao uvodi tekar Kelvin 1890, koji, stojeći pod dojmom tada još hipotetične kristalografske nauke o poređaju atoma, izpituje dinamiku elastičnog tiela sazdanog iz dva sustava poredanih atoma, koji se sustavi među sobom prodiru. Po Kelvinu »doista najjednostavnija boškovićanska zamisao ledca jest jednoličan skup pojedinačnih točaka; sliedeći po jednostavnosti jest skup dvostrukih točaka«. Na tom osnovu Kelvin doista dobiva 21 konstantu. I kada je Laueovim odkrićem prirode rentgenskih zraka potvrđena atomistička nauka o ledcima, potanko je Kelvinovu misao razradio M. Born (1915), te je time multikonstantna teorija stekla i uvjerljiv atomistički osnov.
Da među komponentama napetosti i komponentama deformacije postoje jednačbe prvoga stupnja, izlazi, na što je Stokes 1845 upozorio, iz jednostavne akustične činjenice, da se visina tona, što ga daje kruto tielo, ne mienja, kada ton postaje slabiji. Obsežna i svestrana mjerenja u svezi s Hookeovim zakonom izveo je G. Wertheim 1842 i dalje. Eksperimentalnu potvrdu za multikonstantnu teoriju zahvaljujemo W. Voigtu, koji je odredio elastične konstante za znatan broj ledaca. Ti s obzirom na zamršenost zadaće — kako Love kaže — smioni pokusi dali su na pr. za pirit (1888), kojega ledci idu u teseralni sustav, te imaju tri različite elastične konstante,
c11 = 36800 kg*/mm2, c12, = —4830, c44 = 10750,
u opreci sa Cauchyjevom rarikonstantnom relacijom c44 = c23 (= c12). Trebalo je odvažiti se na mjerenje elastičnosti ledaca, građe teoretski zamršenije, jer se kod njih može čistoća i jednoličnost lakše izpitati nego kod izotropnih tvari, koje pogledom na homogenost dopuštaju sumnje i prigovore.
LIT.: A. E. H. Love, A Treatise of the Mathematical Theory of Elasticity, Cambridge I. 1892, II. 1893, 2. izd. 1906 (njemački Leipzig 1907); I. Todhunter i K. Pearson, A History of the Theory of Elasticity and of the Strength of Materials, Cambridge I 1886, II1, II2 1893; Lord Kelvin, Baltimore Lectures on Molecular Dynamics and the Wave Theory of Light, London 1904 (njemački Leipzig 1909); Encyklopädie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen IV4, Leipzig 1907—1914 (Čl. 23.—26., 31.); ib. V3 Leipzig 1909—1926 (Čl. 25., napisao M. Born 1923); M. Planck, Einführung in die Mechanik deformierbarer Körper, Leipzig 1919, 3. izd. 1931; S. Timoshenko, Theory of Elasticity, London — New-York 1934 (ruski Leningrad-Moskva 1937); HN (Hrvatske norme) 41, 1943; 42, 1944.St. H.