DIFERENCIJALNA GEOMETRIJA. To je grana geometrije, koja proučava kontinuirane geometrijske tvorevine (krivulje, plohe, prostore) samo u okolišu jedne njihove točke, t. j. u toj točki i onom dijelu tvorevine, koji se nalazi neposredno uz tu točku. Njoj je oprečna ona grana geometrije, koja istražuje spomenute tvorevine u njihovoj cjelini ili totalitetu. Jedna i druga od ove dvije geometrije može se obrađivati na dva načina: sintetički ili analitički; onaj prvi je čisto geometrijski, dok se drugi služi matematičkom analizom (grubo rečeno: računom). U analitičkom načinu razlikujemo pak one dvije geometrije po tome, što se prva služi diferencijalnim (i nešto integralnim) računom (odatle joj i ime), a druga pretežno metodama algebre, pak zato ostaje u granicama analitičke geometrije u užem smislu, ograničujući se na istraživanja t. zv. algebarskih krivulja i ploha; zbog toga se onda zove algebarskom geometrijom. Međutim ima izvjesnih svojstava, koja imaju diferencijalni karakter, makar dotične tvorevine promatrali kao cjelinu (na pr.: broj tjemena nekog ovala; svojstvo kugline plohe, da se ne da deformirati); to je diferencijalna geometrija u velikom. Često se diferencijalna geometrija javlja kao primjena diferencijalnog računa na geometriju, no to zapravo nije diferencijalna geometrija, jer tada geometrija služi samo za ilustraciju pravila i operacija diferencijalnog računa, dok u diferencijalnoj geometriji moraju biti geometrijski pojmovi, svojstva, odnošaji i stavci ono primarno, a diferencijalni račun samo sredstvo za njihovo istraživanje.
Po predmetu, koji istražuje, dijeli se diferencijalna geometrija u difer. geometriju krivulja (ili teoriju krivulja), difer. geometriju ploha (teorija ploha) i difer. geometriju (općenih, n-dimenzionalnih) prostora; s obzirom pak na prirodu operacionog prostora, u kojem zamišljamo »uronjene« te objekte, imamo metričku, afinu i projektivnu difer. geometriju. Metrička je sve do početka ovoga stoljeća bila sama, te se zove i klasičnom difer. geometrijom.
 Sl. 1.
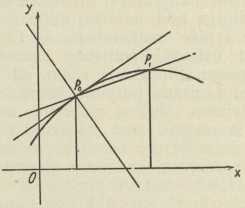
Sl. 1.1. Metrička diferencijalna geometrija: Teorija krivulja. — Tu moramo razlikovati teoriju ravnih krivulja (t. j. krivulja u ravnini) i teoriju prostornih krivulja. Ravnu krivulju možemo analitički predočiti na tri načina: eksplicitno jednadžbom y = f(x), implicitno jednadžbom F(x,y) = o ili parametrički jednadžbama x = φ(t), y = ψ(t) za variabli parametar t; pri tom pretpostavljamo, da su sve ove funkcije monogene, dakle jednoznačne i neprekidne s derivacijama svih potrebnih redova, a za koordinate x, y uzimamo, da su pravokutne. Prvi je problem, koji se tu javlja, pitanje tangente krivulje u njezinoj točki P0(x0,y0); ona nastaje iz sekante P0P1 s pomoću graničnog prijelaza P1→P0, t. j. za slučaj, kada točka P1 po krivulji neograničeno teži prema čvrstoj točki P0 (Sl. 1). Ako tu operaciju provedemo analitički, dobivamo za tangentu po redu ova analitička predočenja:
y—y0 = y0'∙(x—x0),
(x — x0) ∙ Fx0 + (y — y0) ∙ Fy0 = 0, odnosno
x−φ(t0)/φ'(t0) = y−ψ(t0)/ψ'(t0),
gdje su svuda x, y koordinate kurentne točke na tangenti. Za normalu krivulje u točki P0, t. j. pravac, koji ide diralištem P0 okomito na tangentu (Sl. 1), izvode se odatle jednadžbe prema pravilima obične analitičke geometrije.
Drugo je pitanje kod ravnih krivulja problem oskulacione kružnice, t. j. kružnice, koja u točki P(x,y) krivulje ima s ovom tri konsekutivne točke zajedničke (t. j. tri točke, koje slijede jedna »tik« iza druge). Središte (a, b) i polumjer r te kružnice dani su za eksplicitni i parametrički oblik formulama 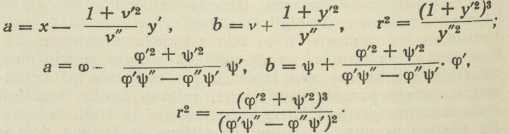 .
.
To se dobiva opet s pomoću graničnog prijelaza na taj način, da postavimo jednadžbu kružnice kroz točku P i bilo koje dvije točke P1, P2 krivulje, pak pustimo, da točke P1 i P2 nezavisno jedna o drugoj po krivulji neograničeno teže prema čvrstoj točki P. Vrlo se lako uviđa i geometrijski i analitički, da središte oskulacione kružnice leži na pripadnoj normali krivulje. Ovo je samo specijalni slučaj općenog problema diranja dviju krivulja (oskulacione parabole i elipse).
 Sl. 2.
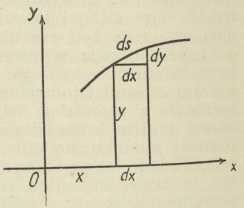
Sl. 2.Luk krivulje je dio krivulje, omeđen dvjema njezinim točkama; duljina luka označuje se sa s, te je dana formulama
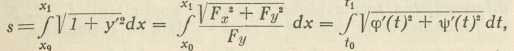
gdje je luk omeđen točkama P0 i P1; te se formule izvedu iz osnovne formule za element luka ili lučni diferencijal (Sl. 2)
ds2 = dx2 + dy2.
Iz zadnjeg oblika za s slijedi, da je za
φ'(t)2 + ψ'(t)2= 1
s=t+C, no konstanta C dade se uvijek učiniti jednakom nuli, ako podesno odaberemo početak računanja duljine luka s, odnosno parametra t; prema tome možemo reći, da u slučaju, kada funkcije φ i ψ zadovoljavaju gornji uvjet, parametar t znači duljinu luka krivulje.
Krivina k krivulje u njezinoj točki P definira se kao granična vrijednost omjera kuta tangenata u točki P i nekoj blizoj točki P1 prema duljini luka 1, kada točka P1 neograničeno teži po krivulji prema čvrstoj točki P; kraće: krivina k je omjer kuta kontingence dτ i elementa luka ds u točki P, gdje se pod kutom kontingence razumijeva kut dviju konsekutivnih tangenata; imamo, dakle, definicionu formulu
k = dτ/ds
Ako tu veličinu dτ razvijemo analitički iz njezinog geometrijskog pojma, dobivamo, da je 1/r, gdje je r polumjer oskulacione kružnice. Zato se oskulaciona kružnica zove još i kružnicom krivine, a njezin polumjer polumjerom krivine. Međutim, kružnicu krivine možemo definirati i posve nezavisno o oskulacionoj kružnici, jer kružnica kao krivulja, koja je posvuda jednako zakrivljena, služi kao model, na kojem se uopće uvodi pojam krivine kao mjere za zakrivljenost (valja dobro lučiti krivinu od zakrivljenosti; ovo je pojam geometrijski, svojstvo krivulje kao takve, dok je krivina broj, koji veli, kolika je zakrivljenost).
 Sl. 3. Sl. 4
Sl. 3. Sl. 4Singularne točke krivulje jesu one, gdje se tangenta, odnosno duljina luka ne vlada kao obično, na pr. ako je za parametrički oblik istodobno φ'(t) = 0, ψ'(t) = 0, tada je tangenta u točki P(t) neizvjesna, element luka jednak nuli, a točka P singularna, i to šiljak (Sl. 3b). Implicitni oblik daje nam tako tri vrsti singulariteta: uzao, šiljak i izoliranu točku (Sl. 3); ova posljednja je točka, koja pripada krivulji, ali nema realne sveze s ostalim točkama krivulje. Eksplicitni pak oblik vodi prirodno do t. zv. točke infleksije, t. j. takve točke na krivulji, koja sa svoje dvije konsekutivne leži na jednom istom pravcu, naime na infleksionoj tangenti te točke (Sl. 4). To su samo najobičniji singulariteti, prema kojima stoje viši singulariteti ravnih krivulja (na pr. šiljak 2. vrsti, samodiranje i t. d.).
Zatim dolazi pitanje asimptota (v.) ravnih krivulja, t. j. tangenata u neizmjerno dalekim točkama tih krivulja; onda teorija anvelopa ili umotaljaka skupa ravnih krivulja: jednadžba F(x,y;a) = 0 znači za variabli parametar a skup od ∞1 krivulja u ravnini, pak se krivulja, koja dira istodobno sve krivulje toga skupa, zove anvelopa ili umotaljka toga skupa. Jednadžba anvelope dobiva se tako, da se iz zadane jednadžbe skupa i jednadžbe ∂F(x, y;a)/∂a= 0 eliminira parametar a.
Ako tu teoriju anvelopa primijenimo na skup normala neke ravne krivulje, dobivamo t. zv. evolutu te krivulje kao anvelopu njezinih normala; za nju se može smjesta konstatirati, da je identična s geometrijskim mjestom središta oskulacionih kružnica zadane krivulje. Na pojam evolute nadovezuje se odmah pojam evolvenata; to su krivulje, za koje je zadana krivulja evoluta; svaka ravna krivulja ima samo jednu evolutu, ali ∞l evolvenata. Sve je to samo kratki sumarni prikaz sadržaja diferencijalne geometrije ravnih krivulja, a potankosti treba pogledati u dolje navedenoj literaturi.
2. — Prostorna krivulja je ona, koja se ne može smjestiti u jednu ravninu ili u više njih. Glavna poglavlja teorije prostornih krivulja jesu: tangenta, normale i normalna ravnina; oskulaciona ravnina; trobrid pratilac s glavnom normalom i binormalom te rektifikacionom ravninom; diranje dviju krivulja, odnosno krivulje i plohe, te specijalno oskulaciona kružnica i kugla s polarnom osi; popratne plohe prostorne krivulje: tangentna ploha, polarna ploha i rektifikaciona developabla, te ploha glavnih normala, odnosno binormalâ; duljina luka i singularne točke; fleksija i torzija sa sfernim preslikavanjem prostorne krivulje; asimptote; evolute i evolvente (jedne i druge filarne, odnosno planarne) i t. d.
Analitički je prostorna krivulja predočena opet eksplicitno jednadžbama y — f(x), z = g(x) ili implicitno jednadžbama F(x,y,z) = 0, G(x,y,z) = 0 ili parametrički x — φ(t), y =φ(t), z = χ(t), gdje je t neki variabli parametar; sve su funkcije monogene, a koordinatni sustav je pravokutan. U prvom je slučaju krivulja presjek dviju cilindričnih, a u drugom dviju općenih ploha. Tangenta u točki P(t) u trećem je slučaju dana jednadžbama
x−φ(t)/φ'(t) = y−ψ(t)/ψ'(t) = z−χ(t)/χ'(t)
dakle ima normalna ravnina, t. j. ravnina okomita na tangentu u njezinom diralištu, jednadžbu
[x — φ(t)] ∙ φ'(t) + [y—φ(t)] ∙ φ'(t) + [z — χ(t)] ∙ χ'(t) = 0.
Tu su svuda x, y, z koordinate kurentne točke tangente, odnosno normalne ravnine. Oskulaciona ravnina, t. j. ravnina, koja ide trima konsekutivnim točkama P, P1, P2 krivulje, ima jednadžbu 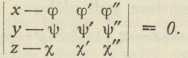
 Sl. 5.
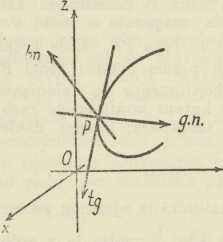
Sl. 5.Presječnica normalne i oskulacione ravnine u točki P je glavna normala krivulje u toj točki, a okomica, dignuta u P na oskulacionu ravninu, zove se binormala, jer je okomita i na tangentu i na glavnu normalu; ravnina tangente i binormale zove se rektifikaciona ravnina prostorne krivulje u dotičnoj točki. Tri pravca: tangenta, glavna normala i binormala u točki P krivulje čine tropravokutni trobrid, koji se zove trobrid pratilac krivulje u točki P (Sl. 5); njegove su strane oskulaciona, normalna i rektifikaciona ravnina. Jednoznačno je određen tangentom i oskulacionom ravninom, te se mijenja od točke do točke krivulje, dakle zajedno s parametrom t.
Element luka ds prostorne krivulje dan je formulom
ds2 = dx2 + dy2 + dz2 = [φ'(t)2 + φ'(t)2 + χ'(t)2] dt2,
pa u slučaju
φ'(t)2 + φ'(t)2 + χ(t)2 = 1
opet parametar t znači duljinu luka s. To je važno zbog toga, što se tada sve daljnje istraživanje prostornih krivulja izvanredno pojednostavnjuje. Uzimamo dakle, da je prostorna krivulja od sada zadana ovako
x = φ(s), y = φ(s), z = χ(s).
Tada su kosinusi smjera (t. j. kosinusi kutova, što ih dotični pravac čini s pozitivnim smislovima koordinatnih osi) α, β, γ tangente, l, m, n, glavne normale, te λ, μ, ν binormale dani formulama
a = x' , l = rx" , λ = r (y'z" — y"z') ,
β = y' , m = ry" , μ = r (z'x" — z"x') ,
γ = z' ; n = rz" ;ν = r x'y" — x"y') ,
gdje se derivacije imaju uzeti po parametru s, a r znači polumjer prve krivine ili fleksije prostorne krivulje, dan formulom
1/r = dT/ds = √ x''2 + y''2 + z''2 ;
tu je dT kut kontingence. Za čitavu teoriju prostornih krivulja fundamentalne su Frenet-Serretove formule
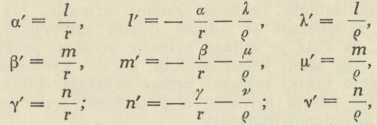
gdje opet crtica znači deriviranje po parametru s, a ϱ je druga krivina ili torzija prostorne krivulje, dana formulom

tu je dB t. zv. kut torzije, t. j. kut dviju konsekutivnih binormala.
Čitava daljnja teorija prostornih krivulja izvodi se s pomoću tih formula i s pomoću tračnih specijalno developablih ili razvojnih ploha. Važna je pri tom ova činjenica: teorija prostornih krivulja ne da se potpuno razviti bez pojma plohe; to je jedna neskladnost u diferencijalnoj geometriji, jer to suponira, da već znamo teoriju ploha prije teorije krivulja. Međutim, tu se radi samo o jednoj specijalnoj vrsti ploha, kojih se nama potrebna svojstva daju vrlo lako razviti i bez općene teorije ploha, a s druge strane, developable plohe zapravo su prostorni dualistikum samih prostornih krivulja.
 Sl. 6.
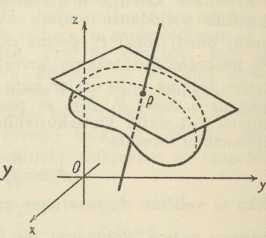
Sl. 6.3. Teorija ploha. Analitički se ploha predočuje opet eksplicitno: z = f(x, y), implicitno: F(x, y, z) = 0 ili parametrički (Gauss): x=φ(u, v), y=ψ(u, v), z=χ(u, v), gdje su u, v među sobom nezavisni variabli parametri; sve funkcije suponiramo i tu kao monogene, a koordinatni sustav kao pravokutan. Za konstantnu vrijednost parametra v znače posljednje tri jednadžbe neku prostornu krivulju na našoj plohi i analogno za konstantnu vrijednost parametra u; to su t. zv. parametarske crte plohe, koje čine parametarsku mrežu na plohi. Sami parametri u i v zovu se krivocrtne koordinate točke P na plohi, jer određuju mjesto te točke na plohi na podlozi one mreže. Prvo je tu pitanje tangencijalna ravnina plohe u njezinoj točki P 0 (Sl. 6); ona ima jednadžbu
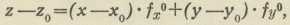
odnosno
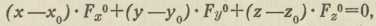
odnosno
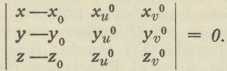
Odatle se lako dobiju jednadžbe normale plohe u točki P0. Čitava daljnja teorija ploha zavisi o izrazu za linijski element plohe; to je element luka bilo koje krivulje, koja izlazi iz točke P(u, v) na plohi. Označuje se opet sa ds, a najzgodniji analitički izraz za nj dobivamo u Gaussovom parametričkom predočenju plohe, u obliku
ds2 = Edu2 + 2 F du dv + G dv2.
Desna je strana t. zv. prva fundamentalna kvadratna diferencijalna forma zadane plohe, a E, F, G su fundamentalne veličine 1. reda; njihovi analitički izrazi dobiju se tako, da se u osnovnu formulu ds2 = dx2 + dy2 + dz2 uvrste izrazi za diferencijale dx, dy, dz dobiveni iz jednačaba same plohe, a glase
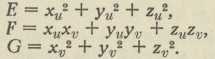
Krivulje na plohi, uzduž kojih je u svakoj točki ds = 0, dane su diferencijalnom jednadžbom
Edu2 + 2Fdudv + Gdv2 = 0,
te se zovu minimalne krivulje plohe; one su uvijek imaginarne.
Dalje se teorija ploha razvija tako, da se plošnom normalom točke P, u okolišu koje istražujemo svojstva plohe, polože različite ravnine; one određuju s plohom t. zv. normalne presjeke, pak je tada polumjer krivine R jednog takvog presjeka dan formulom
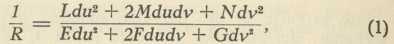
gdje je u brojniku t. zv. druga fundamentalna kvadratna diferencijalna forma plohe, a njezini koeficijenti L, M, N — fundamentalne veličine 2. reda — dani su formulama
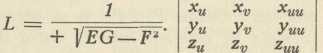
i analogno za M i N s tom promjenom, da mjesto xuu dolazi xuv, odnosno xvv, i isto za y i z. Druga fundamentalna forma važna je zato, jer ona određuje odnošaj plohe prema vanjskom svijetu, t. j. prema operacionom prostoru, u kojem se ploha nalazi (dakle određuje oblik plohe), dok je 1. fundamentalna forma mjerodavna samo za geometriju na samoj plohi. Ako je ploha zadana svojim jednadžbama, tada je time već suodređeno njezinih šest fundamentalnih veličina E, F, G, L, M, N; a fundamentalni problem teorije ploha sadržan je u obrnutom pitanju: da li šest po volji zadanih funkcija dvaju parametara u, v znače u svakom slučaju fundamentalne veličine neke plohe. Odgovor je dao O. Bonnet g. 1867.: To će biti onda i samo onda, ako te funkcije zadovoljavaju izvjesne tri t. zv. fundamentalne jednadžbe plohe i ako je EG — F2 ≠0. To je t. zv. teorem o eksistenciji i unitetu plohe.
Iz formule (1) izvode se sada glavni normalni prosjeci, t. j. ona dva, za koja R ima maksimalnu, odnosno minimalnu vrijednost; te se dvije vrijednosti označuju sa R1, R2 i zovu polumjeri glavnih krivina. Dalje se iz toga izvode crte krivine, predočene diferencijalnom jednadžbom
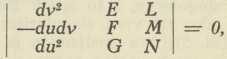
zatim Eulerova jednadžba
1/R = cos2φ/R1 + sin2φ/R2
gdje je φ kut, što ga normalni presjek (R) čini s glavnim normalnim prosjekom (R1); nadalje Dupinova indikatrisa, onda asimptotski smjerovi na plohi u njezinoj točki P i s tim u svezi u jednu ruku tri vrste točaka plohe (eliptične, hiperboličke i paraboličke), a u drugu asimptotske crte na plohi predočene diferencijalnom jednadžbom
Ldu2 + 2Mdudv + Ndv2 = 0.
Posebno stoji pitanje geodetskih crta na plohi; to su krivulje najkraće udaljenosti dviju točaka na plohi, te se njihova diferencijalna jednadžba dobiva iz tog pojma s pomoću metoda računa variacijâ; no nasuprot tog integralnog svojstva tih crta stoji direfencijalno svojstvo, da je njihova glavna normala u svakoj točki identična s plošnom normalom. Primjer: u ravnini su geodetske crte pravci, na kuglinoj plohi najveće ili glavne kružnice, na rotacionoj cilindričnoj plohi spirale. Za analitičko obrađivanje geodetskih crta dobro nam služe t. zv. Christoffelovi simboli.
Posebno poglavlje teorije ploha otvara pojam totalne ili Gaussove krivine plohe u nekoj njezinoj točki P; definira se i njezin analitički izraz izvodi s pomoću t. zv. sfernog preslikavanja plohe, t. j. preslikavanja te plohe na jediničnu kuglu po izvjesnom propisu. Na to se nadovezuju poglavlja o deformaciji ploha (t. j. pregibanju ili previjanju ploha bez trganja i nabiranja, zatim o preslikavanju plohe na plohu (konformno, ekvilongno, ekviarealno; važno za kartografiju), namatanje plohe na plohu i t. d.
Od daljnjih poglavlja diferencijalne geometrije ploha neka budu spomenuta ova: općena teorija krivulja na plohi i njihovih mreža (izotermičke, geodetske i t. d.), geodetska krivina (Bonnet), diferencijalni parametri (Beltrami), paralelni pomak uzduž neke crte na plohi (Levi-Civita) i t. d.
Od posebnih familija ploha važne su ove: tračne ili pravčaste, specijalno razvojne ili developable; rotacione; anvelope plohâ; translatorne plohe; kanalne plohe (Monge); Weingartenove ili W-plohe; minimalne plohe (plohe najmanje površine unutar zadane konture; za njih je srednja krivina H = 1/R1 + 1/R2 jednaka nuli), te plohe konstantne krivine. Ove posljednje osobito su važne zbog toga, što se daju pomicati u sebi bez trganja i nabiranja i što se na njima dadu euklidski interpretirati neeuklidske planimetrije (hiperbolička ili Lobačevskoga na t. zv. pseudosferi, sferno-eliptična ili Riemannova na običnoj kuglinoj plohi, odnosno polukugli, a parabolička ili euklidska na bilo kojoj developabloj plohi).
4. Teorija prostorâ. Ako sa Rn i Sn označimo neki n-dimenzionalni ravni, odnosno zakrivljeni prostor, tada nam R0 i S0 znače točku, R1 i S1 pravac, odnosno krivulju, R2 i S2 ravninu, odnosno zakrivljenu plohu, a onda analogno R3 i S3 znače ravni, odnosno zakrivljeni trodimenzionalni prostor i t. d. Od tih tvorevina možemo realizirati sve do uključivo R3, dok za S3, R4, S4,... više nemamo zorne predodžbe. Ali možemo S3 analitički obrađivati tako, da ga zamislimo uronjenog u neki ravni operacioni prostor sa više od tri dimenzije, recimo u R4: u tu svrhu uzimamo, da u tom R4 postoji neki pravokutni kartezijev koordinatni sustav s ishodištem O i koordinatnim osima OX1, OX2, OX3, OX4 te koordinatama x1, x2, x3, x4. To je, dakako, puka generalizacija onoga, što smo imali u R3 za S0, S1 i S2, bez ikakve geometrijske podloge; od geometrije je uzeta samo terminologija. Općeno se tako mogu u operacionom prostoru Rn proučavati tvorevine S0, S1, S2,..., Sn-1, t. j. točke, krivulje, plohe, te prostori svih dimenzija do uključivo n — 1; svi se ovi Sr za 0r < n zovu podprostori operacionog prostora Rn, a Sn-1 napose hiperplohe od Rn. Dakako, da su tu uključeni specijalno i ravni podprostori, t. j. pravac, ravnina i t. d. te napokon hiperravnina Rn-1. Analitički aparat za istraživanje tih tvorevina dobiva se na podlozi koordinatnog sustava Ox1x2... xn.
Krivulje S1 su na pr. sada predočene jednadžbama
x1 = φ1(t), x2 = φ2 (t),..., xn = φn(t), gdje je
t variabli parametar, a φ1, φ2,..., φn izvjesne zadane monogene funkcije od t; hiperploha Sn-1 pak ima jednadžbe
x1 = φ1(u1, u2,..., un-1), x2 = φ2(u1,u2,..., un-1),
...., xn = φn (u1, u2,..., un-1),
gdje su u1, u2,..., un-1 među sobom nezavisni variabli parametri.
Kada smo od S1 u R2 prešli na S1 u R3, t. j. od ravnih krivulja na prostorne, vidjeli smo, da je opseg teorije prostornih krivulja bio znatno veći od onoga kod ravnih krivulja; pogotovo pak to vrijedi, kada od S1 u R3 prijeđemo na S2 u R3, t. j. od prostornih krivulja na plohe u našem običnom prostoru. Zato je bez daljnjega jasno, da će kod svakog daljnjeg koraka opseg svojstava novih tvorevina ubrzano rasti, te će na pr. u općenom slučaju, t. j. kada proučavamo bilo koji podprostor Sr u Rn, teorija već biti vrlo opsežna. Ta se istraživanja nalaze izvanredno lijepo prikazana u djelima D. J. Struik, Grundzüge der mehrdimensionalen Differentialgeometrie, Rotterdam 1922, J. A. Schooten, Der Ricci-Kalkül, Berlin 1923, te Schooten-Struik, Einführung in die neueren Methoden der Differentialgeometrie, 2 sv., 2. izd., Groningen 1938. Istaknut ćemo ovdje još samo to, da kao analitički instrument za ta istraživanja služi isključivo t. zv. apsolutni diferencijalni račun, kojega je god. 1887 stvorio G. Ricci, a koji je dugo ostao neopažen i neupotrebljen.
5. Afina i projektivna diferencijalna geometrija proučavaju ona svojstva geometrijskih tvorevina Sr u opera
cionom prostoru Rn, koja ostaju invarijantna s obzirom na grupu ekviafinih, odnosno projektivnih transformacija (grupa općenitih afiniteta u tom je pogledu manje važna). Da navedemo samo nekoje osnovne pojmove tih dviju difer. geometrija: afina resp. projektivna duljina luka, afina resp. projektivna krivina i t. d.; od pojmova, poznatih već iz metričke diferencijalne geometrije, spadaju u projektivnu difer. geometriju na pr. konjugirane tangente i asimptotske crte. Začetnik je afine difer. geometrije G. Pick (Affine Flächentheorie, Prag 1916), a među nastavljačima je najvažniji W. Blaschke (Vorlesungen über Differentialgeometrie, 2. sv., Berlin 1923); projektivnu difer. geometriju osnovao je E. J. Wilczynski (Projective differential geometry, Leipzig 1906), dok je danas najbolje djelo o toj geometriji G. Fubini i E. Čech, Geometria proiettiva differenziale, 2 sv., Bologna 1926/27.
6. Historijat. Diferencijalna geometrija ravnih krivulja nerazdruživo je povezana s postankom i razvitkom diferencijalnog i integralnog računa. Prva istraživanja iz difer. geometrije prostornih krivulja ploha jesu ona, koja je proveo I. Bernoulli 1697 o geodetskim crtama na plohi. Iza toga su dali važne priloge o prostornim krivuljama Clairaut 1731, Tinseau 1780, Euler 1782, Monge 1795, Lancret 1806 i de Saint-Venant 1845. Od Clairauta potječe naziv krivulje dvostruke krivine za prostorne krivulje; Tinseau je prvi promatrao oskulacionu ravninu; Euler je uveo duljinu luka kao parametar i dao gore navedenu formulu za polumjer fleksije; Monge je dao jednadžbu normalne ravnine, te otkrio polarnu plohu i planarne evolute prostorne krivulje; Lancret je uveo pojam kuta kontingence i kuta torzije pod nazivom prva i druga fleksija, te je prvi izračunao torziju prostorne krivulje, od njega potječe i pojam rektifikacione ravnine, te je proučavao rektifikacionu developablu i odredio jednadžbe filarnih evoluta; de Saint-Venant je uveo pojam binormale i dao jednostavne formule za elemente oskulacione kugle. Frenet-Serretove formule našli su Frenet god. 1847, a Serret ponovno 1851. Naziv trobrid pratilac uveo je Schell g. 1859 u djelu Allgemeine Theorie der Kurven doppelter Krümmung, 3. izd., Leipzig-Berlin 1914, koje je važno zbog toga, što proučava diferencijalna svojstva prostornih krivulja čisto geometrijski.
I difer. geometrija ploha dobiva čvrste temelje u drugoj polovici 18. st. Euler istražuje g. 1767 polumjere krivina normalnih presjeka plohe, te određuje najveći i najmanji među njima, a 1771 proučava plohu tangenata prostorne krivulje; Tinseau i Monge daju istodobno g. 1780 jednadžbu tangencijalne ravnine, a Meusnier dopunjuje g. 1785 Eulerova istraživanja o normalnim presjecima. Međutim, temeljna dva djela za općenu teoriju ploha jesu: Monge, Feuilles d’analyse appliquée à la géométrie, Pariz 1795, od 3. izdanja (1807) pod naslovom Application de l’analyse à la géométrie, te Gauss, Disquisitiones generales circa superficies curvas, Göttingen 1828. Monge uvodi pojam familije ploha, definiranih s pomoću neke parcijalne diferencijalne jednadžbe (cilindrične, stožaste, rotacione i kanalne plohe, konoidi, plohe najjačeg priklona, tračne plohe), zatim pojam karakteristika kod anvelope ploha; otkriva crte krivine i evolutnu plohu za zadanu plohu. Od učenika Mongeovih Dupin je u djelu Développement de géométrie, Pariz 1813, uveo glavne tangente, konjugirane tangente i indikatrisu, te je dao stavak o crtama krivine kod trostruko ortogonalnih sustava ploha; g. 1822 pak istražuje plohe ciklide, koje se danas nazivaju njegovim imenom. Ali nadasve je važno Gaussovo djelo, jer je u njemu Gauss uveo predočenje plohe s pomoću dva parametra, a to je bilo odlučno za daljnji razvoj teorije ploha, budući da time sve formule dobivaju izvanredno prikladan i simetričan oblik. U stvarnom pogledu donosi to djelo važan princip sfernoga preslikavanja, zatim definiciju i formulu za krivinu plohe u nekoj njezinoj točki (to je ujedno jedna od tri gore spomenute fundametalne jednadžbe plohe, dok su ostale dvije dali Mainardi 1856 i Codazzi 1860), te primjenu toga pojma na deformaciju ploha, namatanje jedne plohe na drugu (theorema egregium) i na koncu svojstva geodetskih crta. Daljnji važni momenti u razvoju teorije ploha spomenuti su već gore u odsječku 4.
Poslije intenzivnoga rada mnogih geometara dao je potkraj 19. stoljeća G. Darboux u svom kapitalnom djelu Leçons sur la théorie générale des surfaces, 4 sv., Pariz 1887, 1889, 1894, 1896, sintezu svega tadašnjega znanja o općenitim svojstvima ploha. Isti značaj ima i djelo L. Bianchi, Lezioni di geometria differenziale, 2 sv., Pisa 1885/86, 3. izd., 2 sv. po 2 dijela, Bologna-Pisa 1927, 1927, 1923, 1924.
LIT.: Osim gore navedenih djela još ova: F. Joachimsthal, Anwendung der Differential- und Integralrechnung auf die allgemeine Theorie der Flächen und der Linien doppelter Krümmung, Leipzig 1872, 3. izd. 1890; E. Cesàro, Vorlesungen über natürliche Geometrie, sa tal. preveo G. Kowalewski, Leipzig 1901; J. Knoblauch, Grundlagen der Differentialgeometrie, Leipzig-Berlin 1913; G. Scheffers, Anwendung der Differential-und Integralrechnung auf Geometrie, 2 sv., 3. izd., Berlin-Leipzig 1923, 1922; A. Duschek i W. Mayer, Lehrbuch der Differentialgeometrie, 2 sv., Leipzig-Berlin 1930; V. i K. Kommerell, Theorie der Raumkurven und krummen Flächen, 4. izd., 2 sv., Berlin-Leipzig 1931; E. Salkowski, Affine Differentialgeometrie, Berlin-Leipzig 1934; R. Sauer, Projektive Liniengeometrie, Berlin-Leipzig 1937.R. C.