DETERMINANTA (ili odreditelj) 1. u matematici je jedna vrst polinoma, koja se javlja u različnim granama matematike, posebno kod rješavanja sustava linearnih algebarskih jednadžba. Na pr., imamo li jednadžbe (1) ax + by = c, a' x + b' y = c', to množeći prvu sa b', a drugu sa — b i zbrojivši ih, dobijemo (a b' — a' b) x = b' c — b c'; slično (a b' — a' b) y = a c' — a' c. Tu dakle imaju nepoznanice x, y isti koeficijent a b' — a' b, koji se zove determinanta sustava (1) i označuje se simbolički sa |aa bb| t. j. taj je simbol kratica za binom a b' — a' b.
Tako imamo:
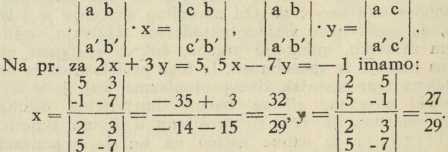
Slično ćemo za sustav od 3 linearne jednadžbe sa 3 nepoznanice
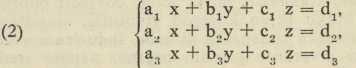
imati: D ∙ x = D1 D ∙ y = D2, D ∙ z = D3, gdje D znači determinantu sustava (2) t. j. šestoročlan a1 b2 c3, — a1 b3 c2 — a2 b1 c3, + a2 b3 c1 + a3 b1 c2 — a3 b2 c1, koji se još označuje sa
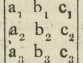 ; D1 znači determinantu, koja se iz D dobije tako, da se u njoj prvi stupac zamijeni s desnom stranom d1, d2, d3 sustava (2); slično D2 i D3; na pr. D3 =
; D1 znači determinantu, koja se iz D dobije tako, da se u njoj prvi stupac zamijeni s desnom stranom d1, d2, d3 sustava (2); slično D2 i D3; na pr. D3 = 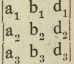
2. Sheme s dva indeksa. Matrice. Kao što se članovi jednostavnog niza mogu označiti s pomoću indeksa, na pr. a, a, a,... tako da na pr. a3 znači treći član niza, tako se i članovi neke kvadratne sheme, recimo ove:
mogu označiti s dva indeksa, od kojih prvi znači redak, a drugi stupac sheme, u kojima se dotični elemenat nalazi; na pr. elemenat 1 gornje sheme nalazi se u 1. retku i 2. stupcu, pa se zato može označiti sa a12; slično 5 = a11,
— 2 = a21, 7 = a22 i prema tome shema glasi:
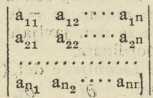
Slično bi se pisale kvadratne sheme ili kvadratne matrice duljine i širine 3, 4,... općeno duljine i širine n, a onda i pravokutne sheme ili matrice bilo kojih dimenzija; tako je na pr.

pravokutna shema duljine s (s stupaca) i širine r (r redaka); opći joj je član aik, (i = 1, 2,.., r; k = 1, 2,..., s). Ispuštanjem pojedinih stupaca ili redaka (ili oboje) u pravokutnoj matrici mogu nastati druge matrice, specijalno kvadratne; tako na pr. iz »proširene matrice« sustava (1):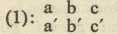
ispuštanjem zadnjeg stupca nastaje kvadratna matrica,iz koje se tvori determinanta sustava (1). Matrice se obično označuju s 4 uspravna poteza, sa svake strane po 2, na pr.
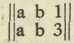 .
.
3. Permutacije. Permutirati zadani niz elemenata na pr. a, b, c znači napisati te elemente u nekom drugom redosljedu, na pr. b, a, c ili c, a, b i t. d.; tako elementi 1, 2 daju samo dvije permutacije: 1, 2 i 2, 1; elementi 1, 2, 3, daju 1 ∙ 2 ∙ 3 = 3! = 6 permutacija i to:
1 2 3, 2 1 3, 3 1 2,
1 3 2; 2 3 1; 3 2 1.
Slično brojevi 1,2,3,.., n daju 1∙2∙3... n = n! permutacija.
Svaki put, kad se u kojoj permutaciji brojeva 1,2,3,.., n nalazi veći broj ispred manjega, kao što je na pr. 3 ili 2 ispred 1 ili 2 ispred 1 u permutaciji 3 2 1, velimo, da permutacija ima inverziju; na pr. 3 2 1 ima tri inverzije. Ako je broj inverzija u permutaciji neparan (paran ili 0), permutacija se zove neparna (parna).
4. Definicija determinante. Da dobijemo izraz za determinantu
postupamo ovako: načipimo »glavni član« a11 a22...ann, t. j. produkt elemenata na dijagonali, što ide s lijeva odozgo (»glavna dijagonala«); zatim se u tom članu mjesto permutacije 1 2 3... n drugih indeksa napiše kojagod permutacija brojeva 1, 2..., n i pred tako dobiven produkt stavi znak + , ako je ona permutacija parna odnosno znak —, ako je neparna; konačno se svi tako dobiveni »članovi« determinante zbroje. Na pr. |a11| = a11 t. j. determinanta reda 1 jednaka je svojem elementu; dalje je  , jer je glavni član a11 a22, a još jedina preostala permutacija drugih indeksa 1, 2 jest 2, 1, pa kako je neparna, daje član —a12 a21 determinante. Dakle: det. 2. reda je jednaka produktu elemenata na glavnoj dijagonali umanjenom za produkt elemenata na sporednoj dijagonali.
, jer je glavni član a11 a22, a još jedina preostala permutacija drugih indeksa 1, 2 jest 2, 1, pa kako je neparna, daje član —a12 a21 determinante. Dakle: det. 2. reda je jednaka produktu elemenata na glavnoj dijagonali umanjenom za produkt elemenata na sporednoj dijagonali.
Slično imamo:
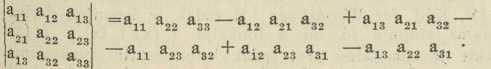
Tako na pr. permutacija 2 3 1 daje član + a12 a23 a31, koji se dobije formalno iz a1 a2 a3 tako, da se tu upišu još drugi indeksi po redu 2, 3, 1 i sprijeda stavi +, jer je permutacija 2 3 1 parna (2 ispred 1, a 3 ispred 1 daje dvije inverzije).
Det. 3. reda može se ovako izračunati: uz zadanu det. s desne strane pripišu se njena prva dva stupca, pak se u tako nastaloj pravokutnoj shemi
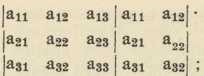
načine produkti elemenata na kosim crtama, te se tim produktima dade znak + ili —, prema tome, da li je dotična kosa crta istoga smjera s glavnom ili sa sporednom dijagonalom determi
nante (Sarrusovo pravilo).
5. Determinante se mogu tumačiti i geometrijski, jer det.

znači sa n! pomnoženi volumen »paralelepipeda« s osnovnim bridovima OV1, OV2,..., OVn, gdje je O ishodište pravokutnog koordinatnog sustava u n-dim. prostoru, a Vi njegova točka (ail, ai2,..., ain), za svaki i = 1, 2,..., n (isp. G. Bouligand, Géométrie vectorielle, Pariz 1924).
6. Nekoja svojstva determinanata. I. Zamijene li se u det. među sobom dvije paralelne crte (dakle 2 redka ili 2 stupca), vrijednost det. mijenja jedino svoj predznak; ako se dakle pritom det. ne mijenja, ona je = O.
II. Ako se u det. D. svaki član nekoga redka ili nekoga stupca pomnoži istim brojem a, dobivena je det. = a. D.
III. Ako su članovi nekog redka (stupca) jednaki ili proporcionalni s članovima kojega drugog redka (stupca), det. je — O.
IV. D. ne mijenja svoje vrijednosti, ako se kojem redku (stupcu) doda koji drugi redak (stupac) pomnožen s bilo kojim brojem.
V. D. ne mijenja svoje vrijednosti, ako se u njoj redci zamijene stupcima, a stupci redcima, t. j. ako se ona preloži po glavnoj diagonali. Ta se operacija zove transponiranje d-e, a dobivena det. transponirana det. od zadane.
VI. Algebarski komplemenat. Laplaceovo pravilo (1772). Precrtamo li u nekoj d-i D redak i stupac, u kojima se nalazi elemenat aik, dobit ćemo opet det., koja se, uzeta s predznakom (—1)i+k zove algebarski komplemenat od āik i označuje sa āik ili još bolje āik (D)
Laplaceovo pravilo glasi:

dakle u prvom slučaju:
ail āil + ai2 āi2 + ... ain āin = D,
t. j. pomnože li se elementi nekoga redka po redu sa svojim algebarskim komplementima, tada je suma tih n produkata jednaka samoj d-i (razvijanje d-e po zadanom redku). Tako je na pr. razvito po 2. redku:
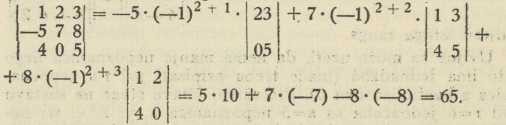
VII. Produkt dviju det. istoga reda opet je det. istog reda, kojoj se elemenat u sjecištu i-tog redka i k-tog stupca dobije kao skalarni produkt i-tog redka prve det. i k-tog stupca druge (Binet, Cauchy 1812).
(Skalarni produkt dvaju nizova brojeva a1 a2,.., an i b1 b2,.., bn je izraz a1 b1 + a2 b2 + ... + an bn, t. j. zbroj produkata korespondentnih brojeva onih dvaju nizova). Tako je na pr.:
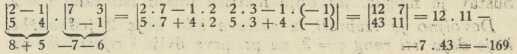
VIII. Ako se svaki član det. D zamijeni svojim algebarskim komplementom, nastaje t. zv. recipročna ili adjungirana det., a vrijednost joj je Dn—1, gdje je n red det. D.
7. Rang determinante i matrice (Frobenius 1887). Velimo, da matrica ima rang ς, ako ona ima bar jednu det. stupnja ς, kojoj je vrijednost ≠ 0, dok su sve det. stupnja ς + 1, izvađene iz te matrice, jednake 0; pri tom se kaže, da je det. izvađena iz matrice ili da je subdeterminanta matrice, ako nastaje ispuštanjem određenog broja stupaca i redaka. Slično se definira i rang det. i to je rang njene matrice.
8. Primjena determinanata na linearne jednadžbe.
I. Cramerovo pravilo (1750). Imamo li sustav od n linearnih jedn. s n nepoznanica x1, x2,..., xn
a11 x1 + a12 x2 + .... + a1n xn = b1,
................................................
anl x1 + an2 x2 + .... ann xn =bn,
tada ćemo — množeći te jednadžbe po redu s alg. kamplementima ā11, ā21, ..., ān1 i zbrojivši ih — dobiti prema Laplaceovom pravilu Ax1 = A1; slično Ax2 = A2,..., Axn = An; pritom je A det. samoga sustava, a A1, A2, ..., An nastaju iz A zamjenjujući u A prvi, drugi, ..., n-ti stupac resp. desnom stranom b1 b2, ... bn sustava.
Homogene jednadžbe. Ako desne strane iščezavaju: b1 = b2 = ... = bn = 0, tada kažemo, da je sustav homogen; homogeni sustav ima sigurno rješenje
x1 = x2 = ... = xn = 0;
a da on ima još koje drugo rješenje, nužno je i dovoljno, da det. sustava iščezava, t. j. da bude A = O.
To se pravilo mnogo upotrebljava kod t. zv. eliminacije n + 1 nepoznanice iz n jednadžbâ. Na pr. nađimo jednadžbu pravca u ravnini kroz dvije točke M/x1, y1), N/x2, y2); ta jednadžba ima sigurno oblik ax+by+c=0, gdje koef. a, b, c nisu istodobno = 0; k tome je ax1 + by1 + c = 0 i ax2 + bx2 + c = 0 kao analički izraz geometrijske činjenice, da točke M, N leže u onom pravcu; imamo dakle 3 homogene jedn. sa 3 nepoznanice a, b, c s rješenjem različitim od samih 0; stoga mora det. sustava biti = 0, t. j.
|
| = 0.
A to je tražena jedn. pravca zadanim dvjema točkama.
II. Opći slučaj sustava linearnih jednadžba. Sustav
a11 x1 + a12 x2 + .... + a1s xs =b1,
a21 x1 + a22 x2 + .... + a2s xs = b2,
...................................................
ar1 x1 + ar2 x2 + .... + ars xs = bs
moguć je onda i samo onda, ako njegova matrica ima isti rang kao t. zv. proširena matrica t. j. matrica, koja se iz matrice sustava dobije pripisujući joj kao (s + l)-ti stupac brojeve b1, b2,.. br; tako na pr. sustav 2x — 3y = 4, 4x — 6y = 2 nije moguć, jer matrice 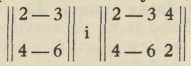 nijesu istoga ranga.
nijesu istoga ranga.
Uvijek se može uzeti, da nema manje nepoznanica nego što ima jednadžba (inače treba pripisati još r-s nepoznanica s koeficijentima 0). Prikažimo čitavu stvar na sustavu od r=6 jednačaba sa s=5 nepoznanica x, y, z, v, w; napišimo taj sustav odmah i šestom nepoznanicom t, koju ćemo, jer nije zadana, staviti u zagrade:
2x — 3y + z — 2v + 5w / + 0.t/ = 5,
4x — 6y — z + v — 3w / + 0.t/ = 0,
—2x + 3y + 5z — 8v + 21w / + 0.t) = 0,
4x — 6y + 5z — 9v + 23w / + 0.t/ = 20,
— 3z + 5v — 13w /+ 0.t/ = —10, 4x — 6y + 2z — 4v + 10w / + 0.t/ = 10.
Sustav je moguć, jer obje matrice imaju isti rang ς = 2.
Dovoljno je izabrati iz sustava bilo koje 2 jednadžbe, koje daju isti rang ς = 2, na pr. prve dvije i riješiti ih; uzmimo prve dvije i napišimo taj t. zv. reducirani sustav tako, da det. u lijevom uglu ne bude = 0 na pr. ovako:
—3y + z + 2x — 2v + 5w + 0.t = 5,
—6y — z + 4x + v — 3w + 0.t = 0.
Opće rješenje toga reduciranog (dakle i zadanog) sustava dobije se pribrajajući jednom njegovom specijalnom rješenju (na pr. rješenju: x = v = w = t = 0, y = — 5, z = 10) opće rješenje homogenog reduciranog sustava
—3y + z + 2x — 2v + 5w + 0.t = 0,
—6y — z + 4x + v — 3w + 0.t = 0.
Po Frobeniusu ovo se rješenje dobije ovako: matricu reduciranoga homogenog sustava treba nadopuniti na kvadratnu matricu pripisivanjem novih s — ς redka, u našem slučaju 4 redka, od kojih se svaki sastoji od samih 0 izuzevelemente, koji padaju na glavnu diagonalu; oni su = 1; u našem dakle slučaju dobijemo ovu matricu:
| —3 |
1 |
2 |
—2 |
5 |
0 |
| —6 |
—1 |
4 |
1 |
—3 |
0 |
| 0 |
0 |
1 |
0 |
0 |
0 |
| 0 |
0 |
0 |
1 |
0 |
0 |
| 0 |
0 |
0 |
0 |
1 |
0 |
| 0 |
0 |
0 |
0 |
0 |
1. |
Algebarski komplementi elemenata u bilo kojem od pripisanih redaka daju po jedno rješenje homogenoga reduciranog sustava; u našem dakle slučaju dobijemo ova 4 (= s — ς) rješenja:
| Za |
y |
z |
x |
v |
w |
t: |
|
| |
6 |
0 |
9 |
0 |
0 |
0 |
prvo, |
| —1 |
15 |
0 |
9 |
0 |
0 |
drugo, |
| 2 |
—39 |
0 |
0 |
9 |
0 |
treće, |
| 0 |
0 |
0 |
0 |
0 |
9 |
četvrto rješenje. |
Opće rješenje hom. reduc. sustava dobije se kao linearni spoj gornjih specijalnih rješenja t. j. tako, da gornja četiri rješenja pomnožimo po redu sa k1, k2, k3, k4 i zbrojimo (k1,..., k4 po volji); kod nas je:
y = 6 k1 — k2 + 2k3, z = 15 k2 — 39 k3, x = 9k1
v = 9k2, w = 9k3, t = 9k4
9. Vrste determinanata. Kako se det. javljaju u raznim matem. područjima, ima ih i više oblika.
I. Simetrične su det. one, koje su simetrične s obzirom na glavnu diagonalu; kod njih je dakle ajk = aki; specijalno se javljaju kod kvadratnih forma, te se zovu diskriminantama; uz svaku simetričnu det. vezana je t. zv. sekularna jednadžba 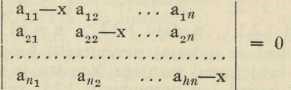
s bitnim svojstvom, da su joj svi korijeni realni.
II. Kod ortogonalnih det. je
ail ak1 + ai2 ak2 + ... + ain akn = {10 za i { =k,≠k,
t. j. skalarni produkt bilo kojeg redka sa samim sobom je = 1, a s kojim drugim redom je = 0. Vrijednost je ortogonalne det. = ± 1. Te se det. javljaju u geometriji, na pr. kod transformacija koordinata.
III. Funkcionalne ili Jacobijeve det. (jakobijani) su oblika
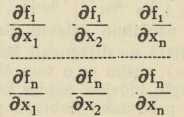
gdje su f1, f2,..., fn funkcije od n variabla x1, x2,..., xn; označuje se sa ∂ (f1, f2, ..., fn)/∂ (x1, x2, ..., xn) a ima mnogo zajedničkih svojstava s diferencijalnim kvocijentom dy/dx dolazi kod teorije implicitnih funkcija, kod transformacije višestrukih integrala, a njezino identično iščezavanje je nuždan i dovoljan uvjet, da bi funkcije f1, f2,.., fn bile među sobom funkcionalno zavisne, t. j. da bi se jedna od njih mogla izraziti s ostalima.
Ako su specijalno f1, f2 ∙, fn parcijalne derivacije neke funkcije f, onda se pripadna Jac. det. zove Hesseovom det., a javlja se kod istraživanja ekstrema funkcije f.
IV. Kod det Wrońskoga i-ti redak je ispunjen derivacijama stupnja i-l od n funkcija f1 (x), f2 (x),.., fn (x); dakle je specijalno prvi redak ispunjen tim funkcijama. Javlja se kod linearnih diferencijalnih jednačabâ i t. d.
V. U novijim istraživanjima javljaju se i det. neizmjerno velikog reda.
VI. Promatrane su i kubne det., t. j. prostorne ili kockaste sheme i det., a i det. stupnja 4, 5, 6,...
9. Ime i oznaka. Ime »determinanta« javlja se prvi put kod Gaussa (Disquisitiones arithmeticae, 1801), kad je broj b2-ac nazvao determinantom forme ax2 + 2bxy + cy2; današnji naziv »det.« u današnjem smislu potječe od Cauchyja (1812), premda je on sam d-u kasnije nazivao i »fonction alternée«; Laplace naziva g. 1772 d-u rezultantom. Uobičajena oznaka d-e s dva uspravna poteza | | potječe od Cayleyja (1841); Cauchy označuje det. sa Σ±a11 a22...ann; vrlo je podesna Kroneckerova oznaka |aik|, (i, k = 1,2,.., n).
10.Do pojma det. došao je prvi Leibniz (oko 1678), a u pismu markizu de l’Hôpitalu (28. IV. 1693) govori o pravilu, kako da se iz n + 1 jednadžbe sa n nepoznanica eliminiraju te nepoznanice; on te jednadžbe piše ovako:
10 + 11x1 + 12x2 + ... + 1n xn = O,
20 + 21x1 + 22x2 + ... + 2n xn = O,
rezultat je eliminacije (eliminanta): slika
Samom je Leibnizu više stalo do algoritma dvostrukih indeksa, nego do same det.; djelo mu je inače bilo palo u zaborav. Do det. je g. 1683 došao Japanac Seki Kōwa. Pravim se pronalazačem det. smatra Gabriel Cramer (Introduction à l analyse des courbes algébriques, 1750), i to rješavajući n linearnih jed. sa n nepoznanica, te našavši današnje Cramerovo pravilo. Cramerovo djelo nastaviše: Vandermonde, Laplace, Lagrange, Gauss, Binet. Cauchy je 1812 u jednoj raspravi prvi dao sustavnu teoriju det., bez obzira na primjene, a u opsegu, u kojem se one obično danas uče. Široko polje primjenjivanja det. našao je Jacobi 1841. Promatranjem linearnih transformacija (Cayley, Sylvester), kvadratnih forma (Weierstrass, Frobenius) dobile su d-e nov snažan poticaj. Istraživanja o beskonačnim det. (Hill. i Poincaré 1886, Koch) i matricama nalaze danas primjenu u različnim granama matematike (integralne jednadžbe, lin. sustavi s neizmjerno mnogo nepoznanica i dr.) i teoretske fizike (na pr. kvantna teorija).
BIBL.: A. Cauchy, Mémoire sur les fonctions qui ne prennent que deux valeurs égales et de signes contraires... (1812, izd. 1815 u Journal de l’Ecole Polytechnique), to je prvo sistematsko djelo; Brioschi, La teoria dei determinanti e le sue applicazioni, Pavia 1854 (to je prva knjiga o det.); R. Baltzer, Theorie und Anwendungen der Determinanten, Leipzig 1857; G. Dostor, Eléments de la théorie des déterminants, Pariz 1877; Kowalewski, Einführung in die Determinantentheorie, Leipzig 1909; M. Lecat, Leçons sur la théorie des déterminants à n dimensions, Gand 1910; Th. Muir, The Theory of Determinants in the Historical Order of Development, I-IV, London 1906—1920.Đ. K.
2. Determinanta u biologiji je prema nazivlju A. Weismanna živa čestica, koja je nosilac neke nasljedne osobine. Po Weismannovoj teoriji nasljeđivanja nasljedna se svojstva prenose zametnom plazmom (Keimplasma), koja se nalazi u jezgrama rasplodnih stanica i stanica zametnog puta (Keimbahn), t. j. one stanične loze, koja vodi u razvitku od oplođenog jajeta do rasplodnih stanica budućeg organizma. Svako je nasljedno svojstvo zastupano u zametnoj plazmi jednom determinantom, koja se izgrađuje iz biofora (βίος »život«, φέϱω »nositi«), živih skupova organskih molekula. U determinantama Weismann je intuitivno predvidio one nasljedne faktore, koje danas zovemo geni. Da postoje kao nosioci pojedinih nasljednih svojstava realne tvarne čestice, Weismann je zaključio po tome, što ima varijetetâ, koji se baš samo u jednom svojstvu razlikuju, a inače su sasvim jednaki, što znači, da se svako svojstvo neovisno prenosi, pa mora biti svako posebice zastupano nekim čimbenikom u zametnoj plazmi. Determinante za sve osobine cijelog organizma složene su u skupove, koje Weismann zove ide (εἶδος »slika«); u njima bi bio dakle potencijalno sadržan cijeli organizam. Što je najvažnije, Weismann je ispravno došao do zaključka, da se nosioci nasljedstva nalaze u kromosomima (v.) stanične jezgre, ali je držao, da su nasljedni faktori za cijeli organizam obično više puta zastupani u kromosomima. Manji kromosomi, drži, da se sastoje iz jednog ida, a veći iz više ida, pa ih zato zove idantima. Stvaranje organizma u razvitku Weismann predočuje sebi tako, da se jezgre dijele »nasljedno nejednako« (erbungleich), naime da jedna stanica mladica dobije jedan dio determinanata stanice matice, a druga stanica mladica drugi dio, pa se to nastavlja kod daljnih dioba, sve dok napokon ne nastanu stanice, koje imaju samo još jednu determinantu, koja tada stupa u djelatnost i određuje stvaranje dotične osobine. Samo u lozi zametnog puta stanice dobivaju i predaju dalje sve determinante, tako da su onda i rasplodne stanice opremljene svim determinantama. Poteškoćama, koje čine toj teoriji pojave regulacija u embrionalnom razvitku i regeneracije, Weismann je pokušao izbjeći pomoćnom hipotezom o naknadnim determinantama, koje ipak dobivaju sve stanice. To je bila već u početku slaba strana te teorije. Ma da se poslije pokazalo, da osim nekih izuzetaka nema nasljedno nejednakih dioba staničnih jezgra, nego da nasljedni mehanizam drukčije djeluje, Weismann je ovom svojom teorijom dao mnogo pobuda, pa se ima u velike zahvaliti toj teoriji, da je nakon ponovnog otkrića Mendelova zakona nasljeđivanja tako gotovo ispravno shvaćen tvarni supstrat nasljeđivanja, kromosomi, i njihova građa iz diskretnih čestica, koje su nosioci pojedinih nasljednih obilježja.
Bez obzira na Weismannovu teoriju d. se i danas često upotrebljava kao naziv za čimbenike, koji određuju razvitak pojedinih svojstava organizma.
LIT.: A. Weismann, Das Keimplasma. Eine Theorie der Vererbung, Jena 1892; A. Weismann, Vorträge über Descendenztheorie, 2. izd., Jena 1904.B. Z-k.