DESKRIPTIVNA GEOMETRIJA ili opisno mjerstvo. — To je ona grana geometrije, kojoj je glavni zadatak, da trodimenzionalne objekte predočuje s pomoću dvodimenzionalnih slika, t. zv. projekcija u ravnini, i to tako, da se iz ovih dade objekt u prostoru jednoznačno rekonstruirati pogledom na svoje mjesto i veličinu. Drugi zadatak deskriptivne geometrije sastoji se pak u tome, da od trodimenzionalnih objekata gradi opet trodimenzionalne slike, t. zv. modele. Za postizavanje onog prvog cilja postoji u deskriptivnoj geometriji nekoliko metoda, od kojih su jedne udešene tako, da slike, dobivene s pomoću njih, sačuvaju odnošaje veličine na štetu zornosti, dok je drugima glavno upravo to, da daju zorne slike, t. j. takve, koje u gledaocu pobuđuju približno isti utisak kao i sam originalni objekt; dakako, da to ide na račun vjernosti veličinskih odnošaja.
 Sl. 1.
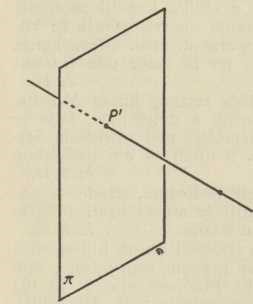
Sl. 1.Najvažnije metode deskriptivne geometrije jesu: 1. kotirana projekcija, 2. metoda projiciranja na dvije ravnine ili t zv. Mongeova metoda, 3. kosa projekcija, 4. aksonometrija i 5. centralna projekcija s perspektivom. Zajednička karakteristična operacija svih tih metoda jest projiciranje (proiicio od pro-iacio »naprijed baciti«), a sastoji se u tome, da svakom točkom zadanoga objekta u prostoru povučemo po izvjesnom propisu neki pravac, t. zv. zraku projiciranja, i odredimo njezino probodište sa zadanom ravninom (sl. 1), na kojoj želimo imati sliku onoga objekta. Po tome pak, kakav je međusobni položaj zraka projiciranja za pojedine točke objekta, dijele se metode deskriptivne geometrije najprije u dvije glavne skupine: ako sve te zrake izlaze iz jedne iste točke (centar ili središte projiciranja), projiciranje se zove centralno, a ako su sve među sobom paralelne (smjer projiciranja), tada je ono paralelno (ovo se može shvatiti i kao specijalan slučaj centralnoga, i to onaj, kada je središte projiciranja neka neizmjerno daleka točka prostora). Do daljnje podjele metoda dolazimo u skupini paralelnog projiciranja pogledom na položaj zraka projiciranja prema ravnini slike: ako su one okomite na nju, projiciranje je ortogonalno ili normalno, inače je koso. I raspored, po kojem se radi u svim metodama deskr. geometrije, uvijek je isti: Pošto je opisana bit metode, prelazi se na predočivanje triju osnovnih prostornih elemenata: točke, pravca i ravnine. Iza toga se rješavaju temeljni zadatci, t. j. oni, na koje se kao sastavne dijelove dade rastaviti svaki složeni zadatak deskriptivne geometrije. Dvije su vrsti temeljnih zadataka: a) oni, kod kojih se radi samo o spajanju i sijeđenju točaka, pravaca i ravnina (to su t. zv. projektivni zadatci), b) oni, kod kojih se radi o pravim veličinama dužina, kutova, likova i t. d. (to su metrički zadatci). Među projektivne uzimaju se i zadatci o paralelizmu pravaca i ravnina, premda su to zapravo zadatci afine prirode, a u grafičkom pogledu mogu biti čak i metrički, i to onda, kada bismo trebali paralele crtati samo s pomoću jednog ravnala i šestara; no jer u deskriptivnoj geometriji i uopće u običnom geometrijskom crtanju operiramo redovito ne s jednim ravnalom nego s dva trokuta, a s pomoću ovih se paralele crtaju izvanredno jednostavno (gotovo kao spojnice dviju točaka), to se zbog toga i zadatci o paralelama ubrajaju u projektivne. Tako ostaje kao grafička karakteristika metričkih zadataka ortogonalitet (okomitost) i uporaba šestara.
 Sl. 2.
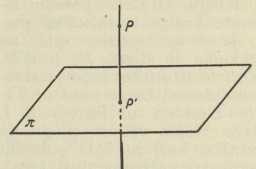
Sl. 2.Kotirana projekcija. — U toj metodi imamo samo jednu ravninu, na koju projiciramo; označujemo je sa π. Sliku ili projekciju neke točke P prostora određujemo tako, da točkom P povučemo okomicu na ravninu π, te odredimo njezino probodište P' sa π (sl. 2); to je probodište P' projekcija točke P na ravninu π. Pravac PP' zove se zraka projiciranja točke P, a dužina P'P (računata uvijek od projekcije P' prema originalnoj točki P) kota točke P (zapravo je to udaljenost točke P od ravnine slike π); po tom se nazivu onda zove i čitava metoda kotiranom projekcijom. Zbog toga pak, što je zraka projiciranja PP' okomita ili ortogonalna na ravnini slike, spada ta metoda među ortogonalne projekcije. U kotiranoj projekciji je dakle točka određena sa dva podatka: projekcijom i kotom; ova pak može biti zadana ili grafički (dakle u naravi, kao dužina) ili numerički (kao broj), a u tom slučaju mora biti zadana još i jedinična dužina. Važno je pri tom, da je originalnom točkom P u prostoru projekcija P' jednoznačno određena, dok obrnuto ne vrijedi, jer točku P' u ravnini π ima kao svoju projekciju ne jedna točka prostora, nego neizmjerno mnogo njih, naime sve točke na okomici, dignutoj u P' na π. Kota točke P može biti pozitivna ili negativna, prema tome, na kojoj se strani ravnine π nalazi točka P; pritom se kao pozitivna strana ravnine π može uzeti po volji jedna od dviju mogućih. Projekcijom i kotom (uz eventualnu jediničnu dužinu) originalna je točka jednoznačno određena, te je tako uspostavljena recipročno jednoznačna korespondencija između originalnih točaka u prostoru i njihovih kotiranih projekcija u ravnini. — U crtnji se ona dva podatka točke P zadaju tako, da se uz točku, koja znači projekciju točke P stavi slovo P' i uza nj u okrugle zagrade kota kao broj, a posebno još i jedinična dužina. U našoj se slici 3 originalna točka P dakle nalazi na okomici dignutoj u točki P' na ravninu π (t. j. na ravninu papira), udaljena za četiri dužine e iznad papira (jer se obično ta strana horizontalne ravnine π uzima kao pozitivna; ako je π vertikalno, kao na pr. ploča, tada se kao pozitivna uzima prednja strana). — Pravac g predočuje se u kotiranoj projekciji tako, da najprije njime položimo ravninu okomitu na π (ravnina projiciranja za pravac g), te odredi njezina presječnica g' sa π; g' je (ortogonalna) projekcija pravca g na ravninu slike π. No premda je g' jednoznačno određeno sa g, obrnuto ne vrijedi, jer svaki pravac u ravnini, dignutoj pravcem g' okomito na π, ima svoju projekciju u g'. Da bude g određeno, treba osim g' znati još nešto, a to je točka G, u kojoj pravac g probada ravninu slike π, t. zv. probodište pravca g, te prikloni kut pravca g prema ravnini π, t. j. kut α = (g'g). U grafici se to prikazuje tako, da ravninu projiciranja preložimo, t. j. rotiramo oko g' za 90° u ravninu π; s njom ide i pravac g, i to tako, da probodište G ostaje na miru, a prikloni se kut α nakon rotiranja prikazuje u pravoj veličini; preloženi pravac g označuje se sa (g) (sl. 4). I opet je na taj način osigurana recipročno jednoznačna korespondencija između originalnih pravaca prostora i njihovih kotiranih projekcija u ravnini π. — Napokon se neka ravnina ρ predočuje u kotiranoj projekciji s pomoću svoga traga r (to je presječnica ravnine slike π s ravninom ρ, dakle r≡π×ρ) i priklonoga kuta β = (πρ). Taj se kut određuje ovako: položi se bilo koja ravnina φ, okomita na tragu r (t. zv. profitna ravnina ravnine ρ), pak se odrede njezine presječnice f i p s ravninama π i ρ; tada je prikloni kut β = (fp). Pravac f trag je profilne ravnine, a p se zove priklonica ravnine ρ. U crtnji se to prikazuje tako, da profilnu ravninu preložimo oko njezina traga f u π (pritom je, dakako, f okomito na r) (sl. 5). Vrlo lako se možemo opet uvjeriti, da je na taj način osigurana recipročno jednoznačna korespondencija između originalne ravnine ρ i njezinog predočenja u kotiranoj projekciji. — Pošto su tako predočene u kotiranoj projekciji općene točke, pravci i ravnine, treba još to pokazati i za specijalne položaje tih elemenata; a to su ovi: točka leži u π, pravac, odnosno ravnina, okomiti su na π, odnosno paralelni sa π. No u te pojedinosti ovdje ne možemo ulaziti.
 Sl. 3.
Sl. 3.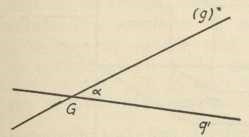 Sl. 4.
Sl. 4.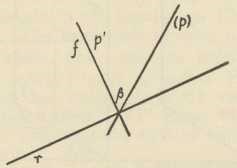 Sl. 5.
Sl. 5.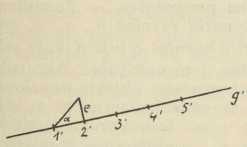 Sl. 6.
Sl. 6.Isto tako samo ćemo sumarno navesti, u čem se sastoje temeljni zadatci. Projektivni su na pr.: odrediti projekciju, probodište i prikloni kut pravca g, koji je zadan sa svoje dvije točke A, B (svaka od njih zadana dakako svojom projekcijom i kotom), ili: odrediti trag i prikloni kut ravnine ρ, koja je zadana a) sa svoje tri točke A, B, C, odnosno b) jednom točkom A i pravcem g, ili: odrediti presječnicu dviju ravnina, odnosno probodište pravca i ravnine, i t. d. Kod rješavanja tih zadataka odlučne su sutražnice ravnine, t. j. pravci ravnine, paralelni s njezinim tragom. — Od metričkih zadataka spomenut ćemo samo ove: odrediti pravu veličinu dužine AB, od koje su zadane krajne točke svojim projekcijama i kotama (prelaganje trapeza AA'B'B oko A'B' u π); odrediti pravu veličinu trokuta ABC, koji leži u zadanoj ravnini ρ; odrediti udaljenost točke P od ravnine ρ, i t. d. Kod rješavanja ovih zadataka važne su osim sutražnica još i priklonice ravnine, a od grafičkih operacija rotiranje ravnine oko traga u ravninu π (t. zv. nul-preložaj), jer se nakon toga rotiranja sve, što se nalazi u dotičnoj ravnini, vidi u preložaju u pravoj veličini. Kod konstrukcije toga preložaja neprestano se služimo t. zv. afinitetom, t. j. geometrijskom srodnošću, koja, postoji između projekcije i preložaja, a sastoji se ovdje u tome, da su 1) spojnice korespondentnih točaka (t. j. projekcije P' točke P ravnine ρ i preložaja P0 te točke P) sve među sobom paralelne (naime okomite na tragu r), to su zrake afiniteta, i 2) da se korespondentni pravci (t. j. projekcija g' pravca g ravnine ρ i preložaj g0 toga pravca g) sijeku na tragu r, to je os afiniteta. S pomoću toga pojednostavnjuju se izvanredno konstrukcije u čitavoj deskriptivnoj geometriji.
Sada se ti temeljni zadatci primjenjuju na rješavanje složenih zadataka, među kojima su osobito važni: predočivanje tjelesa (uglastih i oblih) u kotiranoj projekciji; određivanje njihovih presjeka nekom ravninom, odnosno među sobom (prodori i zadori), te konstrukcija sjena za paralelno, odnosno centralno osvjetljenje. Kod konstrukcije presjeka piramida i stožaca nekom ravninom vrlo nam dobro dolazi jedno drugo geometrijsko srodstvo, t. zv. kolineacija, koja se ovdje sastoji u tome, da 1) spojnice korespondetnih točaka idu sve jednom istom točkom (središte kolineacije) i 2) da sjecišta korespondentnih pravaca leže sva na jednom istom pravcu (os kolineacije). Što se tiče sjena, njihova se konstrukcija svodi na određivanje probodišta pravca i ravnine, odnosno pravca i neke druge plohe; jer sjena neke točke P prostora na neku plohu određuje se tako, da se tom točkom P povuče zraka svjetlosti i odredi probodište te zrake s onom plohom.
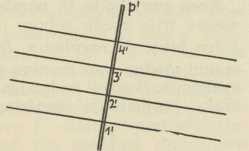 Sl. 7.
Sl. 7.Pripomenuti treba još, da se pravci ravnine predočuju u kotiranoj projekciji na gore opisani način u teoretskoj deskriptivnoj geometriji, dok je u praksi, t. j. u primjeni te metode na tehničke nauke to predočivanje ovakvo: zada se projekcija g' pravca g i na njoj projekcije 1', 2', 3', ... onih točaka njegovih, koje imaju kotu 1, 2, 3,... (sl. 6); dakako, još mora biti zadana i jedinična dužina e, pa je tada određen i prikloni kut α pravca; dužina 1'2'=2'3'= ... zove se interval pravca. Tako zadani pravac zove se graduirani pravac. Ravnina pak ρ predočuje se tako, da zadamo jednu njezinu graduiranu priklonicu, ali se ova za razliku od običnoga pravca iscrtava dvostruko (sl. 7); pravci, povučeni točkama 1', 2', 3',... projekcije p' priklonice p okomito na p', projekcije su sutražnica te ravnine; u praksi se one zovu slojnicama ili izohipsama. S pomoću ovih predočenja temeljni se zadatci (a onda i složeni) rješavaju često vrlo jednostavno.
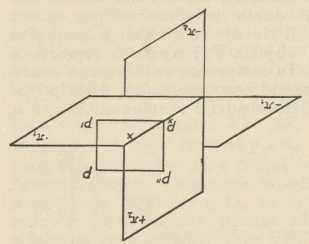 Sl. 8.
Sl. 8.Mongeova metoda. — Ovdje imamo dvije ravnine slike, t. j. dvije ravnine π1 i π2, na koje projiciramo, te se uzima da je π2 ⊥ π1; ravnina π1 je uvijek horizontalna, a π2 onda vertikalna, i to frontalna, t. j. paralelna s čelom. Presječnica tih dviju ravnina zove se os x, te dijeli svaku od njih u dva dijela; prednji dio ravnine π1 i gornji dio ravnine π2 smatramo pozitivnima, a ostala dva negativnima. Točka P prostora ima sada dvije (ortogonalne) projekcije: P' na π1 i P" na π2 (sl. 8). Zrake projiciranja PP', PP" određuju ravninu, okomitu na os x; ona siječe os x u točki Px kao četvrtom vrhu pravokutnika PP'PxP". Međutim, u svrhu crtanja moraju se te dvije projekcije dovesti u jednu ravninu, naime u ravninu, u kojoj crtamo; kao takva uzima se π1, pak se π2 sa svim, što je u njoj, preloži oko osi x u π1, i to tako, da +π2 padne na —π1 (ako crtamo na vertikalnoj ravnini π2, na pr. na ploči, tada preložimo π1 u π2, i to tako, da +π1 padne na -π2). Pritom će stranice PxP' i PxP" onoga pravokutnika pasti u jedan pravac, okomit na os x, koji se zove ordinala točke P (sl. 9); jasno je, da nam dužina PxP' znači udaljenost originalne točke P od ravnine π2, a dužina PxP" njezinu udaljenost od ravnine π1. Ako je točka P u prvom kvadrantu, t. j. u onom dijelu prostora, koji je omeđen poluravninama + π1 i + π2, tada je P' ispod osi x, a P" iznad nje; točka P u drugom kvadrantu ima obadvije projekcije iznad osi x, u četvrtome obadvije ispod, a u trećem prvu projekciju iznad, a drugu ispod osi x. I u ovoj metodi postoje kote (i to dvije, to su upravo one udaljenosti točke P od ravnina projekcija π1 i π2), ali one više nemaju kod određivanja točke P s pomoću projekcijâ one uloge, koju je imala kota u kotiranoj projekciji. Sada su naime već samim projekcijama P',P" (vezanima dakako uvjetom, da leže na istoj ordinali) one suodređene. A upravo je druga ravnina slike π2 i uvedena zbog toga, da eliminira kotu kao nezgodan grafički elemenat, te da je nadomjesti drugom projekcijom i time sve svede na čistu geometriju, odnosno grafiku. — Rekonstrukcija originalne točke P iz njezinih projekcija izvodi se tako, da najprije ravninu π2 (na ploči ravninu π1 dovedemo u njezin originalni položaj, a onda u projekcijama P' i P" dignemo zrake projiciranja okomito na π1 odnosno π2, pak je njihovo sjecište tražena točka P. Sve su ove operacije jednoznačne tako, da za zadani par P', P" dobivamo samo jednu posve određenu točku P baš onako, kao što smo prije iz točke P dobili jednoznačno par točaka P’, P". Prema tome postoji i ovdje recipročno jednoznačna korespondencija između objekta P i njegovih reprezentanata P', P" u projekciji. Ta recipročno jednoznačna korespondencija uopće je jedna od osnovnih načela deskriptivne geometrije. — Do ideje, da obadvije ravnine slike π1 i π2 treba dovesti u združen položaj, došao je prvi G. Monge, te je po tom postao tvorcem te metode (koja se zato po njemu i zove) i uopće osnivačem deskriptivne geometrije. — Drugi osnovni elemenat, pravac, recimo g, ima u toj metodi isto dvije projekcije g', g", ali i dva probodišta G1, G2 (sl. 10), a treći, ravnina ρ, ima dva traga r1, r2, koji se moraju iz stereometrijskih razloga sjeći na osi x (sl. 11). — Od specijalnih položaja tih triju elemenata važni su ovi: Točka leži u π1 ili π2 ili u ravnini, koja raspolavlja prvi i treći kvadrant, odnosno u onoj, koja raspolavlja drugi i četvrti kvadrant; ova se zove ravnina istovjetnosti ili identiteta, jer za svaku točku te ravnine padaju obadvije projekcije zajedno, ona se pak zove ravnina sumjernosti ili simetrije, jer su za svaku njezinu točku projekcije simetrične s obzirom na os x. Kod specijalnih položaja pravca važni su oni, gdje je pravac okomit na π1 ili π2, odnosno paralelan sa π1 ili π2, te okomit na os x, odnosno paralelan s njome; kod specijalnih pak ravnina osobito su važne one, koje su okomite na π1 ili π2, i to zato, što se tada sve, što je u takvoj ravnini, projicira u prvom slučaju na π1 u prvi trag, a u drugom na π2 u drugi trag dotične ravnine; a to se dade grafički izvanredno dobro iskoristiti.
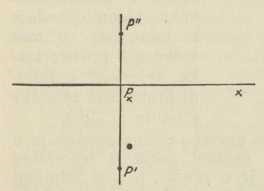 Sl. 9.
Sl. 9.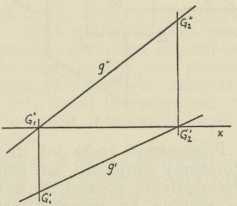 Sl. 10.
Sl. 10.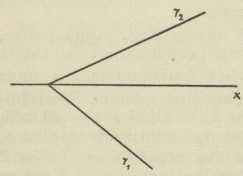 Sl. 11.
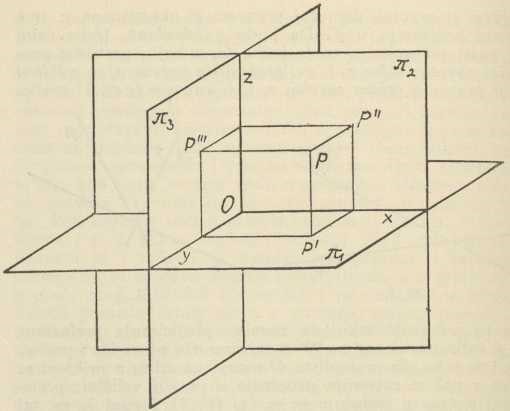
Sl. 11.U nekim slučajevima uvodi se i treća ravnina slike π3, okomita na prve dvije, dakle i na os x kao njihovu presječnicu. Tada ima svaka točka P prostora tri projekcije P', P", P'", svaki pravac g tri projekcije g', g", g'" i tri probodišta G1, G2, G3, a svaka ravnina ρ tri traga r1 r2, r3. Dakako, da je uvijek jedan od ta tri elementa prekobrojan, jer su općeno već dva dovoljna za određenje točke, pravca, odnosno ravnine u prostoru. Ravnina π3 zove se bokocrtna ravnina, dok se π1 zove tlocrtnom, a π2 nacrtnom; prema tome se onda i tri projekcije zovu redom tlocrt, nacrt i bokocrt. Ravnine π1 i π3 sijeku se u osi y, a ravnine π2 i π3 u osi z, dok se zajednička točka O svih triju osi zove ishodište (sl. 12). S pomoću toga sustava od tri ravnine π1, π2, π3, odnosno tri osi x, y, z, može se svaka točka P prostora zadati sa tri broja — kote x, y, z, od kojih prva znači udaljenost točke P od ravnine π3 (u smjeru osi x!) i t. d.; svaka pak ravnina ρ prostora može se zadati isto sa tri broja, koji znače odsječke, što ih ta ravnina čini na osima x, y, z. Pravac se ne može zadati direktno s ovakva tri broja, nego indirektno tako, da se zada kao spojnica dviju točaka ili kao presječnica dviju ravnina. (Zapravo imamo tu posla s jednim prostornim koordinatnim sustavom.) — Od zgode do zgode upotrebljavaju se u Mongeovoj metodi još i t. zv. stranocrti, to su ravnine, okomite na π1 ili π2 ili π3, ili na kojem već prije toga uvedenom stranocrtu, a uvode se u konstrukcije zbog toga, što se s pomoću njih može znatno pojednostavniti rješenje nekog prostornog problema (to su t. zv. transformacije u deskriptivnoj geometriji).
 Sl. 12.
Sl. 12.Što se tiče zadataka (bilo temeljnih, bilo složenih) i njihove primjene na obrađivanje tjelesa, njihovih presjeka i sjena, vrijedi isto, što smo kazali kod kotirane projekcije. A razumije se, da će sama rješenja tih zadataka, odnosno primjena u grafici teći sada drugačije nego tamo, upravo zbog druge prirode ove metode.
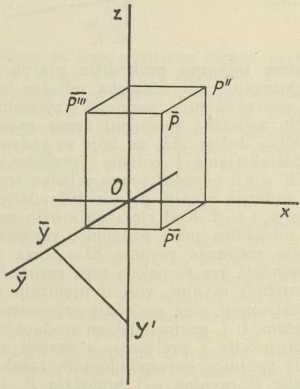
Kosa projekcija ili paralelna perspektiva. — Zamislimo sustav triju među sobom okomitih ravnina π1, π2, π3 položen tako, da ravnina π2 leži u ravnini crtnje π, koju uzimamo ujedno kao ravninu slike, i to vertikalno. Ako tada svakom točkom P zadanoga prostornoga objekta povučemo zraku projiciranja paralelno sa zadanim smjerom s, koji je kos prema π, bit će probodište P te zrake sa π kosa projekcija ili paralelna perspektiva točke P na ravninu π; a dosljedno ima onda i čitav zadani objekt izvjesnu kosu projekciju na ravnini slike π≡π2. Pritom je važno prije svega to, da od tri osi x, y, z prva i treća leže u ravnini slike, i zato su njihove kose projekcije s njima istovjetne, dok os y, jer leži izvan ravnine slike, ima kao kosu projekciju izvjesni pravac y kroz ishodište O, koji je priklonjen prema osima x i z (sl. 13); pod kojim kutevima, to zavisi o smjeru projiciranja s. Ovaj se pak u crtnji fiksira tako, da na originalnoj osi y, recimo ispred ravnine π, odaberemo po volji točku Y i odredimo njezinu kosu projekciju Y na y, tada naime u pravokutnom trokutu OYY (pravi kut je kod O, budući da je os y okomita na π) hipotenuza YY daje smjer kosoga projiciranja. Ako zamislimo ravninu π1 združenu s ravninom π2 na način, kako smo to izveli u Mongeovoj metodi, tada će točka Y doći u točku Y' na preloženoj osi y (u grafici: na doljnjem dijelu osi z, v. sl. 13), pak je tako nastali trokut OYY' bitno važan za izvođenje konstrukcija u ovoj metodi; zove se zato temeljnim trokutom. Omjer OY/OY = OY/OY' = p zove se prikrata kose projekcije, jer nam naznačuje, kako se prikraćuju u našem kosom projiciranju sve dužine, okomite na ravninu slike π (t. zv. dubine prostora). O numeričkoj vrijednosti te prikrate zavisi slikovitost ili zornost slike zadanoga predmeta; obično se uzima, da je p jednako ½ ili ⅔ ili 3/4 i t. d., no može biti i p = 1 ili čak > 1, samo što su tada slike deformirane, jer dubine nisu prikraćene, nego produljene. — Točkom P prostora određena je kosa projekcija P jednoznačno, ali obrat ni tu ne vrijedi, jer je kosom projekcijom P određena samo zraka projiciranja, pak svaka točka na njoj može značiti originalnu točku P. Za jednoznačno određenje točke P treba dakle uz P zadati još nešto; u tu svrhu služi jedna od triju ortogonalnih projekcija P', P", P'", od kojih je druga odmah i svoja kosa projekcija, dok je P' različito od P', odnosno P' " različito od P"'. U slici 13 predočeno je, u kojem se odnošaju nalaze te četiri projekcije P, P', P", P' " pak je odmah jasno i to, da su bilo kojim dvjema od njih ostale dvije određene. — Slično ima i svaki pravac g prostora četiri projekcije g, g', g", g' ", pak su i tu za određenje originalnog pravca nužne i dovoljne dvije od njih; osim toga ima pravac i tri probodišta, u kosoj su projekciji to G1, G2, G3 — Općena ravnina ρ prostora predočena je u kosoj projekciji s bilo koja dva od svoja tri traga r1, r2, r3. — Za specijalne položaje tih triju osnovnih elemenata kao i za temeljne, odnosno složene zadatke i njihove primjene na predočivanje tjelesa te njihovih presjeka, prodora i sjena, vrijedi ono, što je rečeno kod prvih dviju metoda uz pripomenu, da se rješavanje svih tih zadataka sada udešava prema biti sadašnje metode. Kao osobitost kose projekcije u tom pogledu spomenut ćemo samo to, da je slika kugle elipsa, a ne kružnica kao u prvim dvjema metodama.
 Sl. 13.
Sl. 13.Posebno treba spomenuti jedan specijalni slučaj kose projekcije, naime onaj, gdje pozitivna os y čini s negativnom osi x kut od 45°, a prikrata je = 1. Ta se kosa projekcija zove kavalirna perspektiva (zbog izvjesnih dijelova na najvišim mjestima utvrda, koji su se zvali kavalirima); ta se metoda mnogo upotrebljavala u nauci o fortifikaciji, pak se zato često zove i vojnom perspektivom (Militärperspektive), ali se pod tim nazivom razumijeva jedna druga vrst kose projekcije. Prednosti kavalirne perspektive jesu: vanredna jednostavnost konstrukcije slika i savršena metričnost, jer se iz njezinih slika mogu sve tri dimenzije predočenih predmeta oduzeti iz slike direktno u pravoj veličini. Ne smeta mnogo, što pritom nešto strada slikovitost projekcije, budući da se čini, da su svi predmeti produljeni u smjeru dubine, t. j. u smjeru okomitom na ravninu slike.
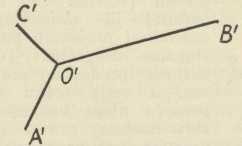 Sl. 14.
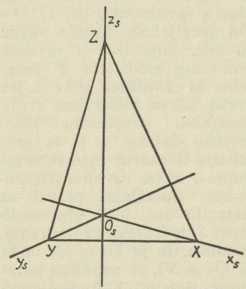
Sl. 14.Aksonometrija. — I ovdje uzimamo sustav triju ravnina π1, π2, π3, odnosno triju osi x, y, z kao temelj, na koji protežemo prostorne objekte, koje treba predočiti slikom, ali sada stavljamo taj sustav u općeni, t. j. kosi položaj prema ravnini π, na kojoj crtamo, a ne kao prije, gdje je bilo π1≡ π2. Nakon toga sve, t. j. objekt zajedno sa sustavom Oxyz projiciramo na ravninu π; pritom će se osi x, y, z projicirati u tri pravca xs, ys, zs kroz Os, a prostorna figura F u Fs, pak je tu bitno, da će kod konstrukcije slike s biti važne baš te tri osi xs, ys, zs. Zbog toga se ova metoda i zove aksonometrijom (axis = os); a jer se spomenuto projiciranje može izvesti na tri različita načina, ortogonalno, koso ili centralno, imamo i odnosne vrste: ortogonalnu, kosu i centralnu aksonometriju. Ova posljednja ne upotrebljava se gotovo nikada, kosa ne baš mnogo, ali ortogonalna gotovo redovito. U kosoj imamo izvanredno važni Pohlkeov stavak (t. zv. fundamentalni stavak aksonometrije), koji glasi: Ako u ravnini zadamo tri dužine O'A' O'B' O'C' po veličini i smjeru posve po volji (sl. 14), tada uvijek postoje u prostoru tri među sobom okomite i jednake dužine OA, OB, OC, od kojih su one tri zadane dužine kose projekcije; jedino ograničenje jest to, da sve četiri točke O, A, B, C ne leže na jednom istom pravcu. To je možda najljepši stavak deskriptivne geometrije, a dao ga je K. Pohlke g. 1853 bez dokaza; elementarni dokaz dao je g. 1864 H. A. Schwarz, a za njim je slijedio velik broj drugih. Taj stavak ne vrijedi za ortogonalnu aksonometriju, jer je u ovoj smjer projiciranja fiksiran, naime okomit na ravninu slike π. Tu se osi temeljnog sustava Oxyz predočuju u aksonometrijskoj slici kao visine trokuta XYZ, gdje su X, Y, Z probodišta osi x, y, z s ravninom slike π (sl. 15); stranice XY, XZ, YZ toga trokuta presječnice su ili tragovi ravnina π1, π2, π3 s ravninom π, te se zbog toga taj trokut zove trokut tragova; mi ćemo ga zvati čelnim trokutom. Originalno ishodište O nalazi se na zraci projiciranja, dignutoj u Os na ravninu π (t. j. na papir), redovito iza te ravnine; njezina udaljenost OsO od ravnine π lako se dade odrediti. Prije nego što se ide crtati u ortogonalnoj aksonometriji, treba imati aksonometrijske slike jediničnih dužina za osi Ox, Oy, Oz; to se određuje s pomoću prelaganja ravnina π1, π2, π3 oko spomenutih tragova u ravninu π (sl. 20). To je važno zbog toga, što treba znati prikrate dužina, koje imaju smjer tih osi. Ove su prikrate zbog ortogonalnog projiciranja manje od 1, a zbroj njihovih kvadrata = 2. Prema međusobnom odnošaju prikrata imamo ove vrsti ortogonalne aksonometrije: izometričku, ako su sve tri prikrate među sobom jednake, dimetričku ili monodimetričku, ako su samo dvije od njih jednake, te trimetričku ili anizometričku, ako ni koje dvije prikrate nisu među sobom jednake (čelni je trokut u tim slučajevima istostraničan, istokračan, odnosno raznostraničan). — Predočivanje točaka, pravaca i ravnina kao i rješavanje temeljnih projektivnih zadataka ide gotovo jednako kao u kosoj projekciji, a rješavanje metričkih zadataka uz izvjesne promjene. Ta suglasnost međutim nije slučajna, nego izvire odatle, što je kosa projekcija zapravo specijalni slučaj kose aksonometrije, i to upravo onaj, kada je ravnina slike π identična s ravninom π2. Jedan drugi specijalni slučaj jest već spomenuta vojna perspektiva, koja se često zamjenjuje kavalirnom perspektivom; sastoji se u tome, da je ravnina slike π sada u ravnini π1 (dakle os z okomita na π), a prikrata za os z jednaka 1 tako, da se i tu sve tri dimenzije objekata vide u slici u pravoj veličini. U kristalografiji upotrebljava se posebna vrst kose aksonometrije: ravnina slike π položena je vertikalnom osi z, ali tako, da je kosa prema ravninama π2 i π3.
 Sl. 15.
Sl. 15.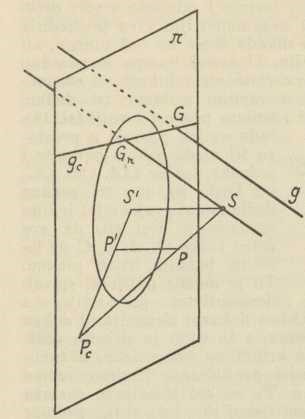 Sl. 16.
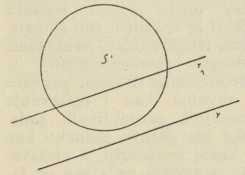
Sl. 16.Centralna projekcija i perspektiva. — Najprije treba fiksirati međusobni položaj središta projiciranja S prema ravnini slike π; to se čini tako, da se odredi ortogonalna projekcija S' od 5 na π i onda u π oko S' opiše kružnica s polumjerom SS' (si. 16); točka S' zove se glavna točka, a ona kružnica kružnica distancije, jer se dužina SS' zove distancija centralne projekcije. Točka P prostora predočuje se u toj metodi tako, da se odredi probodište Pc ravnine slike π sa zrakom projiciranja SP. Centralna projekcija Pc točke P određena je originalnom točkom P jednoznačno, ali obrat opet ne vrijedi, nego se osim Pc mora zadati još jedan podatak. Kao takav mogla bi služiti ortogonalna projekcija P' točke P na π; u tom bi slučaju dakako tri točke S', P', Pc morale ležati na jednom istom pravcu (sl. 16). No u općenoj ili slobodnoj centralnoj projekciji postupamo drugačije. Tu najprije predočimo pravac, a onda točku s pomoću njega kao njezina nosioca; pravac g prostora pak predočujemo u centralnoj projekciji tako, da odredimo njegovo probodište G u ravnini slike π, središtem projiciranja S povučemo paralelu s pravcem g i odredimo njezino probodište Gn s ravninom slike (to je zapravo centralna projekcija neizmjerno daleke točke pravca g); spojnica GGn centralna je projekcija gc pravca g (sl. 16). Točka Gn zove se nedogled, a pravac SGn nedogledna zraka pravca g. Odmah je jasno, da je probodištem i nedogledom originalni pravac g jednoznačno određen: treba samo točkom G povući pravac, paralelan sa spojnicom SGn. Tako je utvrđena recipročno jednoznačna korespondencija između originalnog pravca g i para točaka G, Gn. Ako sada na pravcu g uzmemo bilo koju točku P, bit će njezina centralna projekcija Pc na gc, pak ako obrnuto na gc zadamo neku točku Pc kao centralnu projekciju točke toga pravca, tada je time originalna točka P jednoznačno određena: to je sjecište originalnog pravca g (rekonstruiranoga na netom opisani način) sa zrakom projiciranja SPc. — Ravnina ρ prostora predočuje se u centralnoj projekciji s pomoću svoga traga r u ravnini π i svoje nedoglednice rn, t. j. presječnice ravnine π s nedoglednom ravninom, koja je središtem S položena paralelno s ravninom ρ (sl. 17). — Od specijalnih točaka važne su one, koje leže u ravnini, položenoj središtem S paralelno sa ravninom slike π, jer svaka takva točka ima svoju centralnu projekciju neizmjerno daleko, t. j. ta projekcija iščezava; zato se ta ravnina i zove ravnina iščezavanja. Specijalni pravci su najprije oni, koji idu središtem S, t. j. zrake projiciranja, njihova je centralna projekcija točka, te je Gn ≡ G; onda pravci okomiti na π (za njih je Gn = S'), te napokon paralelni sa π (tu su G i Gn neizmjerno daleko). Od specijalnih ravnina imamo najprije one kroz središte S (projiciraju se u svoj trag r = rn), te one, koje su okomite na π (r ide kroz S'), odnosno paralelne sa π (r i rn neizmjerno daleko); među prvima i trećima nalazi se i ravnina iščezavanja. — Grafičko rješavanje zadataka u centralnoj projekciji, a prema tome i njihova primjena, u toj su metodi posve različiti od onih u dosadašnjim metodama, jer je i sama metoda sada sasvim druge vrsti nego što su bile one, upravo zbog toga, što sada zrake projiciranja idu jednom istom točkom u konačnosti.
 Sl. 17.
Sl. 17.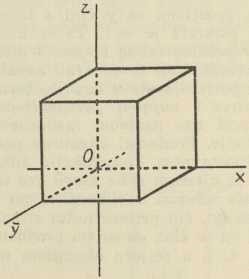 Sl. 19.
Sl. 19.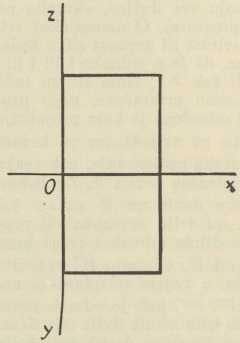 Sl. 18.
Sl. 18.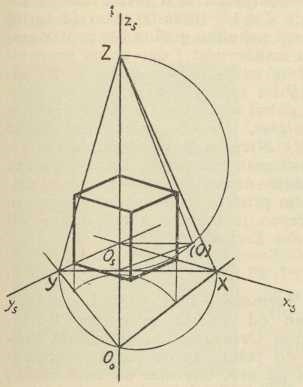 Sl. 20.
Sl. 20.Perspektiva (perspicere »gledati kroz«) daje uglavnom iste slike kao i centralna projekcija, ali se od ove razlikuje prvo po tome, što se kod nje središte S shvaća kao optičko oko (dok je kod centralne projekcije to matematička točka), pak zbog toga predočuje u slici samo ono, što se nalazi u vidnom polju oka (dok centralna projekcija predočuje i ono, što se nalazi »iza« središta projiciranja), a drugo po tome, što svoje slike izvodi ne direktno kao centralna projekcija, nego indirektno, naime iz Mongeovih projekcija dotičnog objekta. Posebne vrsti perspektive jesu reljefna i kazališna perspektiva.
Centralna projekcija dopušta neke generalizacije, tako na pr. u tom smislu, da se uzmu dva središta projiciranja, pak se određuju pripadne dvije slike zadanoga objekta, i to ili na jednu ravninu slike π ili na dvije ravnine i π2, koje su u općenom, ali fiksnom međusobnom položaju. To je t. zv. bicentralna projekcija. Posve je druge vrsti generalizacija na četverodimenzionalni prostor; ako naime u tom prostoru uzmemo kao tvorevinu, na koju projiciramo ne ravninu (kao do sada, u našem trodimenzionalnom prostoru), nego jedan ravni trodimenzionalni prostor Π kao prostor slike, tada možemo svaki zadani objekt F u četverodimenzionalnom operacionom prostoru (na pr. neki politop) projicirati iz zadanog središta S na prostor Π baš onako, kako smo dosada projicirali trodimenzionalne objekte na ravninu π (zrake projiciranja za pojedine točke i njihova probodišta sa prostorom Π). A daljnji je zadatak taj, da tu trodimenzionalnu centralnu projekciju F' projiciramo na neku ravninu π unutar prostora Π (v. H. de Vries, Die Lehre von der Zentralprojektion im vierdimensionalen Raume, Leipzig 1905). — Već smo na početku spomenuli, da se neke od ovako prikazanih metoda odlikuju svojom zornošću, a druge opet time, što se iz njih lako mogu dobiti prave veličine objekata. Za ispoređivanje tih dvaju svojstava neka služe slike 18—21, u kojima je predočena kocka redom s pomoću Mongeove metode, kose projekcije, ortogonalne aksonometrije i centralne projekcije; pritom je u prve tri slike kocka uzeta tako, da su joj tri brida u osima x, y, z, a u četvrtoj je prednja pobočka kocke u ravnini slike.
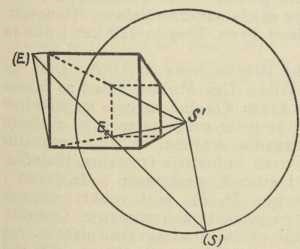 Sl. 21.
Sl. 21.U prikazu pojedinih metoda vidjeli smo, da je grafičko, konstruktivno rješavanje zadataka o prostornim figurama za svaku od tih metoda neko drugo, no valja naglasiti, da je idejno, stereometrijsko rješenje jednog istog prostornog zadatka za sve metode isto. Tako se na pr. probodište pravca i ravnine određuje svuda po istom programu: pravcem se položi bilo koja pomoćna ravnina, odredi se presječnica ove sa zadanom ravninom, te napokon sjecište te presječnice sa zadanim pravcem; no grafička provedba toga programa u svakoj je metodi drugačija.
Slikovitost ili zornost slika u svim se metodama znatno povećava s pomoću sjena prikazanih objekata. Pritom valja razlikovati bačene i vlastite sjene, a kod ovih još i rastavnice, t. j. crte na objektu, koje rastavljaju njegov osvijetljeni i tamni dio. Još jači optički efekti postizavaju se s pomoću izofota i izofenga, t. j. s pomoću crta jednakog osvjetljenja, odnosno jednake jasnoće. Na tom je polju osobito radio L. Burmester.
Ako smo naprijed neprestano spominjali samo tjelesa kao objekte projiciranja, ne znači to, da nema i drugih objekata; štaviše, ona čine samo jedan mali dio onoga, o čem radi deskriptivna geometrija. Veći dio tiče se predočivanja i istraživanja različnih krivulja i ploha, tako na pr. onih 2. stupnja, onda zavojnica, pa tračnih, rotacionih, topografskih i drugih ploha.
Priprava za učenje deskriptivne geometrije jest grafička geometrija, koja uči samu tehniku crtanja, različna pravila za osiguranje što veće točnosti, odnosno za postizavanje što veće jednostavnosti crteža, zatim izvjesne osnovne konstrukcije (na pr. pravilnih poligona) i t. d.
Deskriptivna geometrija primjenjuje se u najrazličitijim područjima: arhitekturi i drugim tehničkim strukama, nauci o siječenju kamena (stereotomiji), kartografiji, fotogrametriji, kristalografiji i t. d. Zbog toga velikog opsega njezinih primjena smatraju je neki primijenjenom matematičkom naukom, ali to nije ispravno. Deskriptivna geometrija dio je čiste matematike, jer već samo organiziranje pojedinih metoda njezinih vodi do čisto teoretskih geometrijskih problema, kako to svjedoči Pohlkeov stavak kod kose aksonometrije. Kako dubokih stvari ima tu i u Mongeovoj metodi, koja je na oko po svom pojmu jednostavna, pokazali su Nicodemi, Bordiga, Del Re i dr., a kod nas S. Šimunić (Nast. Vjesnik, knj. 30). U tim je radovima paralelno i centralno projiciranje podvrgnuto jednom zajedničkom višem principu. Daljnji je dokaz za gornju tvrdnju uloga, što je deskriptivna geometrija ima u istraživanju prostornih krivulja i ploha, pa onda u tome, što se ona dade organički posve prožeti projektivnom geometrijom (W. Fiedler), odnosno diferencijalnom geometarijom (d’Ocagne, Loria). Iz krila deskriptivne geometrije, odnosno njezinom pomoći nastao je i razvio se niz novih matematičkih nauka: tako iz perspektive projektivna geometrija, (Desargues, Poncelet, Möbius, Steiner, Staudt, Chasles), grafička statika sintezom deskriptivne i projektivne geometrije (Culmann, Cremona), ciklografija (Fiedler), kinematička geometrija (Mannheim) te fotogrametrija (Schilling). S druge je strane proučavanje odnosa originala i projekcija dovelo do trilinearnih srodnosti (Hauck) i općenog pojma korespondencije, odnosno znanstveno utemeljene metode konstruktivnog rješavanja geometrijskih problema (E. Müller). Napokon valja još istaknuti, da je bilo i pokušaja aksiomatizacije deskriptivne geometrije. Sve ovo dovoljno svjedoči, da deskriptivna geometrija nije dio praktične, primijenjene nego čiste matematike, jer se ona može općeno definirati kao ona matematička nauka, koja proučava svezu stereometrijskih relacija s planimetrijskima i to s pomoću metoda, koje su specifična njezina svojina. Najodlučniji zastupnici čisto teoretskog karaktera deskriptivne geometrije jesu Fiedler, Peschka i Loria, a kod nas J. Majcen i njegova škola.
Što se tiče koristi, koje deskriptivna geometrija pruža za praksu, to moramo povrh već gore navedenih mnogobrojnih primjena spomenuti i čisto formalnu funkciju, koju ona ima, naime razvijanje i izoštravanje prostornoga zora. Bavljenje deskriptivnom geometrijom dovodi ne samo do jasnog unutrašnjeg gledanja, nego i do visoko razvijene moći preciznog predočivanja prostornih figura i njihovih odnošaja. Upravo zbog toga je deskriptivna geometrija nuždan obučni predmet u srednjoškolskoj nastavi realnog smjera te u visokoškolskom tehničkom, odnosno čisto matematičkom studiju.
Historijat. Metoda ortogonalnog projiciranja na dvije ravnine, u obliku tlocrta i nacrta, ima svoj začetak u potrebama graditeljstva, te seže u davno doba starih Egipćana; prvi govori sasvim određeno o tome rimski graditelj Vitruvije Polion (u doba Kristovo) u djelu De architectura, u kojem navodi ihnografiju (tlocrt), ortografiju (nacrt) i scenografiju (perspektiva). Isto tako je i perspektiva potekla iz praktičnih potreba, i to slikarstva, napose za kazalište u doba Eshila (500 pr. Kr.); na zidnim slikarijama, nađenim u Pompejima i Rimu, vidi se, da su tadašnji slikari prilično poznavali nedogled i umanjivanje u daljinu. Hiparh (oko 140. pr. Kr.) našao je stereografsku projekciju za konstrukciju zemljopisnih i astronomskih karata.
Metoda tlocrta i nacrta razvila se zatim u srednjem vijeku zbog potreba siječenja kamena i gradnje svodova, te je poslije različnih pokušaja drugih autora izdao A. F. Frézier g. 1737. u Strassburgu veliko djelo u dva sveska La théorie et la pratique de la coupe des pierres et des bois ou traité de stéréotomie, u kojem je sadržana po prvi put posebno i čisto matematička teorija nekih ploha i tijela; tim je djelom stereotomija postala znanstvenom naukom. No pravom naukom učinio je metodu dviju projekcija tek G. Monge epohalnim djelom Géométrie descriptive, izašlim g. 1798 u Parizu kao plod predavanja, držanih na znamenitoj pariškoj Politehničkoj školi, koju je isti Monge osnovao g. 1795. Tu su prvi put tlocrt i nacrt združeni i kao takvi sistematski obrađeni — ideja, do koje je došao Monge već g. 1765, kao nastavnik vojne tehničke škole u Mézièresu. U tom su smjeru dalje radili Mongeovi učenici Lacroix, Hachette, Dupin, Poncelet, Chasles, Olivier (ovaj je prvi metodički upotrebljavao prelaganje i rotaciju), dok nije postigao izvjesni završetak De la Gournerie u djelu Traité de la géométrie descriptive, Pariz 1862—64.
Perspektiva je u srednjem vijeku nestala, a nadomjestila ju je paralelna perspektiva, ali je u doba renesanse opet oživjela u Italiji i Njemačkoj: L. B. Alberti (De pictura prije g. 1446; pronašao točku distancije), A. Dürer (Underweysung der Messung mit Zirckel und richtscheyt, Nürnberg 1525; konstruira perspektivne slike s pomoću tlocrta i nacrta) i G. Ubaldi (Perspectiva, Pisa 1600; pronašao nedogled). U matematičkom duhu obrađivali su perspektivu G. Desargues (Exemple de Vune des manières universelles touchant la practique de la perspective, Pariz 1636; začetnik aksonometrijske metode), B. Taylor (Linear perspective, London 1716; prvo djelo o čistoj centralnoj projekciji) i J. H. Lambert (Die freye Perspective, Zürich 1759; pokretač slobodne perspektive). Iz ideje perspektive kao metode centralnog projiciranja nastala je u 19. st. t. zv. projektivna geometrija (u svom sintetičkom obliku), kako je to već gore spomenuto.
Kosa projekcija i aksonometrija razvile su se tek u 19. st., i to u Švicarskoj (Möllinger), Njemačkoj (Weisbach, Pohlke) i osobito u Austriji (Hönig, Tilscher, Niemtschik, Staudigl, Pelz), gdje se je uopće deskriptivna geometrija osobito njegovala, u drugoj polovici toga stoljeća više nego u ijednoj drugoj zemlji, u neku ruku kao nastavak francuske Mongeove škole. Po austrijskom je uzoru bila uvedena deskriptivna geometrija i u hrvatske srednje škole i na sveučilište, te se je tu vrlo solidno obučavala sve dok nije bila ukinuta kao školski predmet (prema usmenoj izjavi G. Scheffersa, sjajnog profesora — sada umirovljenog — deskriptivne geometrije na Visokoj tehničkoj školi u Charlottenburgu, dolazili su najbolji crtači na tu školu iz Austrije i Hrvatske). U projektu je ministarstva narodne prosvjete, da se doskora deskriptivna geometrija opet uvede kao nastavni predmet u hrvatske realne gimnazije.
BIBL.: Gore spomenuta klasična djela; zatim: W. Fiedler, Die darstellende Geometrie in organischer Verbindung mit der Geometrie der Lage, 3 sv., Leipzig 4. odnosno 3. izd. 1904, 1885, 1888; Ch. Wiener, Lehrbuch der darstellenden Geometrie, 2 sv., Leipzig 1884, 1887; G. A. Peschka, Darstellende und projective Geometrie, 4 sv. Beč 1883—85; Freye Perspective, 2 sv., Leipzig, 2. izd. 1888—89; K. Rohn i E. Papperitz, Lehrbuch der darstellenden Geometrie, 3 sv., Leipzig, 3. izd., 1906; G. Loria, Lezioni di geometría descrittiva, 2 sv., Milan, 3. izd. 1919; njem. prijevod od Fr. Schüttea, Leipzig-Berlin, 1907, 1913; E. Müller, Lehrbuch der darstellenden Geometrie, 2 sv., 2. izd., Leipzig-Berlin, 1920, 4. izd. od E. Kruppe u jednom svesku 1936; Vorlesungen über darstellende Geometrie, u obradbi E. Kruppe odnosno J. L. Kramesa, 3 sv., Leipzig-Beč 1923, 1929, 1931; G. Scheffers, Lehrbuch der darstellenden Geometrie, 2 sv., Berlin 1919, 1920; F. Dalwigk, Vorlesungen über darstellende Geometrie 2 sv., Leipzig-Berlin 1911, 1914; R. Schüssler, Orthogonale Axonometrie, Leipzig 1905; J. Majcen, Opisno mjerstvo za V.-VIII. razr. realnih gimnazija, Zagreb 1919, 2. izd. 1921; J. Božičević, Linearna perspektiva, Zagreb 1942. Za povijest deskriptivne geometrije: Wiener, I. sv. gore spomenutog djela; F. J. Obenrauch, Geschichte der darstellenden und projektiven Geometrie, Brno 1897; Loria, Storia della geometría descrittiva, Milan 1921.R. C.