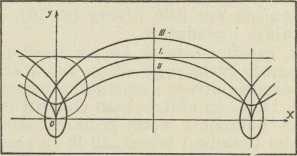
CIKLOIDA, krivulja u ravnini, nastaje ovako: Ako se kružnica u ravnini kotrlja bez sklizanja po nekom čvrstom pravcu, tada svaka točka P te ravnine, čvrsto spojena s tom kružnicom, opisuje cikloidu, i to običnu, prikraćenu odnosno produljenu prema tome, da li točka P leži na kružnici, u kružnici ili izvan nje (I, II, III u slici). Iz same definicije izlazi, da je ta krivulja periodska, t. j. sastavljena od neizmjerno mnogo sukladnih dijelova, od kojih svaki odgovara jednom potpunom okretu kružnice, koja se kotrlja. Zato je to transcendentna krivulja. Ako su x i y koordinate točke P u koordinatnom sustavu naznačenom u slici, tada parametričke jednadžbe cikloide glase:

x = rφ — d . sin φ,

gdje je r polumjer kružnice, koja se kotrlja, d udaljenost točke P od središta te kružnice, a φ kut, što ga ta udaljenost kao dužina čini s polumjerom okomitim na os x.

Obična cikloida ima za φ = 2kπ (k cio broj) šiljak (→ krivulja), prikraćena c. ima izoliranu točku (isto), a produljena uzao (isto). Duljina jednog perioda obične cikloide iznosi 8r (Wren), a za prikraćenu i produljenu izražava se ta duljina s pomoću eliptičnih funkcija (Pascal). Površina lika, omeđenog tim lukom i pripadnim dijelom osi x, jednaka je (2r² + d²) . π, dakle za običnu cikloidu 3r²π, t. j. trostrukoj površini kruga, koji se kotrlja (Roberval).

Obična cikloida je brahistohrona i tautohrona ili izohrona krivulja. Ima još i to osobito svojstvo, da je njezina evoluta opet obična cikloida.

Cikloida je posebni slučaj krivulje, koju opisuje točka P čvrsto spojena s bilo kojom krivuljom (ne baš s kružnicom), što se kotrlja bez sklizanja po bilo kojoj drugoj čvrstoj krivulji (ne baš po pravcu), na pr. kružnica po kružnici, → hipocikloida i epicikloida.

LIT.: G. Loria, Spezielle algebraische und transzendente ebene Kurven, II. sv., 2. izd., Leipzig-Berlin 1911. R. C.