AGREGATNO STANJE (lat. aggregare »pridružiti«), u fizici skupljanje čestica nekog tijela u agregatna stanja: kruto, kapljevito i plinovito.

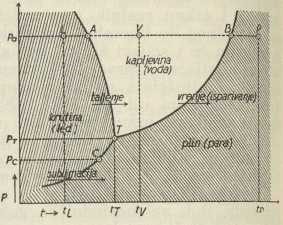
U krutom se stanju tijelo opire velikom silom promjeni i obujma i oblika. U tekućem (kapljevitom i plinovitom) stanju otpor je prema promjeni oblika povoljno malen, ako se promjena vrši dovoljno polagano. Plinovi se od kapljevina razlikuju time, što smanjivanju svog obujma pružaju daleko manji otpor nego kapljevine. Svako tijelo može nastupiti u svakoj od ovih formi, već prema pritisku i temperaturi, pod kojima se nalazi. U p, t-dijagramu (v. sl. 1) mogu se odijeliti područja različitih pritisaka p i temperatura t, koja pripadaju tim agregatnim stanjima. Tako može voda pri atmosferskom tlaku p_a postojati ili kao led L (ako je temperatura t_L < t_A, ili kao voda V (t_A < t_v < t_B), ili kao pregrijana para P (t_P < t_B). Pri atmosferskom je pritisku (760 mm Hg) za vodu t_A = O°C, t_B — 100°C, dok su te vrijednosti za svaki drugi pritisak druge, kako se to razabire iz toka linija taljenja i vrenja. Što je niži pritisak p, to se temperature tališta A i vrelišta B manje razlikuju, da za pritisak p_T obje točke padnu u zajedničku točku T. To je »trojna točka« T (njem. Tripel-Punkt, engl. triple-point). To su naime jedini tlak i jedina temperatura, pri kojima mogu postojati sva tri agregatna stanja nekoga tijela uporedo. Vrijednost trojne točke p_T i t_T za svako su tijelo stalne (fundamentalna točka). Tako je za vodu t_T = + 0,0075°C, p_T = 0,0062 at. Za ugljični dioksid CO₂ je t_T =—56,6°C, p_T = 5,28 at. Kako je za CO₂ tlak u trojnome stanju veći od atmosferskoga, to od okolišnog pritiska mogu postojati sami kruti i plinoviti CO₂, dok se CO₂-kapljevina može promatrati samo u posudama pod pritiskom većim od 5,28 at. Ovo je važno u tehnici hlađenja, jer se kod hlađenja snijegom ugljičnog dioksida ovaj ne tali, već sublimira, i tako ne moči svoj spremnik. Stoga se i kaže: »suhi led« (Trockeneis, dry-ice).

Kruto agregatno stanje može nastupiti u nekoliko oblika. Kod vode je do 10.000 at poznato 5 stabilnih vrsta leda, koje različito kristaliziraju, a koje su stabilne kod različitih pritisaka i temperatura. Tako se dobiva čitav niz trojnih točaka.

Poredak molekula je u svim agregatnim stanjima različit. Kod plinova lete molekule kao taneta slobodno prostorom, dok se ne sraze međusobno ili sa stijenkom suda, da po zakonu sraza promijene smjer i brzinu. Kod krutina atomi titraju (osciliraju) zbog međusobnog utjecaja oko nekog srednjeg položaja. Tek po koji atom ustitra resonancijom tako jako, da se istrgne i poleti dalje, čime dolazi do difuzije i u čvrstim tjelesima (na pr. cementiranje željeza i t. d.). Za kapljevine slika još nije jasna, no čini se, da se molekule giblju nekako između translacije i harmoničnog gibanja (sinusoidalnog titranja), t. j. da se giblju po slomljenom putu, u »cik-caku«. Osim toga su molekule kod kapljevina združene (asocijirane) u veće skupove. Svaka molekula nosi određenu količinu kinetičke energije zbog velike translatorne brzine i zbog eventualne rotacije molekula, a stanovitu potencijalnu energiju zbog molekularnih sila. Zbroj ovih energijica svih molekula čini »unutarnju energiju« U kcal tijela. Kod idealnih je plinova unutarnja energija, a prema tome i specifična toplina ovisna samo o temperaturi, a ne o gustoći. Primijene li se na gibanje ogromnog broja molekula statistička razmatranja s računom vjerojatnosti (kinetička teorija plinova), to se za najjednostavniji slučaj dolazi do istoga rezultata kao s neposrednim pokusom na razrijeđenom plinu, t. j. do jednadžbe stanja t. zv. idealnih plinova PV = GRT ili sa v = V/G do jednadžbe Pv = RT (zakon Boyle-a, Mariotte-a i Gay-Lussaca). Tu je G kg težina plina, T°K apsolutna temperatura u Kelvinovim stupnjevima (v.). V m³ obujam plina, R mkg/kg K individualna konstanta. Što je manja gustoća plina, to se on točnije pokorava ovom zakonu. Kod većih gustoća odstupaju plinovi od idealnih, jer ovdje dolazi do međusobnog utjecaja molekula molekularnim silama koje zbog manjeg razmaka molekula postaju od značaja. Ove sile naime naglo rastu sa smanjivanjem udaljenosti molekula, tako da molekule ne lete više pravocrtno, već po manje ili više zakrivljenim stazama, kad prolijeću međusobno u maloj udaljenosti. To naročito vrijedi za stanja u blizini područja zasićenosti, gdje vrijedi van der Waalsova jednadžba stanja P = Faktor b vodi računa o konačnim dimenzijama molekula, po čemu bi kod obujma v = b molekule bile tako gusto zbijene, da bi se dodirivale, pak se ne bi ni s najvećim pritiskom mogle utisnuti jedne u druge. Član a/v² predstavlja molekularne sile kohezijskog karaktera. Za razdvajanje molekula pri prijelazu u rastresitije stanje troši se energija, tako za taljenje toplina taljenja, za isparivanje toplina isparivanja, za sublimaciju toplina sublimacije. Pri obrnutim procesima iste se topline pri istim temperaturama oslobađaju. Tako je za 1 kg vode

r_isp = 539 kcal/kg pri 1 Atm (100° C) r_tal = 79,5 kcal/kg pri 0° C r_subl = 720 kcal/kg pri —5° C

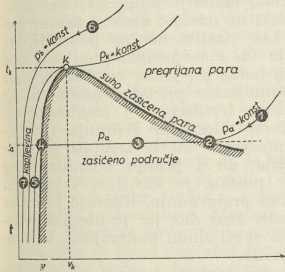
Kritično stanje. Isparivanje i ukapljivanje moguće je samo ispod »kritičnog tlaka i temperature« (Andrews 1869). Plin sa stanjem 1 (v. sl. 2) hladimo pri stalnom tlaku p_a = konst, pa mu temperatura pada do t₂ u stanju 2. U tom trenutku se plin zamagli, t. j. zbog ohlađivanja stvaraju se prve kapljice rose (to je vrelišna temperatura t_a = t₂ = t₃ = t₄ za tlak p_a). Dalje hlađenje (odvođenje topline) ne snizuje temperaturu t_a, već ukapljuje preostali plin tako, da u stanju 4 sve kondenzira (vrela kapljevina 4). Daljim hlađenjem pada opet temperatura, pa je kapljevina u stanju 5 ohlađena primjetljivo ispod svoje vrelišne temperature. Obujam v₂ prvog zamagljivanja (suho zasićena para) bitno je veći od obujma v₄ (vrela kapljevina). Kod visokih pritisaka P_b (P_b > P_k) nema ove promjene obujma u skokovima, već se naprotiv hlađenjem sasvim postepeno, bez zamagljivanja, t. j. bez stvaranja drugog agregatnog stanja, prelazi u stanje 7. Najviši pritisak, do kojega se još može zapaziti zamagljivanje, zove se kritični pritisak p_k s kritičnom temperaturom t_k i kritičnim obujmom v_k.

Tvar	Oznaka	pk kg/cm2	tk °C	vk m3/kg
Živa....	Hg	1000	1470	0,2
Voda....	H2O	225,5	374,1	3,09
Benzol....	C6H6	48,6	288,5	3,3
Alkohol....	C2H6O	65,2	243	3,6
Sumporasta kiselina (anhidr.).	SO2	80,3	157,5	1,92
Amonijak....	NH3	116,0	133	4,24
Ugljični dioksid	CO2	75,3	31,0	2,16
Metan....	CH4	47,3	— 82,9	6,18
Ugljični oksid....	CO	35,8	—139	3,22
Uzduh....	—	38,5	—141	3,2
Vodik....	H2	13,2	—240	32,3
Helij....	He	2,34	—268	15

Postoji veza između promjene obujma i utrošene topline kod prijelaza iz jednog agregatnog stanja u drugo, i to po Clapeyron-Clausius-ovoj jednadžbi

r/T = A (v' −v’) d P/d T

gdje su P i T pritisak i temperatura zasićenja, a jedinični obujmi vrijede: v' m³/kg za polazno stanje (na pr. vrela voda), v" za postignuto stanje (na pr. suho zasićena para), dok je r kcal/kg toplina dovedena za ovaj prijelaz. A =  kcal/mkg je toplotni ekvivalent mehaničkog rada. Kad je kod procesa s dovođenjem topline (r > o) izraz d P/d T > O, onda je v" > v', tako na pr. kod isparivanja vode raste P s temperaturom vrenja t, pa je i obujam pare v" veći od obujma vrele vode v'. Naprotiv je kod taljenja obujam leda v' manji od obujma ledene vode v pa je prema tome d P/d T < O, t. j. kod vode se temperatura ledišta snizuje povišenjem pritiska i to otprilike za 1° pri povišenju pritiska za 100 at.