AEROMEHANIKA je mehanika plinovitog agregatnog stanja. Dijeli se u aerostatiku i aerodinamiku. Prva se bavi pojavama ravnoteže u plinovima pri stalnoj temperaturi, druga pojavama gibanja plinova ili gibanja kroz plin.

U nekim područjima aerostatike možemo plin smatrati tekućinom, koja se od tekućina u užem smislu razlikuje samo svojom stlačivošću. Zato u tim područjima vrijede isti zakoni kao u hidrostatici. Tako zbog vrijednosti Boyleova zakona vrijedi u plinovima Pascalov zakon, koji kaže, da vanjski tlak u tekućinama jednako djeluje u svim smjerovima. Samo kod eksplozija, gdje se val tlaka naglo širi, dolazi do velikih odstupanja od tog zakona, jer se na pojave tlaka nadovezuju nagle zračne struje.

Tlak atmosferskog zraka mjeri se barometrom i jedinicom tlaka (→ barometar).

Za zavisnost tlaka plina o njegovu obujmu pri stalnoj temperaturi (izotermičke promjene) vrijedi zakon, koji je postavio Boyle (1662), a eksperimentalno potvrdio Mariotte (1676). Po tom je zakonu produkt tlaka i obujma plina stalan; t. j. p ∙v = const. Prikažemo li to grafički, uzimajući obujme kao apscise, a tlakove kao ordinate, ta je zavisnost tlaka o obujmu prikazana istostranom hiperbolom, kojoj su koordinatne osi asimptote. Ta se krivulja naziva izotermom. U stvari je Boyleov zakon samo poseban slučaj općeg plinskog zakona p ∙v = nRT za n mola plina u obujmu v (R = plinska konstanta za 1 mol plina, T = apsolutna temperatura), ako temperaturu T držimo konstantnom. Dakle s porastom temperature raste konstanta u Boyleovu zakonu, pa se u grafičkom prikazivanju izoterme s porastom temperature sve to dalje odmiču od ishodišta (sl. 1). Na Boyleovu se zakonu osnivaju zatvoreni manometar, Mac Leodov vakuum-metar, kompresori i običnije sisaljke za tekućine i za plinove (osim molekularne i difuzione). Kako se plin stezanjem zagrijava, a rastezanjem ohlađuje, moraju se izotermičke promjene izvoditi vrlo polako, da bi se temperatura plina prije opažanja tlaka i obujma izjednačila s temperaturom okoline.

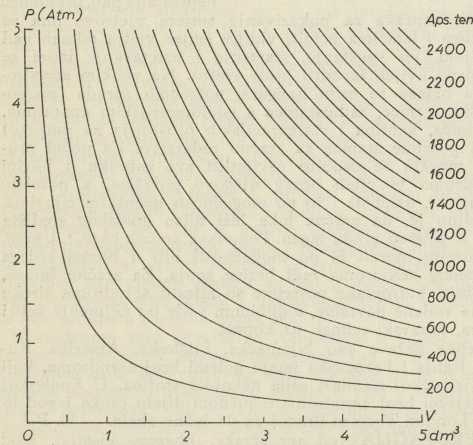
Sl. 1. Izoterme za različite temperature

Boyleov zakon je idealan zakon, kojem se vladanje realnih plinova samo više ili manje približuje, i to tim bolje, što je plin dalje od svoje kritičke točke (→ likvefakcija plinova). Plin, koji bi se u svim područjima tlaka vladao točno po Boyleovu zakonu, zove se idealan plin. Kod zraka, kisika, dušika i još nekih plinova pri sobnoj temperaturi mogu se razlike prema Boyleovu zakonu zanemariti sve do tlakova od 100 atm. Stanju idealnog plina najviše se približuje helij.

Arhimedov zakon o uzgonu vrijedi i u plinovima, pa svako tijelo izgubi u plinu toliko od svoje težine, koliko teži istisnuti plin. Baroskop ili dazimetar (sl. 2) je malena vaga, koja na jednom kraju nosi kovni uteg, a na drugom zataljeni stakleni balon. Vaga je u zraku u ravnoteži. Ova se poremeti, ako aparatić unesemo u lakši ili u teži plin. U lakšem plinu ili u razrijeđenom zraku prevagne krak sa staklenim balonom, u težem plinu krak s kovnim utegom. Svako tijelo izgubi u zraku temperature 0° C i normalnog tlaka 1,293/10s postotaka svoje težine, gdje je s specifička težina tijela. Zato se kod točnih vaganja moraju rezultati svesti na vakuum, da bi se dobile prave mase. Na pr. ako na osjetljivoj vagi u zraku izjednačimo 100 g tvari specifične težine 2,7 s utegom od mesinga specifične težine 8,6, dobivamo za njih nakon redukcije na vakuum znatno nejednake mase (100,048 g za tvar, 100,015 g za uteg), jer su njihovi gubici težine u zraku nejednaki. Na uzgonu u zraku osnivaju se baloni (→ aeronautika) i baloni sonde. Ovi posljednji nose meteorološke sprave ili sprave za mjerenje ionizacije uzduha zbog visinskih zraka, pa su u pojedinim slučajevima doprli više od 30 km visoko (→ visinske zrake).

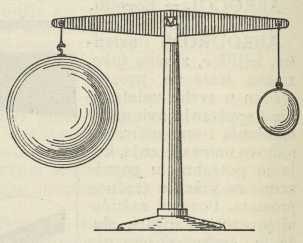
Sl. 2.

Prijelaz između aerostatike i aerodinamike čini istjecanje plina iz jednog rezervoara kroz okrugli otvor pod djelovanjem tlaka, ako je površina otvora malena prema obujmu rezervoara. Tada se brzina, kojom se molekuli u rezervoaru pomiču prema otvoru, može zanemariti. Ako je razlika tlaka p prema vanjskom tlaku p0 malena, izlazi za brzinu istjecanja: <formula> gdje je d masa plina u jedinici obujma. Dakle je kod raznih plinova brzina istjecanja obrnuto razmjerna s kvadratnim korijenom iz gustoće. Primjena formule za veće brzine ograničena je s jedne strane time, što se plinski mlaz izvan suda širi, s druge time, što se kod toga plin ohlađuje. Bunsen je pomoću te formule s dovoljnom točnošću mogao odrediti gustoće nekih plinova.

U aerodinamici možemo u području stacionarnog gibanja plinove smatrati nestlačivim tekućinama, bilo da se tijelo giba u plinu ili da se plin giba, a tijelo miruje. Tako aerodinamika postaje ogrankom hidrodinamike. Struja je stacionarna, ako je brzina u svakoj točci vremenski stalna smjerom i veličinom. Gornja granica za takvo stanje u zraku iznosi 600 do 700 km na sat; kod većih brzina nastaju smetnje od stlačivosti zraka. Prema tome su današnji najbrži avioni dostigli tu graničnu brzinu.

Glavni razvoj aerodinamike nastao je upravo u našem stoljeću u vezi s razvojem aeronautike. To se odrazilo i u pravcu njezina razvoja time, što su glavni napori u istraživanju upravljeni na ispitivanje otpora na tjelesima, koja se gibaju u zraku, sa svrhom, da bi im se dao takav oblik, koji uvjetuje najmanji otpor. Pokazale su se veće poteškoće kod nastojanja, da bi se cijeli kompleks pitanja općenito obuhvatio teoretskim istraživanjem. Načelo sličnosti za slična tjelesa dolazi ovdje slabije do izražaja i u pogledu specifičkog otpora i u pogledu raspodjele otpora po tijelu, koje se istražuje, jer se pokazalo, da kod iste brzine i raspodjela otpora i specifički otpor na pr. na ploči ili na kugli znatno zavise o njihovim dimenzijama. Zbog toga je nova aerodinamika postala čisto eksperimentalnim područjem.

Podloga ovim istraživanjima je načelo relativnog gibanja u aerodinamici, po kome je za pitanje otpora svejedno, da li se tijelo giba u mirnom zraku ili tijelo miruje, a zrak struji suprotnom brzinom. Premda je optok struje drukčiji u prvom nego u drugom slučaju, mjerenja su pokazala, da je taj drugi put, koji je lakše ostvariti za eksperimentalno istraživanje, u prvoj približnosti ekvivalentan prvome. Tako su nastali za potrebe eksperimentalnog istraživanja na što većim modelima t. zv. kanali vjetrova. To je široka cijev glatkih stijena, u kojoj možemo proizvesti široku struju zraka bez vrtloga, a brzinu vjetra mijenjati u širokim granicama. Promjer cijevi u pojedinim slučajevima ide do 16 m, i to ne samo zato, da bi se mogli ispitati što veći modeli, nego i zato, da bi se u srednjem dijelu posve uklonio utjecaj stijene. U sl. 3 je prikazan presjek jednog takvog kanala; brojevi znače metre. U srednjoj cijevi desno je propeler, koji svojim okretanjem stvara struju vjetra. Poprečne pregrade u uglovima su nizovi lopatastih pregrada, koje struju savijaju bez vrtloga. Uklanjanju vrtloga služe i guste mreže kanala u obliku pčelinjeg saća, koje dolaze u izlaznoj cijevi; njihova uloga je i uklanjanje nejednolikosti vjetra. Pogonske snage za propeler idu od nekoliko stotina do nekokoliko hiljada KS, a brzine vjetra do 100 m/sec. Mjerenje ukupnog otpora određuje se zgodno konstruiranim vagama, a za raspodjelu tlaka, koja je u vezi s raspodjelom otpora, upotrebljava se Pitotova cijev u obliku, koji joj je dao Prandtl (pneumometar, sl. 4).

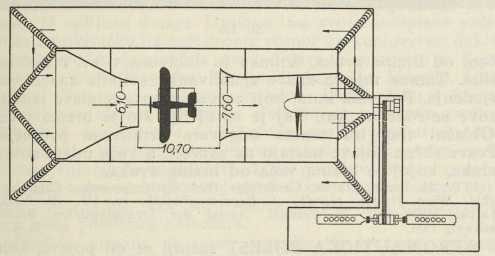
Sl. 3. Horizontalni presjek kanala vjetrova

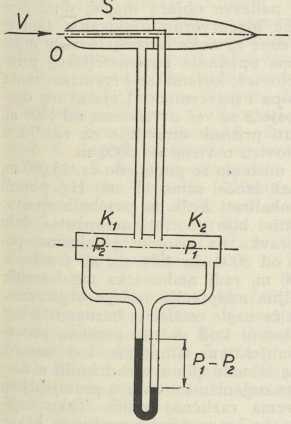
Sl. 4.

Staza, koju u stacionarnoj struji opiše jedna čestica, zove se crtom strujanja. Uzduž nje je zbroj tlaka i kinetičke energije jedinice volumena tekućine u gibanju stalan (Bernouillijev poučak). Crte strujanja u zraku možemo učiniti vidljivima zgodnim dimom (pare titanova tetraklorida) ili lakom prašinom (likopodij). Klasični izraz za otpor glasi; r = K ∙ q ∙ v2, gdje je q površina najšireg presjeka tijela okomito na smjer vjetra, v je relativna brzina, dok bi K trebao biti koeficijent specifičkog otpora, t. j. otpor tijela sličnog onome, koje istražujemo, ali s presjekom q = l m2 kod brzine 1 m/sec. Pokazalo se je, da se otpor daje bolje prikazati izrazom r = K ∙ q ∙ vn, gdje K zavisi i o veličini presjeka tijela i o brzini, dok je općenito n ≷ 2, premda je uvijek blizu 2.

U sl. 5 prikazana je raspodjela crta strujanja oko ravne okrugle ploče, položene okomito na smjer struje. Iza ploče daleko zaobilaze crte strujanja, pa u tom dijelu između ploče i njoj najbližih crta nastaje vrtložno područje, u kom se stvaraju dva vrtloga lijevo i desno od sredine. U savijenim dijelovima crta strujanja nastaju centrifugalne sile, kojih komponenta okomita na ploču proizvodi na ovoj tlak u smjeru struje. Tlak je najveći u sredini ploče. Uopće je tlak upravljen prema konveksnoj strani crta strujanja. Iza ploče je područje podtlaka. Razlika tih dvaju tlakova daje otpor ploče u struji. U sl. 6 su prikazane crte strujanja oko ploče, koja leži koso u struji, pa je posljedica nesimetrije ta, da se ploča nastoji namjestiti okomito u smjer struje. Na tom se osniva Dvořák—Rayleighova pločica za mjerenje tlaka zvuka u akustici.

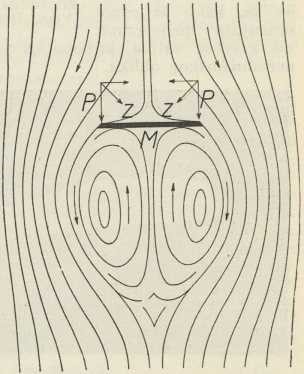
Sl. 5.

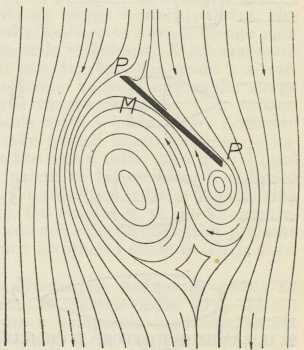
Sl. 6.

Nastavimo li na ploču na strani, okrenutoj izvoru struje, polukuglu, otpor padne na ⅓prijašnje vrijednosti, a pada na ⅙ prijašnje vrijednosti, ako ploču zamijenimo kuglom istog promjera. Upravo kugla je dobar primjer, kako specifički otpor iste kugle zavisi o brzini. U sl. 7 prikazane su crte strujanja oko kugle pri manjoj, u sl. 8 pri većoj brzini. U ovom drugom slučaju je vrtložno područje iza kugle jako umanjeno, pa se tim specifički otpor kugle jako umanjuje.

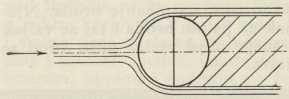
Sl. 7.

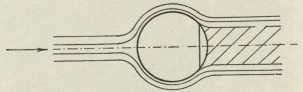
Sl. 8.

Kako velik dio otpora dolazi od vrtložnog prostora iza tijela, otpor će se dalje jako umanjiti, ako glatkoj površini tijela dademo takav oblik, da tijelo u struji ispunja cijeli vrtložni prostor iza svog najšireg presjeka, a ispod ovog presjeka mu površinu tako svedemo, da crte strujanja posvuda teku uza samu površinu tijela. To je t. zv. aerodinamički oblik ili riblji oblik, koji je već davno pronašao Leonardo da Vinci kao oblik najmanjeg otpora, ali je poslije njega pao u zaborav. Tim se oblikom otpor umanjuje na 1/31 prvobitnog otpora okrugle ploče, kojoj je površina jednaka najvećem presjeku aerodinamskog tijela, okomitom na struju. U sl. 9 prikazan je moderni aerodinamski oblik zrakoplova, a u sl. 9a Da Vincijeva crtnja tijela najmanjeg otpora, oboje za isti smjer gibanja (na lijevo). U sl. 10 vidimo tok crta strujanja oko profila avionskog krila. U sl. 11 prikazano je, kako se otpor umanjuje prijelazima od kratkog valjka, kojemu os pada u pravac struje, do aerodinamskog oblika.

Sl. 9.

Sl. 9a. Tijelo najmanjeg otpora po Leonardu da Vinciju (L. da Vinci, Del moto e misura dell' acqua)

Sl. 10.

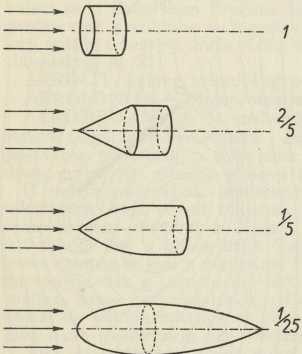
Sl. 11. Zavisnost otpora o obliku tijela (Strelice pokazuju smjer struje zraka)

U sl. 12 vidimo crte strujanja oko dugog valjka, kojemu je os okomita na struju, a koji rotira u smjeru kazala na uri. Iz oblika crta strujanja slijedi prema gornjemu, da na valjak djeluje sila, uperena u smjeru najveće konveksnosti crta strujanja. To je u slici u smjeru drška, koji podržava os valjka. Općenito je u takvu slučaju sila okomita na prvobitni pravac crta strujanja, a uperena je prema onoj strani, na kojoj se smjer rotacije podudara sa smjerom struje. Staza lakog papirnatog valjka, koji rotira padajući, otklanja se na lijevo, ako valjak rotira u smjeru kazala na uri. To je t. zv. Magnusov efekt. Flettner je pokušao tu pojavu praktički primijeniti na gibanje broda. Njegov je rotor bio visok valjak na palubi broda i taj se valjak okretao motorom malene snage. Kad vjetar puše, brod se giba okomito na smjer vjetra.

Sl. 12.

Ako relativna brzina tijela i zraka prelazi spomenutu graničnu brzinu, ne može se zrak, i uopće plin, više promatrati kao nestlačiva tekućina. Tu se javlja utjecaj osnovnog svojstva plina, njegove stlačivosti. To dolazi već kod struja u parnim turbinama i kod gibanja avionskih propelera. Pogotovu to vrijedi za brzine, koje su blizu brzini zvuka u plinu ili je nadilaze. Tu se ne smiju zanemariti ni promjene temperature, koje nastaju zbog naglih promjena obujma plina u blizini tijela. Te pojave čine područje plinske dinamike u užem smislu, a u ovoj čine posebno poglavlje brzine veće od brzine zvuka, kako je to kod puščanog ili topovskog taneta.

Ispred glave tijela, koje se giba velikom brzinom, zrak se naglo zgušćuje, pa se to zgušćivanje širi brzinom zvuka u svim smjerovima. Ali ako je brzina tijela, na pr. taneta, veća od brzine zvuka, val zgušćivanja širi se sporije, nego li nastaju neprestano novi valovi zgušćivanja na glavi taneta. Tu nastaje nešto slično valovima, koji se šire postrance od pramca parobroda, kad se giba na mirnoj vodi. U sl. 13 prikazana je snimka valova zgušćivanja i razrjeđenja oko šiljastog taneta, koje leti kroz zrak brzinom, većom od brzine zvuka. Snimka je dobivena t. zv. metodom šlira. Tamna mjesta znače zgušćivanja, svijetla znače razrjeđenja. Polovina kuta, koji zatvaraju crte iz glave taneta, zove se Machov kut. Taj je to oštriji, što je brzina veća. Oblačni trag iza taneta odgovara vrtložnom području. Posve slične pojave nastaju na zapreci, u koju udara struja zraka, kojoj je brzina veća od brzine zvuka.

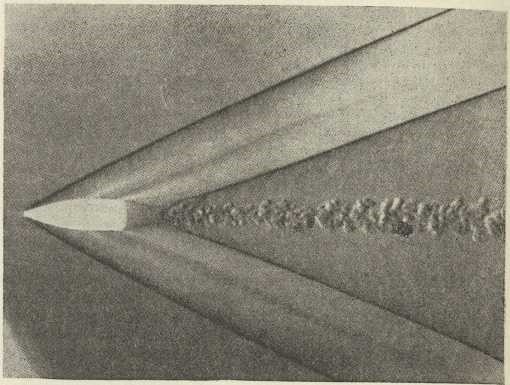
Sl. 13.

LIT.: H. Lamb, Statics, Cambridge 1924; Hydrodynamics, Cambridge 1924; Wien—Harms, Handb. d. Experim.-Physik, sv. IV., dio 1.—3., Leipzig 1930—1932; L. Prandtl, Abriss der Strömungslehre, Braunschweig 1931.