ANALYSIS SITUS ili topologija (češće i geometrija smještaja) jedna je od osnovnih grana matematičkih nauka, koja ulazi u najraznoličnija područja. Razlog mnogovrsnosti njenih primjena jest velika općenitost njena, pa ona, kao još posljednji supstrat matematičkih obilježja, čini osnov razmatranja u područjima, za koja se čini, da su međusobno vrlo daleko. Kad se u razmatranju geometrijskih tvorevina ne obaziremo više ni na metrička svojstva (mjerenje dužina, kutova, površina, obujmova, sukladnost i sl.), ni na projektivna (kad bi bilo svejedno, da li se zrake svjetlosti šire u pravcima ili u kakovim god drugim krivuljama), ostaje još uvijek mnoštvo sasvim određenih svojstava geometrijskih tvorevina, u koja matematička metoda uvodi pregled i vrsta ih u strog sustavizvoda iz početnih nekih pojmova i odnosa i tvori time područje označeno gornjim imenom. Radi velike općenitosti topologije, koja leži u njenoj biti, njena je izgradnjasasvim apstraktna, premda ona izvire iz onoga neoblikovanog (amorfnog) prostora, koji preostaje, kad se iz običnoga geometrijskog euklidskog prostora maknu koordinatni sustavi svake vrsti i bilo kakove sprave za mjerenje, koje su u vezi s pojmom čvrsta tijela, i za koji mislimo, da ga poznajemo iz vlastitoga i pradjedovskog iskustva. Ona istražuje svojstva geometrijskih likova, načinjenih iz plastične građe ili narisanih na rastegljivoj tkanini, koja vrijede i onda, kad likove izobličimo, uz uvjet, da ne dođe do njihova trganja, sljepljivanja ili prekrivanja. Topologija ne čini razlike između dužine, koja spaja dvije točke, i luka krivulje, koja spaja iste točke, između kružnice i elipse, koja iz nje izlazi zgodnom deformacijom ili kružnice i trokuta u nju upisanog. Pritom svakoj točki kružnice pripada samo jedna točka elipse ili trokuta, na koju se točka preslikava, i obrnuto, svakoj točki elipse ili trokuta odgovara samo jedna točka kružnice; osim toga one točke kružnice, koje se zajedno drže, prelaze u točke elipse ili trokuta, što zajedno leže, t. j. pri toj deformaciji ili preslikavanju sačuvana je neprekinutost geometrijskoga lika. Takova preslikavanja uzajmično jednoznačna i uzajmično neprekinuta zovu se topologijska preslikavanja, transformacije ili homeomorfije, a za geometrijske tvorevine, koje tim preslikavanjem izlaze jedna iz druge, kaže se, da su homeomorfne (grč. slično oblikovane) ili topologijski ekvivalentne. Predmet topologije ona su svojstva geometrijskih tvorevina, koja se ne mijenjaju pri topologijskom preslikavanju (invarijantna svojstva). Homeomorfne su dakle tvorevine kugla i elipsoid, kugla i pravilni poliedri u kuglu upisani, na pr. tetraedar, oktaedar. Ali površina kugle kao cjelina nije homeomorfna s površinom kugle, iz koje je izvađena ma i jedna samo točka; širenjem naime otvora, što ga je točka ostavila, može se takva kugla prevesti u polukuglu, a ta rastegnuta u ravninu, u površinu bilo koje kružnice u ravnini i dalje u sav konačni dio obične euklidske ravnine. Za kuglu bez dvije točke slično se razabira, da je homeomorfna s polukuglom bez jedne točke, ili s ravninom kružnice bez jedne točke, a ako se taj otvor proširi, i s kružnim vijencem, u kome izvanja kružnica potječe od deformacije prvog otvora u kugli, a nutarnja od deformacije drugoga kuglina otvora. A kako se kugla s dva otvora može razvući u valjak, kome su ti otvori rubovi osnovaka, ona je homeomorfna i s takovim valjkom. Ali se kugla topologijski bitno razlikuje od površine nazvane torus (prstenasta površina), koja po topologijskom tipu dolazi odmah iza kugle. Ona nastaje rotacijom kružnice oko osovine, koja leži u njenoj ravnini, ali kružnicu ne siječe; na njoj razlikujemo, slično kao na kugli, meridijane i paralele; meridijani su različni položaji kružnice, što se vrti, a paralele su kružnice, što ih opisuje svaka točka zadane kružnice. Razlika između torusa i kugle jest ta, što na kugli svaka zatvorena krivulja bez dvostrukih točaka omeđuje jedan dio kugle i rastavlja je u dva dijela, dok na torusu meridijan ili paralela ne omeđuju dio površine i ne rastavljaju je u dva dijela; istom dva meridijana ili dvije paralele rastavljaju torus u dijelove. Pojam, koji utvrđuje tu osnovnu topologijsku razliku, jest rod p površine, t. j. najveći broj zatvorenih krivulja bez dvostrukih točaka, koje se mogu na površini povući jedna iza druge, da se pri tom površina ne raspadne.
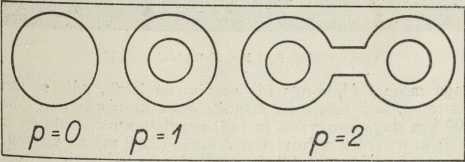 Sl. 1
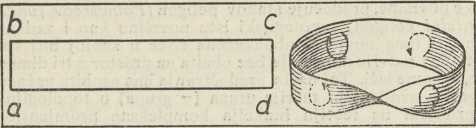
Sl. 1Za kuglu, kao i za elipsoid i za pravilne poliedre, vrijedi p = 0; za torus p = 1; slika prikazuje i zatvorenu površinu s p = 2 (Slika 1.). — Razrežemo li torus duž jednoga meridijana i ispravimo, prelazi on u valjak na oba kraja otvoren, a razrezan još i duž jedne izvodnice toga valjka (koja odgovara paraleli na torusu), prelazi on u pravokutnik; kaže se, da je on jednim parom zatvorenih krivulja kanonički razrezan.Obrnuto, svaki pravokutnik, u kome smatramo po jedan par paralelnih stranica kao lijevi i desni rub jednoga prereza i identificiramo ih, dâ se najprije saviti u valjak, a spojivši dva otvora valjka prelazi on u torus. Isto se prenosi i na zatvorene površine višega roda p; svaka se može s 2p jednostavnih zatvorenih krivulja, koje izlaze iz iste točke površine, razrezati tako, da razvita u ravninu daje poligon s 4p stranica. Ako se uzme u obzir identičnost onih njegovih stranica, koje potječu od lijevoga i desnog ruba istoga prereza, i identičnost onih vrhova njegovih, koji potječu od iste točke površine, predočuje i takov poligon (Poincaréov fundamentalni poligon) topologijski istu površinu kao i zadana, samo je time površina obuhvaćena čišće u svojoj biti kao tvorevina u dvije dimenzije bez obzira na prostor u tri dimenzije, u kome leži. Taj način predočivanja ima osobitu važnost u vezi s uvođenjem teorije grupa (→ grupa) u topologiju i u primjeni na teoriju funkcija kompleksne promjenljive (→ funkcija). Potpun pregled svih površina, koje mogu izaći iz jedne zadane topologijskom deformacijom, daje osnovni teorem, koji kaže, da one i samo one zatvorene dvostrane površine mogu topologijski izaći jedna iz druge, koje imaju isti rod. Rod p dakle ne mijenja se topologijskim preslikavanjem. pa je invarijanta. Dublje se zalazi u topologijsku strukturu površina razmatranjem ciklusa različnih dimenzija. Ciklus dimenzije 0 jest točka, ciklus dimenzije 1 zatvorena jednostavna krivulja, dimenzije 2 zatvorena površina. Za ciklus kojegod dimenzije kaže se, da je homologan nuli, ako omeđuje jedan dio tvorevine, na kojoj leži. Na kugli je svaki ciklus dimenzije 1 homologan nuli, dok ih na toru ima i koji nisu homologni nuli, na pr. meridijan ili paralela. Jedan meridijan i jedna paralela tora primjer su homologno nezavisnih ciklusa dimenzije 1, t. j. takovih, koji zajedno ne omeđuju jedan dio tora, za razliku od dva meridijana ili dvije paralele, koji ciklusi su međusobno homologni i zavisni. Da se uvidi topologijska građa površine, važno je znati najveći mogući broj homologno nezavisnih ciklusa dimenzija 0, 1, 2,... neke tvorevine (Bettijevi brojevi), koji se za zatvorene dvostrane površine ne razlikuju od brojeva suvislosti njihovih S0, S1, S2,... Na zatvorenoj je površini samo jedan nezavisan ciklus dimenzije 0; to je točka, jer dvije točke na takvoj površini možemo uvijek spojiti krivuljom na površini, dakle je nulti broj suvislosti S0 = 1. Za broj suvislosti dimenzije 1 na površini roda p = 0 vrijedi S1 = 0, jer nema zatvorene krivulje, na pr. na kugli, koja bi bila homologno nezavisna; na površini roda p on je 2p; na toru je na pr. S1 = 2. Broj 2p + 1 često se označuje kao suvislost površine. Za broj suvislosti dimenzije 2 vrijedi S2 = 1, jer je sama površina jedini ciklus te dimenzije. Ti brojevi suvislosti (kao i Bettijevi brojevi) zadovoljavaju opću poliedarsku formulu —S0+S1 — S2 = 2p — 2, gdje je broj na desnoj strani Eulerova karakteristika površine, koja je također topologijska invarijanta kao i brojevi suvislosti. Kako ista relacija veže i broj vrhova V, broj bridova B i broj strana S u općim poliedrima, sadržava ona kao specijalan slučaj za p = 0 i elementarnu Eulerovu poliedarsku formulu (za koju je već znao i Descartes): V — B + S = 2 (na pr. za oktaedar, gdje je V = 6, B = 12, S — 8, imamo 6 — 12 + 8 = 2). Topologija razlikuje dakle tvorevine po rodu, a onda po dvostranosti i jednostranosti. Kugla, torus dvostrane su površine s obzirom na euklidski prostor, u kome leže; primjer jednostrane površine je Möbiusova vrpca, koju dobijemo iz pravuktnika abcd (Sl. 2.), kada, držeći čvrsto stranicu ab zakrenemo ravninu pravokutnika za 180° i spojimo stranicu ab s cd tako, da točka a padne u c, a b u d. Ako počevši od jedne točke bojadišemo tu površinu, napredujući uvijek dalje, dok se ne vratimo u početnu točku, i razvijemo je tada u pravokutnik, vidjet ćemo, da su obje strane pravokutnika bojadisane, čime zorno dolazi do izražaja njena jednostranost. Ta je površina obrubljena, jer ima zatvorenih krivulja, koje je omeđuju, slično, kao što je i valjak bez osnovaka ili kugla, iz koje smo izrezali pločicu. Zatvorenu jednostranu površinu dobijemo, kada dva jednaka kruga razrežemo svaki duž jednog polumjera, položimo jedan na drugi i tada najprije rubove zareza spojimo unakrst (lijevi gornji s desnim donjim, lijevi donji s desnim gornjim), a obje obodnice krugova spojimo zalijepivši ih. Kako je kugla najjednostavnija dvostrana površina, tako je i ta t. zv. projektivna ravnina najjednostavnija zatvorena jednostrana površina. Dvostrane površine u euklidskom prostoru daju se orijentirati, t. j. mala kružnica, na kojoj smo označili smisao gibanja kazaljka na uri, ako se pomiče na površini duž kojegod zatvorene jednostavne krivulje, vraća se u ishodište nepromijenjena smisla; jednostrane površine ne dajuse orijentirati, jer ima na njima takovih zatvorenih krivulja, da se nakon završetka puta ista kružnica vratila orijentirana u smislu protivnom od onoga, s kojim je pošla (Sl. 2.). I ta su svojstva topologijske invarijante. I za jednostrane se površine definira rod p (za našu je p = 1). Ako su rod p i broj rubova q (za obrubljene površine) konačni, površina je konačnoga reda suvislosti. Uz zatvorene površine uvode se i otvorene, kao euklidska ravnina ili hiperboloid, isto tako i površine beskonačnoga reda suvislosti. Topologija daje potpun pregled svih mogućih topologijskih tipova u dvije dimenzije, dok ni izdaleka nemamo toga u tri dimenzije.
 Sl. 2
Sl. 2Dva se smjera ističu u izučavanju topologije; jedno je kombinatorna ili algebarska topologija, u kojoj se proučavanje geometrijskih tvorevina svodi na jednostavnije građene, na simplekse: točke, dužine, trokute, tetraedre i slično u višim dimenzijama, iz kojih se sastavljaju kompleksi u obliku vrlo općih poliedara različnih dimenzija, koji su predstavnici osobito važna pojma raznoličnosti (v.) u različnim dimenzijama, a koji sadržava i pojmove krivulje, površine i trodimenzionalnih tvorevina. Za opis građe kompleksa uvodi se i simboličko označivanje, koje vodi dalje i do uvođenja algebarskih metoda, kao što je prvi općeno učinio H. Poincaré. Drugi se smjer osniva na teoriji skupova (→ skup); s pomoću pojma susjedstva u zadanom nekom skupu i aksiomâ, koje on zadovoljava, uvodi se pojam neprekinutosti i topologijskoga preslikavanja te topologijskoga prostora, a zatim i raznoličnosti. Broj dimenzija raznoličnosti uvodi se kao topologijska invarijanta; on je u vezi s jednim od najvažnijih teorema topologije o nepromjenljivosti dimenzija (Brouwer 1911), po kome je nemoguće, da se tvorevina jedne dimenzije topologijski preslika na tvorevinu sa više dimenzija; ako su dakle dvije tvorevine homeomorfne, one su i jednakih dimenzija. Jedan od prvih rezultata toga smjera bio je teorem Jordanov, da svaka zatvorena krivulja bez dvostrukih točaka dijeli ravninu u dva područja. Danas je tendencija u topologiji, da se ta dva smjera usklade.
I pitanja smještaja geometrijskih tvorevina čine važno područje topologije, puno teškoća i nerješivih problema. Ovamo pripada t. zv. problem zauzlanosti krivulja, na pr. pitanje, da li je krivulja smještena u prostoru kao kružnica ili se provlači kroz svoje zavoje i zauzlava, ili i pitanje, da li dvije krivulje zahvataju jedna u drugu kao karike lanca ili su jedna izvan druge.
Prva istraživanja topologijske naravi potječu iz 18. st.; to je problem sedam mostova u gradu Königsbergu, koje treba prijeći jednim potezom (Euler), zatim poliedarski teorem Eulerov. S Eulerovim je problemom srodan i problem igre domino, kao i traženje izlaza iz bilo kakova labirinta, jer su sve to problemi kompleksa dužina. No od Riemannova uvođenja topologijskih razmatranja u teoriju algebarskih funkcija koja je time iz apstraktnoga dotadašnjeg oblika dobila jasan i zoran geometrijski oblik, pa od osnovnih misli Poincaréovih datira današnja topologija, koja obuhvata izvanredno različna područja, jer se pod točkama njenih raznoličnosti mogu razumijevati najrazličniji matematički predmeti, na pr. stanja mehaničkih sustava.
LIT.: O. Veblen, Analysis situs, 2. izd., New York 1931; H. Weyl Die Idee der Riemannschen Fläche, 2. izd., Berlin 1923; E. Cartan, Leçons sur la Géométrie des espaces de Riemann, Pariz 1928; H. Seifert, W. Threlfall, Lehrbuch der Topologie, Leipzig-Berlin 1934; P. Alexandroff, H. Hopf, Topologie, Berlin 1935. Ž. M.