 Sl. 1.
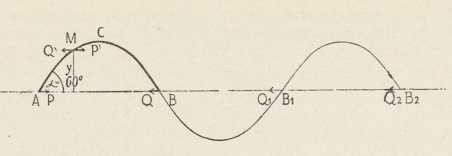
Sl. 1.ELASTIKA (lat. elastica) ili elastička krivulja nastaje, kad se kruta elastična vrpca (tanak štap), izprva ravna, svine u krivulju AMB (sl. 1) silama P i Q, koje djeluju na krajeve vrpce. Uvjet je ravnotežja, da su sile jednake i protivne, Q = —P, i da su u istom pravcu, a krajevi mogu biti na pr. svezani užetom tako, da sile nastaju od napeta užeta. Da se nađe zakon te krivulje, treba izpitati ravnotežje diela vrpce, koji seže od kraja A do koje god točke M. Na taj komad osim sile P djeluju još i sile, što ih preostali dio vrpce, MB, izvodi na AM kroz prorez vrpce na mjestu M. Te sile nalazimo tako, da u misli premjestimo silu P na kraj M komada AM; u tu se svrhu dodaju kod M dvie jednake i protivne sile P' i Q', gdje je Q'=—P' = -P. Sila P se time nadomješta silom P' i parom sila P i Q'. Taj par sila ima momenat U = P ∙ y, ako je y udaljenost točke M od pravca sila AB. Sile, koje djeluju kroz prorez, moraju biti dakle takve, da su u ravnotežju sa silom P' i sa spomenutim momentom. Ako se vrpca u misli razstavi u uzporedna vlakna, bit će ova radi svinutosti vrpce na unutarnjoj strani krivulje stisnuta, a na izvanjoj nategnuta, pa kroz prorez M djeluju i tlakovi i vlakovi. Zbroj momenata S svih tih sila zove se moment savijanja. On je to veći, što je veća krivost vrpce x (= l:r, ako je r polumjer krivosti), te je S = b ∙ ϰ, gdje se faktor b zove krutost u savijanju. Moment S u ravnotežju je s momentom U, što daje osnovno svojstvo e-e
b ∙ ϰ = —P ∙ y. (1)
Po tom je zakonu krivost u kojoj god točki e-e razmjerna udaljenosti točke od pravca izvanjih sila. U krajnjim je točkama A i B krivost dakle = 0. Uostalom u tim točkama krivulja geometrijski ne prestaje, već se nastavlja u jednakim lukovima BB1, B1B2,... na jednu i drugu stranu u bezkrajnost. Kako u točkama A, B, B1, B2,... krivost mienja predznak, te točke zovemo točkama infleksije. Fizikalno to znači, da bi umjesto vrpce AB mogli uzeti vrpcu na pr. dvostruke dužine, koja bi se mogla svinuti u oblik AMBM1B1 silom P u točki A i silom Q1 (=—P) u točki B1. Tako se mogu zamisliti e-e, koje između krajnjih točaka imaju jednu ili više točaka infleksije. Međutim bi ravnotežje takve vrpce bilo labilno, t. j. nemoguće, te bi ga već najneznatniji poticaj pokvario.
Za bliže iztraživanje e-e uvodi se dužina s njezina luka i kut Θ, što ga čini tangenta krivulje s pravcem sila. S obzirom na to, da je ϰ = d Θ : ds, sliedi iz (1) diferencialna jednačba e-e
b/p · d2Θ/ds2 = — sin Θ. (2)
Ta se jednačba podudara s jednačbom gibanja (sastavljena) njihala, gdje također Θ znači kut, i to kut, koji čini težištnica okomita na osi njihala s vertikalom, dok s znači vrieme. Krivosti e-e odgovara kod njihala kutna brzina. Što je kod e-e njezin početak, točka A, gdje je Θ = α, ϰ = 0, to je kod njihala mjesto najveće elongacije, gdje je kutna brzina 0. Najveću krivost ima e. u C, gdje se najviše udaljila od pravca sila; kod njihala je tomu analogija čas, kad ono prolazi kroz položaj ravnotežja, te mu je brzina najveća.
Zadaću e-e načeo je Jakob (I.) Bernoulli, potanko razmotrio moguće slučajeve Euler 1744, dok podpuno njezino rješenje iziskuje primjenu eliptičkih funkcija.
 Sl. 2.
Sl. 2.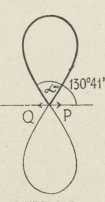 Sl. 3.
Sl. 3.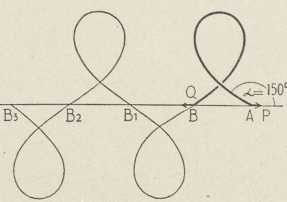 Sl. 4.
Sl. 4.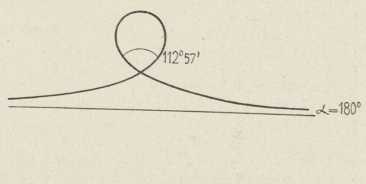 Sl. 5.
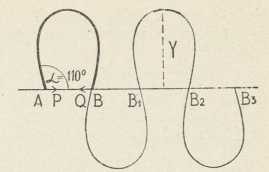
Sl. 5.Različiti se oblici e-e dobivaju, kad se mienja razmak njezinih točaka infleksije. Da se krajnje točke A i B zbliže i pri tom ne mienjaju sile P i Q, treba uzeti primjereno dulji komad vrpce. Kut α, što ga početak vrpce čini s pravcem sila, postaje onda veći. Tako kutu α = 110º pripada krivulja sl. 2. Ako je α = 130º41' (Euler), krajnje se točke A i B sastaju (sl. 3), lukovi se e-e poklapaju i čine oblik osmice. Sile P i Q izobliče još dužu vrpcu toliko, da se krajevi mimoilaze (sl. 4). Za α = 180º e. se sastoji samo od jednoga, bezkrajnog luka, koji se pravcu sila približuje asimptotički (sl. 5). Već je Euler napisao jednačbu te krivulje i našao, kolik joj je kut u petlji (112º56'48"), i kolika je udaljenost krivuljine dvotočke od pravca sila. Kod njihala tomu odgovara slučaj, kad njihanje započne iz namještaja, gdje je njihalo »izvrnuto« i u labilnom raznotežju, te je vrieme 1 njihaja ∞.
Ako se najveći razmak točaka e-e od pravca sila označi sa Y (sl. 2), vriedi za primjere, koji su dosada spomenuti,
Y = 2
sin
. (3)
 Sl. 6.
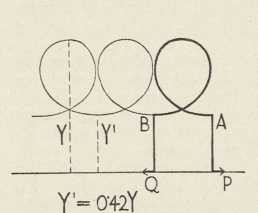
Sl. 6.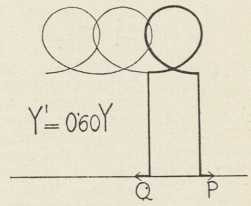 Sl. 7.
Sl. 7.Preostaju oni oblici e-e, koji odgovaraju gibanju njihala, kod kojega uobće nema njihanja, već se njihalo vrti vazda u istom smislu. E. sada nema točaka infleksije te je svagdje svinuta u istom smislu (sl. 6 i 7). Udaljenost se od pravca sila sada mienja između najmanje vriednosti Y', u točkama A i B, i najveće vriednosti Y. Sile P i Q mogu držati komad AB u njegovu izobličenju na taj način, da se u A i B na e-u pričvrste po jedan komad savršeno krute tvari, koja seže do pravca sila. To vriedi, kao da bi sila P djelovala u A, Q u B, i kao da bi povrh toga u svakoj od tih točaka djelovao još i par sila (bez kojega u A i B ne bi bilo krivosti). Za ove primjere vriedi
Y2 — Y'2 = 4 ∙
. (4)
Bezkrajno dugi luk (sl. 5) jest granični slučaj za ovu jednačbu kao i za (3). Treba u (4) staviti Y' = 0 ili u (3) α = 180º, da se dobije visina bezkrajno duga luka Y=2
.
Već je Euler tim primjerima dodao još i e-u, koja je kružnica. Njezina je analogija gibanje njihala, kojemu je težište u osi, te ono postaje zamašnjak, koji se vrti stalnom brzinom. Jednačba e-e (1) tad glasi: b ∙ ϰ = konst. Tomu treba da je P ∙ y stalno, što se teoretski obuhvaća pomišlju, da sila P postaje sve manja, a njezino hvatište prelazi u bezkrajnost, i to tako, da je lim(P ∙ y) = konst.
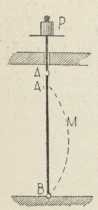 Sl. 8. Ako je P veće od
Sl. 8. Ako je P veće od
»tereta izvijanja«, štap AB klone
i dobije oblik Elastike A1 MBNa iztraživanje e-e nadovezuje se Eulerovo, tehnički važno odkriće formule za izvijanje (izgib, njem. Knickung). Vertikalnom štapu, koji se svršava u kugličnim zglobovima, donji je kraj, B (sl. 8), učvršćen, dok se gornji, A, može pomicati u vertikali. Ako se štap odozgo obtereti utezom P, pod kojim se ne će smrviti, može se dogoditi jedno od dvoga: ili štap ostane ravan, pa se čak i vrati u svoj ravni oblik, ako smo mu načinili izbočinu i opet ga pustili; ili se štap izvine i primi oblik e-e. U potonjem je slučaju ravni oblik štapa bio oblik labilnoga ravnotežja, te je utezom P prekoračena granica štapove čvrstoće prema izvijanju. Ta se čvrstoća izražava najmanjim teretom P0, koji stvara izvijanje. Da se nađe P0, treba imati na umu, da za maleno α e. ima oblik sinusoide, s lukom, koji je jednak dužini l štapa, i amplitudom Y. Ako je l' razmak krajnjih točaka izvinutoga štapa, krivost je sinusoide na mjestu najveće krivosti —
Y, pa je prema (1) b ∙
= P,
iz čega sliedi glasovita »Eulerova formula«
P0 =
. Čvrstoća je prema izvijanju dakle to veća, što je veća krutost u savijanju b, i ona je obrnuto razmjerna kvadratu dužine štapa; štap dvostruke dužine klonut će već pod četvrtinom tereta.
Jednostavan je put do Eulerove formule i ovaj. Luk sinusoidnc e-e ima dužinu π
(analogno vremenu njihaja, kada je amplituda malena), i ta dužina ne može biti veća od l, te se P0, dobiva iz jednačbe
Veličina b zavisi o tom, kako je ravnina, u koju se štap savija, smještena prema prorezu štapa. Ima doduše primjera, gdje za sve te ravnine vriedi isto b (na pr. prorez krug), ali ako je prorez na pr. plosnat pravokutnik (primjer vrpce), onda je b manje, kada je ravnina savijanja uzporedna debljini proreza, veće, kada je uzporedna širini. Za čvrstoću prema izvijanju odlučna je, dakako, najmanja vriednost b.
LIT.: Ostwalds Klassiker der exakten Wissenschaften, Br. 175. (Jak. Bernoulli, Euler), Leipzig 1910.St. H.