DVOSTRUČENJE KOCKE (duplicatio cubi, delski problem) čini sa trisekcijom kuta i kvadraturom kruga tri t. zv. klasična problema geometrije, koji su, niknuvši na tlu stare grčke geometrije, bitno utjecali na njezin razvoj. Zbog njih su grčki geometri pronašli različite krivulje (čunosječnice, cisoidu, konhoidu, kvadratrisu i t. d.), a s ovima u svezi načeli opet druga matematička područja.
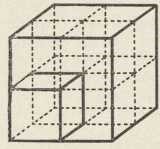 Sl. 1.
Sl. 1.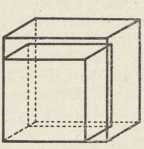 Sl. 2.
Sl. 2.Podrietlo problema podvostručenja kocke obavito je legendama, za koje znamo iz jednog pisma grčkoga geometra Eratostena (276—194) upravljenoga egipatskom kralju Ptolemeju II. (vladao 247—222). Prva od njih priča, da u jednoj, po svoj prilici Euripidovoj tragediji, mitoložki kretski kralj Mino (prije 1100 pr. Kr.), vidjevši, da su za njegova sina Glauka načinili grobnicu u obliku kocke premalenom, nalaže graditelju, da ovu podvostruči, i to tako, da podvostruči brid kocke, dok su po drugoj oko g. 400 pr. Kr. stanovnici otoka Dela (zato: delski problem) prema savjetu delfskog proročišta trebali podvostručiti jedan kockasti oltar, da bi se oslobodili kuge, koja je tada harala po otoku. Jasno je, da odredba Minova ne znači rješenje problema, jer se podvostručenjem brida obujam kocke poosmerostručuje (sl. 1, izpravni odnošaj dviju kocaka prikazan je u sl. 2); to je dakako bilo poznato i starim grčkim matematičarima, te i sam Eratosten iztiče tu neizpravnost. Deljani su pak, po Eratostenu, nalazeći se u velikoj neprilici, poslali svoje poslanike geometrima iz Platonove akademije s molbom, da nađu rješenje zadatka. No već prije toga sveo je Hipokrat s Hija (oko 440 pr. Kr.) problem d-a k-e na jedan drugi, naime na određivanje dviju srednjih proporcionala za dvie zadane dužine, čime se — veli Eratosten — neprilika nije ništa umanjila. Geometri pak iz Platonove škole dali su se na posao, da rieše taj drugi problem, te je tako Platonov prijatelj Arhita iz Tarenta (430—365) dao rješenje s pomoću presjeka valjka, stožca i svitka (torusa), učenik Platona i Arhite Eudokso sa Knida (408 do 355) s pomoću nekih nama nepoznatih crta, a učenik Platonov Menehmo (oko 350 pr. Kr.) s pomoću čunosječnica, koje je upravo i pronašao kod rješavanja toga zadatka.
Ako su zadane dvie dužine a i b, a tražene dvie srednje proporcionale njihove x i y, dakle:
a : x = x : y = y : b, (1)
tada odatle sliedi:
x3 = a2b,
a za b = 2a imamo:
x3 = 2a3, (2)
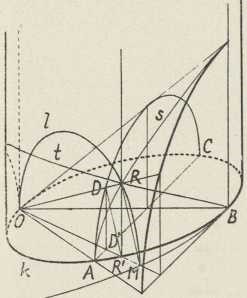 Sl. 3.
Sl. 3.t. j. dužina x doista je brid kocke, koja ima dva puta veći obujam od kocke s bridom a. Nije dakle 2a brid tražene kocke, nego je to manja od dviju srednjih proporcionala za brid a zadane kocke i njegova dvokratnika 2a. Međutim, ta se srednja proporcionala x ne da konstruirati elementarno, t. j. s pomoću ravnala i šestara, jer jednačba (2) nije reduktivna, ali je Hipokratova zasluga u tome, što je prostorni problem sveo na jedan zadatak u ravnini, koji se ipak dade lakše iztraživati. Ako se dakle gdje govori o rješenju problema d-a k-e na temelju jednačbe (2), tada je ono ili neelementarno, t. j. izvedeno s pomoću pravaca i kružnica i povrh toga još nekih drugih linija, ili je elementarno, ali onda nuždno aproksimativno, t. j. daje samo približni rezultat. Od neelementarnih rješenja prvo je dao Arhita: ono je izvanredno oštroumno i sasvim svoje vrsti, jer rješava jednačbu (2) s pomoću prostornih tvorevina, što nijedno drugo rješenje ne čini. Ako u kružnicu k s promjerom OB = b unesemo tetivu OA = a (sl. 3), tada će rotacioni stožac, koji se dobije vrteći pravac OA oko pravca OB, sjeći uzpravni valjak nad kružnicom k kao osnovkom u nekoj krivulji s. Položimo li pak pravcem OB ravninu okomito na ravninu kružnice k, u njoj konstruiramo kružnicu nad dužinom OB kao promjerom, te ovu kružnicu rotiramo oko njezine tangente u točki O, tada će ona opisati plohu, koja se zove zatvoreni torus ili svitak (v.). Ta ploha sieče onaj valjak u nekoj krivulji t, a ova opet krivulju s u točki R, koja rješava naš problem. Ponajprije, ta je točka zajednička svima trima plohama: valjku, stožcu i svitku, i zato leži na izvodnici RR' valjka, odnosno izvodnici OR stožca, te na meridianu l ≡ ORM svitka (ove tri crte leže u jednoj istoj ravnini, naime ravnini meridiana). Ako zatim točkom A položimo ravninu okomito na os OB stožca, sjeći će ona stožac u kružnici, kojoj je AC promjer u ravnini kružnice k, a D joj je sjecište s izvodnicom OR. Jasno je, da normalna projekcija D' točke D na ravninu kružnice k pada u sjecište pravaca OR' i AC, pak iz pravokutnoga trokuta ACD sliedi: DD'2 = AD' ∙ D'C. No iz kružnice k sliedi po stavku o odsječcima na sekantama: AD' ∙ D'C = OD' ∙ D'R', te je tako DD'2 = OD' ∙ D'R', a to znači, da je trokut ODR' pravokutan u vrhu D. Kako su pak trokuti ORR' i OMR očigledno pravokutni (u vrhu R' odnosno R), a imaju oštar kut kod O zajednički i među sobom i s trokutom ODR', sliedi, da su ta tri trokuta među sobom slična, dakle je OD : OR' = OR' : OR = OR : OM. Uzmemo li sada u obzir, da je OD = OA = a, OM = OB = b, te uvedemo oznaku OR' = x, OR = y, imamo tako:
a : x = x : y = y : b,
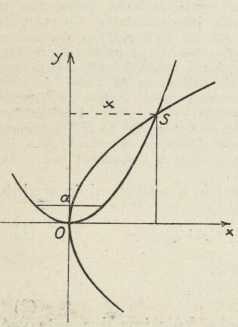 Sl. 4.
Sl. 4.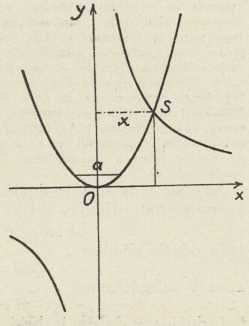 Sl. 5.
Sl. 5.a to je upravo naša relacija (1). — Ovo je rješenje važno po tome, što je to prvi slučaj prostornog rješavanja jednog planimetrijskog problema u starogrčkoj matematici; a s druge se strane moramo diviti autoru toga rješenja, jer ono predpostavlja jedno duboko i za ono doba obsežno poznavanje geometrije te izvanredno jako razvito prostorno zrenje. — Menehmo rješava jednačbu (2) na dva načina: najprije s pomoću dvie parabole, koje imaju zajedničko tjeme, osi su im među sobom okomite, a parametri su im a i 2a (sl. 4), dakle njihove jednačbe glase x2 = ay i y2 = 2ax, odakle izlazi za abscisu x njihova sjecišta S x3 = 2a3, a to je upravo naša jednačba (2). Dakako, da su jednačbe tih dviju parabola dobivene iz temeljne relacije (1), ako u ovu stavimo b = 2a. No iz ove sliede još i ove dvie jednačbe: xy = 2a2 i x2 = ay, koje geometrijski znače jednu istostraničnu hiperbolu i jednu od one dvie parabole (sl. 5), a abscisa x sjecišta S tih dviju krivulja opet je dana jednačbom (2). Dakako da Menehmo nije za svoje izvođenje imao na razpolaganje ovaj netom izneseni analitički aparat, nego je prema tadašnjem stanju grčke matematike sve te analitičke operacije izvodio u geometrijskom obliku — način, kojemu se moramo danas diviti, makar nam se s našeg sadašnjeg stajališta čini tako jednostavan. — Druga dva grčka geometra (živjeli su oko 180 pr. Kr.) pronašla su za rješenje jednačbe (2) druge krivulje, i to Dioklo krivulju 3. reda cisoidu (v.), a Nikomed krivulju 4. reda konhoidu (v.). U novom vieku dali su najvažnija rješenja jednačbe (2) R. Descartes (1596—1650) u svojoj slavnoj Géométrie (1637), Gregorius a St. Vincentio (1584—1667) u djelu Opus geometricum (1647) te R. F. Sluse (1622—1685) u djelu Mesolabium (1668); sva trojica temelje svoje rješenje opet na čunosječnicama (kao Menehmo), a Sluse kao jedini na elipsi. V. Viviani (1622— 1703) je dao rješenje s pomoću krivulje 3. reda xy2 = a3.
Važnija elementarna i zato aproksimativna rješenja dali su tek u novije doba L. Mascheroni (1797), G. Buonafalce (1876), G. I. Vargiù (1877) te G. Boccali (1884). Međutim, rješenja ove vrsti ima izvanredno velik broj (i iz najnovijih dana), samo što nisu sva jednako vriedna po stupnju svoje približnosti, odnosno točnosti.
Napokon još treba spomenuti mehanička rješenja d-a k-e, t. j. rješenja s pomoću neke sprave, aparata ili mehanizma. Prvi je dao takvu spravu (i uobće prvu za rješavanje nekoga geometrijskog zadatka) Platon (427—347), premda je inače bio odlučan protivnik neeksaktnog rješavanja geometrijskih problema, t. j. rješavanja, koje se ne služi samo ravnalom i šestarom; zatim je dao Eratosten spravu, koju je Papo (oko 300 posl. Kr.) nazvao mezolabij, a u novije doba Descartes jedan mehanizam u svojoj Géométrie. Ovamo se moraju svrstati i rješenja, koja se temelje na uklapanju neke dužine između dvie linije, kako su ih dali Apolonije iz Aleksandrije (oko 200 pr. Kr.), Heron iz Aleksandrije (oko 100 pr. Kr.) te Filon iz Gadare (u 1. st. pr. Kr.). Ta rješenja naime ne možemo smatrati aproksimativnima u teoretskom smislu, jer se sastoje u pokušavanju, i ne da im se izračunati granica točnosti odnosno stupanj aproksimacije. Ono uklapanje izvodi se naime s pomoću ravnala, ali ovo pri tom služi ne kao redovito, t. j. za crtanje pravca po volji, odnosno kroz jednu ili dvie zadane točke, nego mu je služba sada posve nova, upravo zbog toga, što su na njemu sada markirane dvie točke (krajnje točke dužine, koja se ima uklopiti), koje moraju pasti na zadane dvie linije, a da brid ravnala pri tom ide nekom zadanom točkom.
LIT.: F. Enriques, Fragen der Elementargeometrie, II. dio (na njem. izdao H. Fleischer), Leipzig 1907; A. Herrmann, Das Delische Problem, Leipzig-Berlin 1927.R. C.