ČUNOSJEČNICE (sjekotine stošca, konike). Za te krivulje postoje različite definicije, od kojih ćemo navesti najglavnije vremenskim redom, čime ćemo ujedno označiti najvažnije povijesne momente iz razvoja nauke o čunosječnicama.
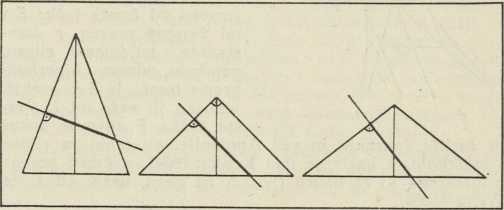 Sl. 1.
Sl. 1.1. Grčki geometar Menehmo (oko 350 pr. Kr.), za koga se općenito drži, da je pronašao čunosječnice u svrhu rješavanja t. zv. delskog problema (v.), poznaje tri vrsti tih krivulja, i to kao presjeke rotacionog čunja (v.) ili stošca s nekom ravninom, koja je okomita na jednoj izvodnici stošca. To su t. zv. presjek oštrokutnog, pravokutnog i kosokutnog stošca, gdje se ovi nazivi odnose na kut, što ga ima osni presjek stošca na vrhu dakle na t. zv. otvor stošca. U sl. 1. predočena su ta tri stošca s pomoću svojih osnih presjeka (dakle »u profilu«), a pripadni presjeci jače izvučenom dužinom. To su zapravo elipsa, parabola i hiperbola, ali ti nazivi još ne dolaze kod Menehma. Skupno ime »čunosječnice« odgovara njihovu postanju.
2. Apolonije iz Perge (v.), koji je napisao izvanredno važno i sjajno djelo o čunosječnicama u 8 knjiga, definira na početku toga djela te krivulje isto tako prostorno, t. j. kao presjeke stošca i ravnine, ali je napredak prema Menehmu najprije u tome, što se ne ograničuje na rotacioni stožac, nego radi i s kosim kružnim stošcem, a onda u tome, što kod hiperboličnog presjeka uzima potpun stožac tako, da dobiva obadvije grane krivulje, a ne samo jednu kao Menehmo. No još je važnija treća novost kod Apolonija, koja se sastoji u tome, što on te krivulje s pomoću njihova prostornog postanja definira i planimetrijski, t. j. kao krivulje u ravnini. Pri tom pak dolazi za svaku od tih krivulja do izvjesne jednadžbe (danas te jednadžbe zovemo tjemenim jednadžbama), u kojoj se javlja na desnoj strani izvjesni nedostatak (ἔλλειψις), jednakost (παραβολή), odnosno pretičak (ὑπερβολή), a po ovima su onda te krivulje dobile svoja imena, koja su im trajno ostala. U današnjem našem pisanju glase te jednadžbe po redu:
y2=2px—qx2, y2=2px, y2=2px+qx2,
te odgovaraju sl. 2, 3, 4. Tu su p i q posve određene veličine, koje potječu od smještaja dotične čunosječnice na stošcu, ili točnije, od smještaja presječne ravnine prema stošcu. Prva jednadžba veli, da kvadratu sa stranicom y=QE nedostaje pravokutnik sa stranicama x= OQ i qx, pa da bude jednak pravokutniku sa stranicama x= OQ i 2p; druga veli, da je kvadrat sa stranicom y= OP upravo jednak ovom pravokutniku, a treća, da kvadrat sa stranicom y= QH premašuje taj pravokutnik za pravokutnik sa stranicama x= OQ i qx. Veličina 2p zove se parametar (Mydorge 1631) ili latus rectum, a veličina 2p q latus transversum (kod elipse je to velika, kod hiperbole glavna os); ova su dva posljednja tehnička naziva latinski prijevod odnosnih naziva, koje ima već Apolonije.
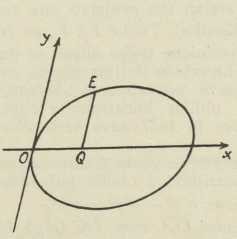 Sl. 2.
Sl. 2.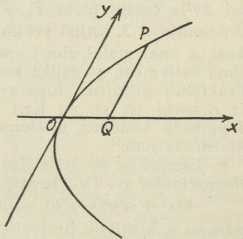 Sl. 3.
Sl. 3.3. Grčki geometar Papo iz Aleksandrije (oko 300 pos. Kr.) u VII. knjizi svoga djela Συναγωγή ili Collectiones (»Zbirka«, koja u 8 knj. sadržava izvadke i komentare glavnih tadanjih matematičkih djela) daje ovu definiciju: čunosječnica je geometrijsko mjesto točaka, od kojih svaka ima to svojstvo, da je omjer k njezinih udaljenosti od čvrste točke F i od čvrstog pravca r konstantan, te imamo elipsu, parabolu, odnosno hiperbolu prema tome, je li k manje, jednako ili veće od 1. Čvrsta točka F zove se fokus ili žarište (poznaje ju već Apolonije, ali samo za elipsu i hiperbolu, a naziv je dao Kepler 1604), a čvrsti pravac r direktrisa ili ravnalica (pojam od Papa, naziv od J. de Witta 1658).
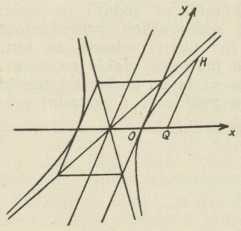 Sl. 4.
Sl. 4.Ovu je definiciju Ruđer Bošković u djelu Sectionum conicarum elementa, izašlom g. 1754. u Rimu kao III. svezak skupnoga djela Elementa universae Matheseos, uzeo kao ishodište čitave svoje teorije tih krivulja, te je ovu izveo i proveo dosljedno na način Apolonijev (t. j. bez sredstava analitičke geometrije, dakle čisto geometrijski). Pri tom je (u §-u 140) uveo pojam (kasnije tako nazvane) generacione kružnice. Ovo Boškovićevo djelo o čunosječnicama treba smatrati zaključnim i najdotjeranijim djelom u nizu sintetičkih, t. j. čisto geometrijskih obrađivanja tih krivulja, dok je Eulerovo djelo Introductio in Analysin infinitorum (izašlo 1748), u svom II. svesku, prva sustavna obradba čunosječnica s pomoću metoda analitičke geometrije.
4. Francuski matematičar G. Desargues razvio je u djelu Brouillon project d’une atteinte aux événemens des rencontres d’un cone avec un plan (Pariz 1639) teoriju čunosječnica kao centralnih projekcija kružnice. Dakle se zapravo vraća na staru Apolonijevu definiciju tih krivulja (ravni presjeci kružnog stošca). No Desarguesovo djelo znači izvanredno važan napredak u razvoju nauke o čunosječnicama zbog općenitosti svojih shvaćanja i važnosti rezultata. Od osobite je važnosti to, što je D. uveo u geometrijska razmatranja pojam neizmjerno daleke točke (ali ne neizmjerno dalekog pravca!).
5. Francuz Ph. de la Hire u djelu Nouveaux élémens des sections coniques (Pariz 1679) uzima kao prvi na čelo svoje teorije čunosječnica definiciju, po kojoj je elipsa (odnosno hiperbola) geometrijsko mjesto točaka, od kojih svaka ima to svojstvo, da je zbroj (razlika) njezinih udaljenosti od dvije čvrste točke F1, F2 stalan (to svojstvo zna već Apolonije u 3. knjizi svojih Konika). Točke F1, F2, su fokusi, a onaj stalni zbroj »provodnica« točke elipse je duljina velike osi, a razlika kod hiperbole duljina glavne osi. Praktičnu primjenu toga svojstva poznaje već Antemije iz Bizanta (6. st. po Kr.) u obliku konstrukcije elipse s pomoću konopca, a Descartes ju 1637 zove vrtlarskom konstrukcijom.
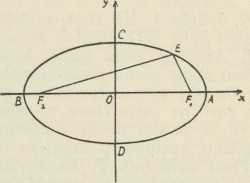 Sl. 5.
Sl. 5.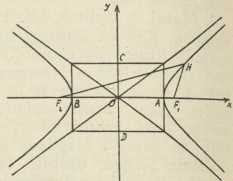 Sl. 6.
Sl. 6.F. Lacroix je tu definiciju g. 1798 u djelu Cours de mathématiques, sv. IV., izrazio analitički u obliku jednadžbe b2x2 + a2y2 = a2b2, odnosno b2x2 — a2y2 = a2b2, gdje su a, b mjerni brojevi poluosi OA, resp. OC (sl. 5, 6). Otada je to svojstvo elipse, odnosno hiperbole, ostalo kao najomiljelije definiciono svojstvo za obrađivanje tih dviju čunosječnica, te se uzima i u srednjim školama. Oblik
x2/a2± y2/b2 = 1
javlja se prvi put u djelu G. Lamé, Examen des différentes méthodes employées pour résoudre les problèmes de géométrie (Pariz 1818).
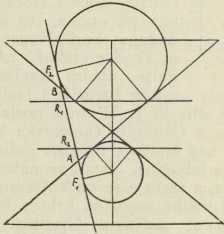
Svezu te definicije s onim iskonskim izvođenjem čunosječnica kao ravnih presjeka stošca otkrio je g. 1822 belgijski matematičar P. Dandelin. Ako naime rotacioni stožac presiječemo nekom ravninom u čunosječnici, pak odredimo one stošcu upisane kugle, koje diraju tu presječnu ravninu, tada su dirališta upravo fokusi presječne čunosječnice (sl. 7, 8, 9), jer se vrlo lako izvede, da je zbroj provodnica kod elipse, odnosno razlika kod hiperbole, konstantna. No iz istih prostornih figura možemo izvesti i Papovo svojstvo, spomenuto u točki 3. Svaka od onih upisanih kugala dira naime stožac uzduž kružnice, kojoj je ravnina usporedna s bazom stošca, a presječnica te ravnine s ravninom čunosječnice upravo je ravnalica te krivulje (u slikama idu te ravnalice točkama R1, R2, R okomito na ravninu papira).
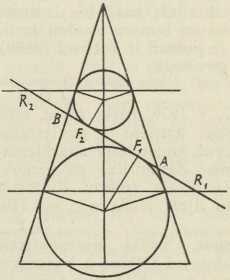 Sl. 7.
Sl. 7.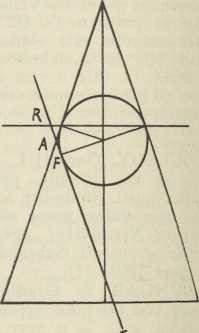 Sl. 8.
Sl. 8.6. Sve dosadašnje definicije čunosječnica bile su više ili manje očito u svezi sa stošcem, na kojem se one nalaze kao presjeci. Sada ćemo dati još dvije definicije, koje nemaju nikakve sveze sa stošcem, nego su čisto planimetrijske. Prvu od njih dao je J. Steiner u djelu Systematische Entwickelung der Abhängigkeit geometrischer Gestalten von einander (Berlin 1832), te glasi: Čunosječnica je geometrijsko mjesto sjecišta korespondentnih pravaca dvaju projektivnih pramena (sl. 10). To je shvaćanje t. zv. projektivne geometrije (v.), koju je osnovao V. Poncelet svojim djelom Traité des propriétés projectives des figures (Pariz 1822), gdje projektivno srodstvo ili projektivitet (v.) fundira s pomoću centralne projekcije, dok ga Steiner, nadovezujući na Möbiusa, definira s pomoću jednakosti dvoomjera (v.) korespondentnih četveraca.
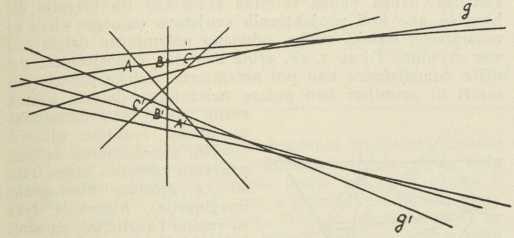
U projektivnoj geometriji može se čunosječnica definirati i kao anvelopa svojih tangenata, pak je u tom smislu ona generirana s pomoću dva projektivna niza g (A, B, C,...), g’(A’,B’,C’,...), sl. 11 To je izvođenje dualno onome s pomoću dva projektivna pramena, a princip dualiteta, koji je za projektivnu geometriju, dakle i za teoriju čunosječnica, od fundamentalne važnosti, spoznao je prvi Poncelet dok ga je Gergonne 1827—29 utvrdio općeno, a Möbius 1827 i Plücker 1830 dadoše mu najopćeniji oblik.
 Sl. 9.
Sl. 9.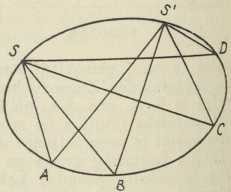 Sl. 10.
Sl. 10.7. Druga projektivna definicija čunosječnica osniva se na pojmu korelacije, koji je uveo u nauku A. F. Möbius u djelu Der barycentrische Calcul (Leipzig 1827), a koji se sastoji u ovome: Između dviju ravnina postoji srodstvo, po kojemu je a) svakoj točki jedne ravnine pridružen posve određeni pravac druge i obrnuto, te b) točkama nekog pravca jedne pridruženi su pravci nekog pramena druge. Ako te dvije ravnine položimo jednu na drugu, tada možemo pitati, postoji li točka u ravnini, koja leži na svom korelativno korespondentnom pravcu i dualno, postoji li pravac, koji ide svojom korelativno korespondentnom točkom. Na osnovu toga definirao je Chr. v. Staudt u djelu Geometrie der Lage (Nürnberg (1847) čunosječnicu kao skup točaka, koje imaju to svojstvo, da su incidentne sa svojim korelativno korespondentnim pravcima, resp. kao anvelopu pravaca, koji su incidentni sa svojim korelativno korespondentnim točkama (incidenca točke i pravca znači, da točka leži na pravcu, odnosno, da pravac ide točkom). Općeno su te dvije čunosječnice za zadanu kolokalnu (t. j. u istoj ravnini) korelaciju međusobno različite; ako su istovjetne, tada se korelacija zove involutorna ili polaritet.
Ovom je definicijom postignut vrhunac u geometrijskom izvođenju čunosječnica, pak nam sada preostaje još da prikažemo uglavnom samu teoriju čunosječnica. Ova nam se očituje u dva oblika: sintetičkom i analitičkom. U prethodnom prikazu različitih definicija čunosječnica (u kojem je sadržan već i dobar dio povijesnog razvoja teorije čunosječnica) uglavnom smo postupali sintetički, čisto geometrijski, pak ćemo zato teoriju čunosječnica dati u analitičkoj metodi.
 Sl. 11.
Sl. 11.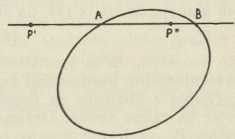 Sl. 12.
Sl. 12.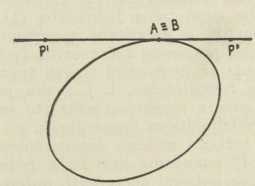 Sl. 13.
Sl. 13.Da bi se obuhvatila sva svojstva čunosječnica, treba raditi s općenim projektivnim koordinatama x1 : x2 : x3 u ravnini (→ koordinate), jer one u jednu ruku zbog svoje homogenosti omogućuju savršenu simetričnost formula, a u drugu ruku dopuštaju specijalizaciju u afine i ekviformne koordinate (→ koordinate). S pomoću projektivnih koordinata moći će se analitički opisati ili izraziti sva t. zv. projektivna svojstva čunosječnica, t. j. svojstva, koja ostaju uščuvana, ako čunosječnicu projiciramo centralno na neku drugu ravninu; afine koordinate prirodni su analitički aparat za obrađivanje svih onih svojstava čunosječnica, koja ostaju nepromijenjena kod paralelnog projiciranja, dakle svojstva, koja se osnivaju na paralelizmu, dok su ekviformne koordinate (to su obične Kartezijeve koordinate) adekvatni instrument za istraživanje svojstava, koja su u bitnoj svezi s ortogonalitetom ili okomitošću u ravnini.
Kakogod definirali čunosječnice (a osobito to vrijedi za definicije 6 i 7), uvijek će njihova jednadžba u projektivnim koordinatama glasiti
f(x,x)≡a11x12 + a22x22 + a33x32 + 2a23x2x3 + (1)
+ 2a31x3x1 + 2a12x1x2=0,
gdje su veličine aik poznati realni brojevi, a x1, x2, x3 varijabilne koordinate kurentne točke P na čunosječnici. Ta je jednadžba 2. stupnja u tim kordinatama, pak će zato sa svakom linearnom jednadžbom
c1x1 + c2x2 + c3x3=0, (2)
gdje su ci poznate konstante, imati dva rješenja zajednička. No ta linearna jednadžba geometrijski znači neki pravac, pak će ona dva rješenja biti koordinate sjecišta čunosječnice i toga pravca. Dakle svaki pravac ravnine siječe čunosječnicu u dvije točke, a zbog toga se svojstva čunosječnice zovu krivulje 2. reda.
U jednadžbi (1) dolazi 6 konstanata, ali ih je samo 5 bitnih, jer s jednom od njih možemo cijelu jednadžbu razdijeliti, pak zadati samo njihove omjere. Odatle slijedi, da je krivulja 2. reda određena sa svojih 5 točaka, što je našao već Papo čisto geometrijskim putem. S pomoću same jednadžbe (1) može se dokazati osobito važni Pascalov stavak: ako je šesterovrh upisan u krivulju 2. reda, tada sjecišta triju parova suprotnih stranica leže na jednom istom pravcu, koji se zove Pascalov pravac (B. Pascal, Essay pour les Coniques, Pariz 1640). Njegov dualni stavak o opisanom šesterostranu našao je Ch. Brianchon g. 1810.
Na osnovu jednadžbe (1) dade se provesti vrlo pregledno i klasifikacija čunosječnica, t. j. određivanje svih mogućih vrsta njihovih, uključivo i one, gdje čunosječnica degenerira raspadajući se u dva pravca. Te se vrsti mogu uostalom naći i s pomoću onog iskonskog postanka tih krivulja, naime s pomoću sječenja čunja ravninom.
Za čitavo daljnje analitičko ispitivanje čunosječnica od osnovne je važnosti postupak, koji je uveo F. Joachimsthal g. 1846, a sastoji se u ovome: ako su P'(x1' : x2' : x3'), P" (x1″ : x2″ : x3″) dvije točke ravnine, tada tri broja x1'—λx1″, x2'—λx2″, x3'—λx3″, gdje je λ neki po volji odabrani broj, znače koordinate neke točke Q na pravcu P'P", pak varirajući taj broj λ (koji se zove parametar, ali nema nikakve sveze s parametrom iz točke 2) na sve moguće načine dobivamo sve točke pravca P'P". Želimo li sada, da točka Q leži na čunosječnici (1), morat će po općenom načelu analitičke geometrije koordinate te točke zadovoljavati jednadžbu te krivulje, t. j. mora biti f(x'—λx″, x'—λx") ≡ a11(x1'—λx1″)2+.....
+ 2a12(x1' — λx1″) (x2'— λx2") = 0.
Ako to razvijemo i sredimo po potencijama od λ, dobivamo jednadžbu
f(x', x')—2λ ∙ f(x', x") + λ2 ∙ f(x", x")=0,b (3)
gdje su f(x', x'), f(x", x") izrazi kao u (1) samo pisani za koordinate x1' : x2' : x3,' resp. x1″ : x2" : x3")mjesto za koordinate x1 : x2 : x3, dok je veličina f(x', x") dana formulom f( x',x")≡a11x1'x1″ + a22x2'x2" + a33x3'x3" + a23(x2'x3″ + x3'x2") +a31(x3'x1″ + x1'x3") + a12(x1'x2" + x2'x1"). (4)
Taj se izraz f(x', x") zove polarna forma kvadratne forme f(x, x) (→ forme). Rješenja kvadratne jednadžbe (3) glase
λ1, 2 = f (x', x'') ± √ f (x', x'')2 − f (x', x') : f (x'', x'') /f (x'', x'') (5)
pak su točke A(x1'—λ1x1" : x2'—λ1x2" : x3'—λ1x3"), B(x1'— — λ2x1":x2'—λ2x2″:x3'—λ2x3″) sjecišta čunosječnice (1) s pravcem P'P".
Ali nije sva važnost u tome, što smo odredili ta sjecišta, nego se iz formule (5) dadu izvući sva glavna projektivna svojstva čunosječnica. Ako naime točke P',P" udesimo tako, da je izraz pod korijenom = 0, tada je λ2 = λ1, dakle B≡A, t. j. pravac P'P" je tangenta čunosječnice (sl. 13), dok je do sada bila samo sekanta.
 Sl. 14.
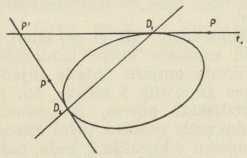
Sl. 14.Uzmemo li dakle točku P' čvrstom, a točku P" variramo i kao takvu označimo jednostavno sa P, značit će nam jednadžba
f(x', x)2—f(x', x') ∙ f(x, x) = 0 (6) geometrijsko mjesto svih onih točaka P(x1 : x2 : x3) ravnine, koje imaju to svojstvo, da je pravac P'P tangenta od (1). No geometrijski zor kaže nam, da se to geometrijsko mjesto sastoji od dva pravca, naime dvije tangente, povučene iz točke P' na čunosječnicu (sl. 14), a to nam potvrđuje i jednadžba (6), koja nam te dvije tangente analitički predočuje i zbog čega se ta jednadžba mora dati rastaviti u dvije linearne jednadžbe oblika (2). Jednadžba (6) dakle znači skupnu jednadžbu para tangenata iz točke P' na čunosječnicu (1). Našli smo dakle važno svojstvo, da se iz svake točke ravnine daju na čunosječnicu povući dvije tangente; zbog toga se čunosječnice zovu krivuljama 2. razreda, a jer je za te krivulje razred jednak redu, zovu se skupno krivuljama 2. stupnja. — Ako je točka P' specijalno na samoj čunosječnici, dakle f(x', x') = 0, tada se jednadžba (6) steže na f(x',x)2 = 0, a ta znači dvostruki pravac f(x', x) = 0, (7) koji predočuje tangentu u točki P' krivulje (1). Pri tom je dakako f(x', x) polarna forma od f(x, x), građena prema tipu (4).
 Sl. 15.
Sl. 15.Daljna je vrlo važna posljedica formule (5) ova: u elementima analitičke geometrije pokazuje se, da za λ2 = — λ1 točke P',P",A,B moraju biti četiri harmoničke točke (→ harmonitet) i obrnuto. No u tom slučaju izlazi iz (5), da je f(x', x") = 0.(8) Dvije točke P', P", koje imaju to svojstvo, da sa sjecištima A, B svoje spojnice P'P" i čunosječnice čine harmonički četverac, zovemo konjugiranim točkama s obzirom na čunosječnicu, pa je (8) analitički uvjet za takve točke. Držimo li opet točku P' čvrstom, a točku P" variramo i zato je označimo sa P, bit će jednadžbom f(x',x) = 0 (9) predočeno geometrijsko mjesto točaka P, koje su sve konjugirane s jednom istom točkom P' s obzirom na čunosječnicu (1). To je geometrijsko mjesto pravac (jer je jednadžba (9) linearna u kurentnim koordinatama x1, x2, x3), te se zove polara točke P' s obzirom na čunosječnicu, a točka P' je njezin pol. (Treba dobro razlikovati jednadžbu (7) od jednadžbe (9): ona znači tangentu u točki P', koja leži na čunosječnici, a ova polaru točke P', koja ne leži na čunosječnici; ako P' i u ovom slučaju bude na čunosječnici, tada polara prelazi u tangentu, i tada su one dvije jednadžbe ne samo formalno, nego i geometrijski istovjetne). Sada se može vrlo lako pokazati, da je polara točke P' spojnica dirališta onih dviju tangenata, koje se daju povući na čunosječnicu iz te točke (t. zv. dodirna sekanta), sl. 14. To je početak važne partije teorije čunosječnica, naime teorije polariteta s obzirom na zadanu čunosječnicu; tu su najvažniji pojmovi: konjugirane polare i polarni trovrh. Ovaj je važan za to, jer uzmemo li, da je koordinatni trovrh polaran s obzirom na čunosječnicu, tada se jednadžba ove reducira na normalni ili kanonski oblik
a11x12 + a22x22 + a33x32= 0,
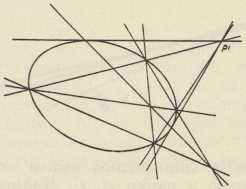
u kojem dolaze samo kvadratni članovi. A taj je oblik mnogo zgodniji za istraživanje nego puna jednadžba (1). Od mnogih stavaka iz te partije o polaritetu spomenut ćemo samo ova dva: 1. Ako vrsi potpunog četverovrha (v.) leže na nekoj čunosječnici, tada je diagonalni trovrh toga četverovrha polarni trovrh te čunosječnice, t. j. svaka je stranica diagonalnog trovrha polara suprotnog vrha (to se svojstvo dade vrlo zgodno upotrijebiti za konstrukciju polare i tangenata za zadanu točku i zadanu čunosječnicu s pomoću samog ravnala: iz P' povučemo bilo koje dvije sekante i t. d., sl. 15); 2. ako je potpuni četverovrh upisan u čunosječnicu, tada svaki pravac ravnine siječe tri para njegovih stranica u tri para točaka neke involucije (v.) točaka na tom pravcu, kojoj su dvostruke točke sjecišta tog pravca i čunosječnice (Desarguesov stavak). U tom polaritetu imamo jedan primjer korelacije, s pomoću koje smo dali definiciju 7 čunosječnica; jer tu doista svakoj točki ravnine odgovara posve određen pravac — njegova polara, a svakom pravcu posve određena točka — njegov pol. Taj je polaritet upravo onaj specijalni slučaj korelacije, koji smo na citiranom mjestu pod tim imenom spomenuli.
To je u glavnim obrisima projektivna teorija čunosječnica; druga velika skupina svojstava tih krivulja dobiva se, ako kod projektivnih svojstava uzmemo obzir na neizmjerno daleke točke, odnosno neizmjerno daleki pravac ravnine. To su t. zv. afina svojstva čunosječnica: središte čunosječnice kao pol neizmjerno daleka pravca, diametri ili promjeri kao polare neizmjerno dalekih točaka, zatim afine vrsti čunosječnica prema realitetu njihovih sjecišta s neizmjerno dalekim pravcem ravnine: elipsa (ako su ta sjecišta konjugirano imaginarna), hiperbola (ako su realna i različita), parabola (ako padaju zajedno; tu je dakle neizmjerno daleki pravac ravnine tangenta parabole); onda asimptote kao diametri, koji idu tim neizmjerno dalekim točkama čunosječnice i konjugirani dijametri kao korespondentni pravci u involuciji, kojoj su asimptote dvostruki pravci.
Napokon se još dobije treća skupina t. zv. ekviformnih ili metričkih svojstava čunosječnica, ako uzmemo u obzir još i ortogonalitet u ravnini: osi čunosječnica kao među sobom okomiti konjugirani diametri, fokusi kao sjecišta tangenata povučenih na čunosječnicu iz apsolutnih točaka (v.) ravnine (Plücker), ekscentricitet linearni i numerički, ravnalice kao polare fokusa, osna jednadžba čunosječnica, kako smo je uzeli kod definicije 5, normale, oskulacione kružnice i t. d.
Sve ovo, što smo do sada govorili, tiče se pojedinačnih čunosječnica, a sada dolazi na red partija o dvjema čunosječnicama, uzetima istodobno; tu imamo najprije određivanje njihovih zajedničkih točaka i stavak, da dvije čunosječnice imaju 4 sjecišta, zatim imamo pramen čunosječnica kao skup svih ∞1 čunosječnica kroz ta 4 sjecišta i čitavu veliku teoriju toga pramena; zatim sličnost čunosječnica pa konfokalne čunosječnice i na tom fundirane t. zv. eliptične, odnosno parabolične koordinate u ravnini; onda mreže čunosječnica i t. d.
Posebno poglavlje nauke o čunosječnicama čini izračunavanje duljine lukova čunosječnica i površine likova, omeđenih tim krivuljama, to su t. zv. rektifikacija i kvadratura čunosječnica.
Na koncu još ćemo istaknuti, da čunosječnice nisu samo predmet teoretskih matematičkih proučavanja, nego imaju i izvanredno mnogostranu primjenu. To su krivulje, koje se od svih najviše primjenjuju, čak i u najobičnijim prilikama života (osobito elipsa), a onda u obrtu, tehnici, pa u različitim znanostima: mehanici, optici, geografiji, astronomiji te u različnim granama same matematike.
LIT.: Osim djela, koja su navedena u samom članku, važna su još ova: H. Balsam, Apollonius von Perga, 8 Bücher Kegelschnitte, Berlin 1861; F. Hultsch, Pappi Alexandrini collectiones quae supersunt, 3 sv., Berlin 1876—78; J. Majcen, Matematički rad Boškovićev, II. dio, Rad Akademije, knj. 225 Zagreb 1921; F. Dingeldey, Kegelschnitte und Kegelschnittsysteme, Enc. der math. Wiss., sv. III., dio II., 1., Leipzig 1903; Heffter-Koehler, Lehrbuch der analytischen Geometrie, sv. I., Leipzig 1905, 2. izd., Karlsruhe 1927.R. C.