 b)
b)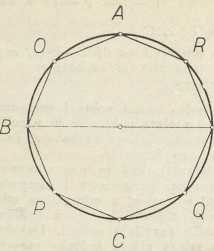 a)
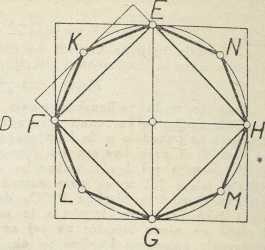
a)EKSHAUSTIJA označuje metodu, kojom su starogrčki matematičari dokazivali geometrijske teoreme, koji se po svojoj naravi ne mogu dokazati elementarno, jer u izravno njihovo dokazivanje ulaze bezkonačni postupci. Metoda e-e neizravan je način dokazivanja (→ dokaz), koji se osniva na ove četiri predpostavke: 1) da za dvie zadane veličine iste vrsti A i B (na pr. dvie dužine ili dva ravna lika ili dva tiela) postoji samo jedna od triju mogućnosti: ili je A veće od B, ili je A manje od B, ili je A jednako B; ako dakle A nije ni veće ni manje od B, mora biti jednako B; 2) ako su zadane tri veličine A, B, C iste vrsti, da postoji uviek jednoznačno određena četvrta geometrijska proporcionala, t. j. veličina X iste vrsti takva, da je A : B = C : X, i to onda, kada se ta veličina ne da konstruirati elementarno; taj postulat o postojanju četvrte geometrijske proporcionale nisu grčki matematičari izričito izrekli, ali su se njime stalno služili, pri čemu on ima u njihovu zaključivanju ono mjesto, što ga danas zauzima pojam neprekinutosti jednoga podpunoga sustava istovrstnih veličina; 3) na važnom teoremu 1. knj. X. Euklidovih Elemenata, za koji se s velikom vjerojatnosti drži da u svojoj biti (a možda i obliku) potječe od velikoga matematičara Platonova vremena Eudoksa, a koji glasi: ako su zadane dvie nejednake veličine iste vrste, pa ako se od veće oduzme veličina veća od njene polovine ili jednaka njoj, a od ostatka isto tako veličina veća od polovine ili jednaka njoj, i ako se to dalje nastavlja, preostat će veličina, koja je manja nego manja od zadanih veličina. Da se uvidi bit metode e-e navest ćemo Euklidov dokaz teorema XII, 2, da se ploštine dvaju krugova odnose kao kvadrati njihovih promjera, za koji se zna, da ga je izrekao i na neki način i dokazao Hipokrat s Hija, no strogo da ga je dokazao tek Eudokso. Neka su ABCD i EFGH zadani krugovi, K1 i K2 njihove ploštine; treba pokazati, da vriedi razmjer K1: K2= BD2: FH2. Uzmimo, da nije tako; tada bi prema postulatu o postojanju četvrte proporcionale morao postojati neki lik u ravnini, kojega bi ploština P zadovoljavala taj razmjer, tako da bi bilo K1: P = BD2: FH2.Kako je P različito od K2, to je prema 1) K2>P ili K2<P. Neka je najprije K2>P, i razmotrimo posljedice, do kojih to vodi. Upišimo u tu svrhu u krug K2 kvadrat EFGH. On je veći od polovine kruga K2, jer je jednak polovini kvadrata opisana oko kružnice K2 (kako se razabire iz slike b), a ta je polovina veća od polukruga FEH; ako se dakle oduzme od kruga K2 kvadrat EFGH, oduzela se time od njega veličina veća od 1/2 K2, a preostala su četiri kružna odsječka nad stranicama toga kvadrata. Ako u K2 upišemo pravilni osmerokut EKFLGMHN time, da razpolovimo lukove EF, FG, GH i HE točkama K, L, M i N i povučemo tetive EK, KF, FL,..., HN i NE, to je svaki od trokuta EKF, FLG, GMH i HNE, koji time nastaju nad stranicama kvadrata EFGH, veći od polovine kružnoga odsječka nad istom stranicom, kako se opet vidi promatranjem pravokutnika nad tetivama EF, FG, GH i HE; tako je na pr. trokut EKF polovina pravokutnika nad tetivom EF (sl. b), a kružni odsječak nad tom istom tetivom veći je od trokuta. Ako dakle oduzmemo od preostalih četiriju odsječaka kruga zbroj tako nastalih trokuta, oduzeli smo od njih veličinu veću od polovine zbroja tih odsječaka, dok je preostalo osam kružnih odsječaka nad stranicama osmerokuta. Ako se taj postupak nastavi dalje, dakle ako se prieđe od pravilna upisana osmerokuta na pravilne upisane višekute sa 16, 32,... stranica, umanjivat će se zbroj kružnih odsječaka, što preostaju svaki put nakon oduzimanja tih višekuta sa sve većim brojem stranica od kruga K2, jer se pri svakom koraku oduzima više od polovine zbroja odsječaka dobivenih pri pređašnjem koraku. Ako se dakle postupak nastavi dovoljno daleko, doći će se i do pravilna višekuta V2 takva, da će zbroj kružnih odsječaka, što ih on određuje u K2, prema teoremu X, I, iznositi manje od veličine K2 — P, za koju ploština K2 premašuje P. No kako je zbroj tih odsječaka jednak razlici K2—V2, to je K2—P>K2—V2, t. j. P<V2. Došli smo dakle do pravilna upisana višekuta V2 s tolikim brojem stranica, da on svojom ploštinom premašuje veličinu P. Konstruirajmo sada i u krugu K1 pravilni upisani višekut V1 = AOBPCQDR s jednakim brojem stranica, koji je sličan višekutu V2. Za takve višekute vriedi (Elem. XII, 1), da im se ploštine odnose kao kvadrati promjera krugova, u koji su upisani, da je dakle V1: V2 = BD2: FH2; ali jer je i K1: P = BD2: FH2, to je i K1 : P =V1 : V2 ili K1: V1 = P : V2. No iz slike se vidi, da je ploština K1>V1; dakle je na temelju zadnjega razmjera i P>V2, a moralo bi biti prema gore navedenom rezultatu P < V2. Kako smo timedošli do proturječja, nemoguće je, da je K2>P. No slično se dokazuje, da i predpostavka K2>P vodi do proturječja, tako da se odatle zaključuje, da može samo vriediti P = K2, t. j. K1: K2 = BD2: FH2, a to je tvrdnja, koju je trebalo dokazati.
Tom metodom dokazuje Euklid još i teorem, da se trostrane piramide jednakih visina odnose kao osnovke (teorem X, 5), da je obujam uzpravna stožca jednak jednoj trećini obujma uzpravna valjka, koji ima istu osnovku i jednaku visinu (X, 10), da se stožci (kao i valjci) jednakih visina odnose kao njihove osnovke (X, 11), da se slični stožci (kao i valjci) odnose kao treće potencije promjera njihovih osnovaka (X, 12), da se napokon obujmi kugala odnose kao treće potencije njihovih promjera (X, 18) I Arhimed se obilno služi tom metodom dokazivanja; njom dokazuje na pr. znameniti svoj teorem, da je oplošje kugle četiri puta tako veliko kao ploština najvećega njena kruga (O = 4r2π), i da je obujam kugle četiri puta tako velik kao obujam stožca, kome je osnovka jednaka ploštini najvećega kuglina kruga, a visina jednaka polumjeru kugle (V = 4/3 r3π).
Iz prije navedenog primjera, a i iz svih drugih izlazi, da dokazivanje metodom e-e teče po uzoru svakoga neizravnog dokaza; osim toga, da ta metoda predpostavlja, da je postojanje veličina, o kojima se razpravlja, već osigurano, i da je teorem, o kome se radi, već poznat; metodom se e-e taj teorem samo utvrđuje strogim zaključivanjem. Osobitost te metode stoji u jednu ruku u uvođenju onoga slieda pomoćnih upisanih (ili i opisanih) likova (ili uobće geometrijskih tvorevina), s pomoću kojega se dokazuje na pr. u gornjem slučaju, da ima uviek jedan višekut slieda, koji premašuje veličinu P uvedenu u dokaz samo neizravnim načinom dokazivanja; u drugu ruku u činjenici, da je taj slied konačan, da se zaustavljamo u njemu, čim smo došli do višekuta, koji zadovoljava uvjet V₂ > P. Ta je okolnost napose važna, jer obilježuje gledište konačnosti (finitnosti) starogrčkih matematičara, kojega su se oni dosljedno držali. Njime su oni uklonili iz geometrijskih razmatranja i uvođenje pojma bezkonačno velikoga (v.), koji bi ušao u razmatranje, da se broj stranica višekuta uvećavao bez kraja, a i pojma bezkonačno maloga, koji bi se javio time, što se razlika između kruga i višekuta s brojem stranica, što raste u bezkonačnost, neprestano umanjuje i teži nuli. Time su oni izbjegli težkoće i opasnosti, što se javljaju pri upotrebi bezkonačnih postupaka, o kojima se živo razpravljalo u grčkoj filozofiji i matematici u 5. i 4. st. pr. Kr. (→ Zenon).
Premda je u svim slučajevima primjena te metode dokazivanja u bitnosti ista, nema viesti iz starine, da bi je itko formulirao kao obće načelo, nego je Euklid i Arhimed svagda nanovo izvode. Tek je u 17. st. Luca Valerio prvi izlučio iz postupaka Euklida i Arhimeda bit toga dokazivanja i izrekao je u svome De centro gravitatis solidorum (O težištu čvrstih tjelesa, Rim 1604) u teoremu: ako su zadane dvie veličine iste vrste A i B, pa ako su veličine iste vrste A₁ i B₁ takve, da se A₁ može razlikovati od A, a B₁ od B za kakvugod zadanu veličinu, ostajući obje uviek ili manje od A, dotično B, ili veće, ako nadalje veličine A₁ i B₁ stoje uviek u stalnom omjeru C : D, isti će omjer vriediti i za veličine A i B, t. j. iz A₁: B₁ = C : D izlazi A : B = C : D. Tim je teoremom napokon unesena u postupak starih matematičara preglednost, jednolikost i obćenitost, a uveden je obćenito i onaj moment, koji će za dalji razvoj biti odlučan, naime da veličine A₁ i B₁ mogu doći veličinama A i B bliže od svakoga zadanog iznosa, dakle po volji blizu. Dalji je korak u toj teoriji učinio Gregorius a Sto. Vincentio u djelu Opus geometricum quadraturae circuli et sectionum coni (Geometrijsko izvođenje kvadrature kruga i presjeka stožca, Antwerpen 1647), u kojem on traži »nova umieća i nove metode«, kojima bi se doskočilo »nedostatcima« grčke geometrije, i u suprotnosti s osnovnom misli staroga grčkog dokazivanja prelazi od konačnoga slieda upisanih ili opisanih likova na bezkonačan slied uviek novih likova, a uz neizravno dokazivanje po uzoru Arhimedovu uvodi već i izravno razmatranje na bezkonačnim sliedovima likova. Od njega potječe i naziv ekshaustija (od lat. exhaurire »izcrpsti«) za ono sve podpunije izpunjavanje nutarnjosti kružnice s višekutima, koji imaju sve veći broj stranica, tako da razlika između ploštine višekuta s dovoljno velikim brojem stranica i ploštine kruga može postati po volji malena. Na njega je možda utjecao njegov zemljak S. Stevin, koji se već služi bez daljeg dokazivanja zaključkom, da su dvie veličine jednake, ako se razlikuju za veličinu po volji malu. Napokon je A. Tacquet jasno iztakao onaj pojam, koji čini bit toga novog shvaćanja i prirodno se javlja, ako se napusti gledište konačnosti grčkih matematičara; to je pojam graničnog približavanja i granične vriednosti (v.). U svojim Elementa geometriae planae ac solidae (Počela geometrije u ravnini i prostoru, Antwerpen 1654) definira on »teženje«, ili po današnjem »konvergiranje«, jednog slieda veličina; za ploštine upisanih ili opisanih likova kaže da teže ploštini zadanoga čvrstog lika kao granici, ako se od nje mogu napokon razlikovati za veličinu po volji malu. S pomoću tog pojma izriče on tada i teorem Valerijev u novom, jednostavnom obliku, koji u današnjoj oznaci glasi: ako su An i Bn ploštine upisanih ili opisanih likova, na pr. pravilnih n-terokuta, i ako s lim (lat. limes »granica«) označimo graničnu vriednost, kojoj oni teže, kad broj n stranica višekuta raste bez kraja tako, da je lim An= A, lim Bₙ = B, pa ako za svaki broj stranica n vriedi An : Bn = C : D, tada je i A : B = C : D. Nezavisno od njega uvodi pojam granične vriednosti i P. Mengoli (1650) i primjenjuje ga na bezkonačne redove.
Tako su se matematičari novijega vremena, nestrpljivi u nastojanju, da što življe i uspješnije prošire područje matematičkog iztraživanja i njegovih primjena, odtisnuli od stajališta konačnosti starih Grka i njegove sigurnosti i zaplovili na pučinu bezkonačnosti, punu opasnosti, te sviestno udarili putem izravnoga graničnog prielaza, koji ih je vodio u jednu ruku do bezkonačnih sliedova i redova (Torricelli, Gregorije, Mengoli, Tacquet, Wallis, Gregory), a u drugu ruku do pripremanja pojma integrala (još prije Kepler, pa Cavalieri, Pascal, Wallis, Barrow). Što se pri tom shvaćanju novijih matematičara izgubilo na strogosti izvoda, naknadilo se obiljem novih rezultata dobivenih izravnim postupkom graničnoga prielaza. No tako nastale nove metode dobile su sigurnu podlogu tek početkom 19. st., kad je A. L. Cauchy izradio jasnu i strogu teoriju graničnih postupaka. Tim su se postupcima izvanredno obogatila sredstva matematičkog iztraživanja, jer je bila dana mogućnost neograničenog uvođenja novih matematičkih tvorevina kao rezultat izpravno provedenih graničnih prielaza; pritom nije trebalo tek predpostavljati postojanje tih novih tvorevina, nego je ono izlazilo iz obćih teorema te teorije. Ali previranje, koje je time nastalo u shvaćanju osnova više analize, tako je duboko sezalo u njene osnove, da se razvoj završio tek u drugoj polovini 19. st. izgradnjom stroge teorije realnih brojeva (v.). Ž. M.